本文参考labuladong算法笔记[【强化练习】用「分解问题」思维解题 II | labuladong 的算法笔记]

技巧一

类似于判断镜像二叉树、翻转二叉树的问题，一般也可以用分解问题的思路，无非就是把整棵树的问题（原问题）分解成子树之间的问题（子问题）。

100. 相同的树 | 力扣 | LeetCode |

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

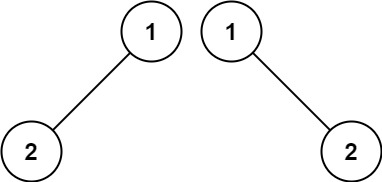
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

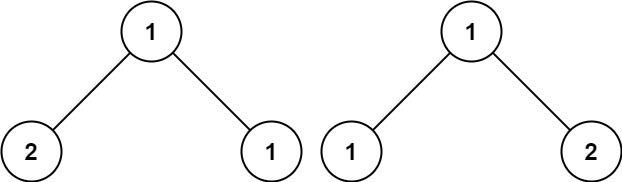
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

• 两棵树上的节点数目都在范围 [0, 100] 内
• -104 <= Node.val <= 104

判断两棵树是否相同，可以分解为判断根节点是否相同，然后判断左右子树的节点是否都相同。

class Solution:# 定义：输入两个根节点，返回以它们为根的两棵二叉树是否相同def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:# 判断一对节点是否相同if p is None and q is None:return Trueif p is None or q is None:return Falseif p.val != q.val:return False# 判断其他节点是否相同return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

101. 对称二叉树 | 力扣 | LeetCode |

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

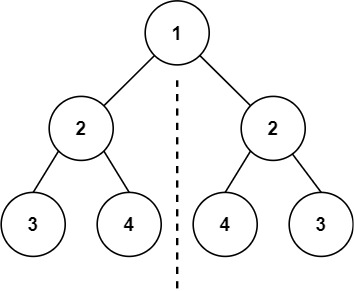
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

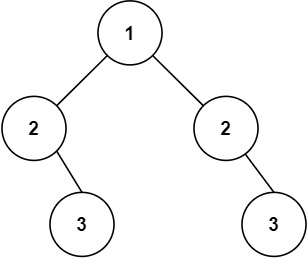
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

这道题有点像 100.相同的树，你可以对比一下两道题的代码，只不过本题不是让你比较两棵树是否相同，而是让你比较两棵子树是否对称。

那么分解问题的思路就很明显了，判断两棵树是否镜像对称，只要判断两棵子树都是镜像对称的就行了。

如果用迭代的方式，可以使用 BFS 层序遍历，把每一层的节点求出来，然后用左右双指针判断每一层是否是对称的。

class Solution:def isSymmetric(self, root: TreeNode) -> bool:if root is None:return True# 检查两棵子树是否对称return self.check(root.left, root.right)# 定义：判断输入的两棵树是否是镜像对称的def check(self, left: TreeNode, right: TreeNode) -> bool:if left is None or right is None:return left == right# 两个根节点需要相同if left.val != right.val:return False# 左右子树也需要镜像对称return self.check(left.right, right.left) and self.check(left.left, right.right)

951. 翻转等价二叉树 | 力扣 | LeetCode |

我们可以为二叉树 T 定义一个 翻转操作 ，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y，我们就称二叉树 X 翻转 等价 于二叉树 Y。

这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是翻转 等价 的函数，则返回 true ，否则返回 false 。

示例 1：

输入：root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
输出：true
解释：我们翻转值为 1，3 以及 5 的三个节点。

示例 2:

输入: root1 = [], root2 = []
输出: true

示例 3:

输入: root1 = [], root2 = [1]
输出: false

提示：

• 每棵树节点数在 [0, 100] 范围内
• 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数

如何分解这个问题呢？原问题是两棵二叉树是否是翻转等价的，只要两棵树的根节点能够匹配，那我们就可以去考察这两个根节点的左右子树（共四棵）是否是翻转等价的。

对子树把翻转和不翻转两种情况全都穷举一遍，只要有一种情况能够匹配，就说明整棵树是翻转等价的，具体实现见代码。

class Solution:# 定义：输入两棵二叉树，判断这两棵二叉树是否是翻转等价的def flipEquiv(self, root1: TreeNode, root2: TreeNode) -> bool:# 判断 root1 和 root2 两个节点是否能够匹配if root1 is None and root2 is None:return Trueif root1 is None or root2 is None:return Falseif root1.val != root2.val:return False# 根据函数定义，判断子树是否能够匹配# 不翻转、翻转两种情况满足一种即可算是匹配return (# 不翻转子树self.flipEquiv(root1.left, root2.left) and self.flipEquiv(root1.right, root2.right)) or (# 反转子树self.flipEquiv(root1.left, root2.right) and self.flipEquiv(root1.right, root2.left))

经典 return：同时判断了需要翻转和不需要翻转两种情况！

124. 二叉树中的最大路径和 | 力扣 | LeetCode |

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

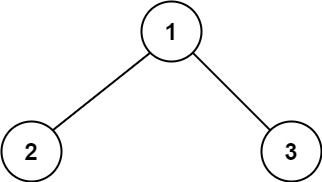
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

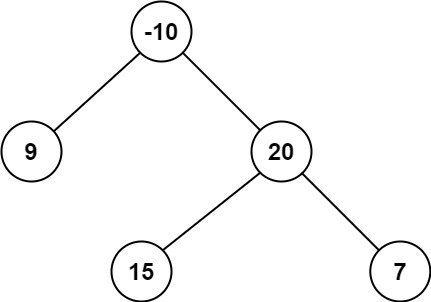
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

这题需要巧用二叉树的后序遍历，可以先去做一下 543. 二叉树的直径 和 366. 寻找二叉树的叶子节点。

oneSideMax 函数和上述几道题中都用到的 maxDepth 函数非常类似，只不过 maxDepth 计算最大深度，oneSideMax 计算「单边」最大路径和：

然后在后序遍历的时候顺便计算题目要求的最大路径和。

class Solution:def __init__(self):self.res = float('-inf')def maxPathSum(self, root: TreeNode) -> int:if root is None:return 0# 计算单边路径和时顺便计算最大路径和self.oneSideMax(root)return self.res# 定义：计算从根节点 root 为起点的最大单边路径和def oneSideMax(self, root: TreeNode) -> int:if root is None:return 0left_max_sum = max(0, self.oneSideMax(root.left))right_max_sum = max(0, self.oneSideMax(root.right))# 后序遍历位置，顺便更新最大路径和path_max_sum = root.val + left_max_sum + right_max_sumself.res = max(self.res, path_max_sum)# 实现函数定义，左右子树的最大单边路径和加上根节点的值# 就是从根节点 root 为起点的最大单边路径和return max(left_max_sum, right_max_sum) + root.val