图论基本术语

图论算法 —— 图论概述-CSDN博客

理论基础 —— 图_依附于顶点v是什么意思-CSDN博客

理论基础 —— 图 —— 图的存储结构_十字链表和链式前向星-CSDN博客

语雀版本

概括：图是计算机中常用的一种存储结构，图论是数学的一个分支，他以图为研究对象，不同情形具有不同的算法。

1 图

图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G=(V,E)，其中 V 是非空有限集合，代表顶点，E 是可以为空的有限集合，代表边。

若顶点 vi 和 vj 间的边没有方向，则称这条边为无向边，用无序偶对 (vi,vj) 表示；若顶点 vi 和 vj 间的边有方向，则称这条边为有向边（弧），用有序偶对 <vi,vj> 表示，其中 vi 称为弧尾，vj 称为弧头。

若图的任意两个顶点之间的边都是无向边，则称该图为无向图；若图的任意两个顶点之间的边都是有向边，则称该图为有向图。

2 基本术语

**简单图：** 不存在顶点到其自身的边，且同一条边不重复出现

**互为邻接点：**无向图中的(vi,vj)，vi和vj互为邻接点

邻接于点vj、邻接自vi、弧<vi,vj>：有向图中的弧<vi,vj>

**无向完全图：**无向图中，任意两个顶点都有边。数量为$ {n\times(n-1)}/2 $

**有向完全图：**有向图中，任意2个顶点都存在方向相反的两条弧。数量为$ {n\times(n-1)} $

**稠密图：**边数接近完全图

**稀疏图：**边数远远少于完全图

**顶点v的度TD(v)：**无向图中，依附于顶点v的边数。对于n个顶点m条边的无向图，所有点的度为2m

顶点v的入度ID(v)：有向图中，弧头为v的弧数量。对于n个顶点m条弧的有向图，所有点的入度为m

顶点v的入度OD(v)：有向图中，弧尾为v的弧数量。对于n个顶点m条弧的有向图，所有点的出度为m

**权：**边的数值。

**网：**带权的图。

**无向图中的路径：**从一个顶点$ v_p $到另一个顶点$ v_q $KaTeX parse error: Expected '}', got 'EOF' at end of input: 的一个顶点序列 ({$ {v_p = v_{i_0}, v_{i_1}, v_{i_2}, …, v_{i_m} = v_q} $KaTeX parse error: Expected 'EOF', got '}' at position 1: }̲)，这个序列代表依次经过的顶点\dots$ v_{ij-1} $和$ v_{ij} $之间都有一条边 $ (v_{ij-1}, v_{ij}) \in E $。也就是说，序列中的每对相邻顶点之间都有一条无向边连接。

**有向图中的路径：**路径是带方向的。

**回路（环）：**起点和终点相同的路径

**简单路径：**顶点不重复出现的路径

**简单回路：**除了起点终点，其他顶点不重复的回路

**路径长度：**非带权图的路径边数，带权图的加权路径边数

子图：对于图 G=(V,E) 和 G’=(V’,E’)，如果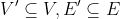，则后者为前者的子图

**连通：**如果顶点vi到vj有路径，则两个顶点连通

**连通图：**无向图中的任意两个顶点连通

连通分量：非连通图的极大连通子图。极大是指包括所有连通的顶点及这些顶点相关联的所有边

**强连通图：**有向图中，任意两个顶点式相互连通的

**强连通分量：**极大强连通子图

生成树：对于连通图G，包含了G中所有顶点的一个极小连通子图。极小指的是子图只有一个顶点入度为0，其余入度为1。

**生成森林：**对于一个非连通图，他由多个连通分量组成，连通分量的生成树构成了该图的生成森林。

3 存储结构

**图的存储常见的有：**邻接矩阵、邻接表、前向星、链式前向星。此外还有不太常见的十字链表和邻接多重表。

邻接矩阵

**对于一个有n个顶点的图，可以用nxn的二维矩阵G来存储边或弧。**

无向图：G[i][j]=1表示点vi和vj互为邻接点。否则为0。

有向图：G[i][j]表示弧的权重。对于不邻接的2个点，用无穷大表示，即2个点的距离无穷大。如下：

优点：查找某条边时，时间复杂度为O(1)。

缺点：空间复杂度高，为O(n^2)。

适用：稠密图。查找某条边的频率高的任务。

邻接表

**用链表来存储图。**

顶点列表：每个顶点都有一个链表或动态数组来存储与它相邻的顶点。
边列表：每条边都作为一个顶点的邻接表项存储起来，并且可以包含附加信息（如权重）。

例子：

A 和 B 的边权重是 2
A 和 C 的边权重是 3
B 和 D 的边权重是 1
C 和 D 的边权重是 4A -> (B, 2) -> (C, 3)
B -> (A, 2) -> (D, 1)
C -> (A, 3) -> (D, 4)
D -> (B, 1) -> (C, 4)

优点：空间节省，为O(n)。遍历某个点的所有出边的效率高。可以处理有重边的图

缺点：查询某条边的效率低。需要变量顶点的所有邻居。对于稠密图，优点不明显。

适用：稀疏图。遍历频繁的任务。

前向星

前面2种的中庸结构。n个数组，每个元素都是一个动态数组，记录每个顶点的出边的邻接点。

int n,m;
vector<int> edge[N];
void init(){cin>>n>>m;for(int i=0;i<m;i++){int x,y;cin>>x>>y;//边所依附的两点编号edge[x].push_back(y);//添边x->yedge[y].push_back(x);//添边y->x}
}

**优点：**资源占用比邻接矩阵低。查询效率比邻接表高。可以处理有重边的图

**缺点：**效率低于邻接矩阵。

**适用：**都可用，能处理处理重边。更适用于稀疏图，因为稠密图用邻接矩阵最方便，且前向星此时对空间的优化不明显。

链式前向星

优化前向星的效率低问题。但增加了操作复杂度，且不好处理重边。

链式前向星通过三个数组来存储图的边，分别是：

**head**** 数组**：记录每个顶点的第一条边的索引。
**to**** 数组**：记录每条边的终点。
**next**** 数组**：记录当前边的下一条边在 to 数组中的位置（链表的指针）。

具体来说：

head[u]：表示顶点 u 的第一条边的编号。
to[i]：表示编号为 i 的边指向的终点顶点。
next[i]：表示编号为 i 的边的下一条边在链表中的位置。

例子：

4个顶点5条边1 -> 2
1 -> 3
2 -> 3
2 -> 4
3 -> 4head[1] = 2
head[2] = 4
head[3] = 5
head[4] = -1  （表示顶点 4 没有出边）to[1] = 2   （1 -> 2）
to[2] = 3   （1 -> 3）
to[3] = 3   （2 -> 3）
to[4] = 4   （2 -> 4）
to[5] = 4   （3 -> 4）next[1] = -1  （表示没有下一条边）
next[2] = 1   （1 -> 2 是 1 -> 3 的下一条边）
next[3] = -1  （没有下一条边）
next[4] = 3   （2 -> 3 是 2 -> 4 的下一条边）
next[5] = -1  （没有下一条边）遍历顶点1：
顶点 1 的第一条边是 head[1] 指向的边 to[2]，表示 1 -> 3；
接着通过 next[2] 找到下一条边 to[1]，表示 1 -> 2。