2.经典规划控制方法-深蓝学院

规划算法

关于规划算法可以参考我的博客
这里说明一下机械臂规划算法的特性以及规划算法的扩展
在这里插入图片描述
任务规划 - 路径规划 - 轨迹优化
过程：路径规划：笛卡尔空间通过IK求解得到关节空间（构型空间c-space），然后通过关节插值生成关节空间轨迹，关节空间通过FK（正运动学）可以得到笛卡尔空间。

其它路径规划算法

• Informed RRT*；BIT •知情RRT*；BIT• Informed RRT*；BIT •知情RRT*；BIT• Informed RRT*；BIT •知情RRT*；BIT• Informed RRT*；BIT •知情RRT*；BIT
• Anytime planner：Should return a valid solution “anytime” later than the initial solution•随时计划器：应该在初始解决方案之后“随时”返回有效的解决方案
• Lazy evaluation： •惰性评估：
• RRT with constraints：Kinematic RRT and Dynamic RRT•带约束的RRT：运动学RRT和动态RRT
• Geometric Method: Medial-Axis RRT：采样特定几何区域。• Geometric Method: Medial-Axis RRT：采样特定几何区域。
Learning for sampling-based planning： Neural RRT; MPNet基于抽样的规划学习：神经RRTMPNet

实践经验

一般来说single-query（树结构算法）比较适合场景变换较快的环境，multi-query（图结构算法）适合静态场景；
树结构算法可以和图结构算法配合，后者作为粗粒度，拓扑关系变换较小的信息，配合树结构算法使用，适合动静结合的场景

Trajectory Generation 轨迹生成

Y: 加入时间，更高维度的连续轨迹（导数）

Point to point trajectory点对点轨迹Point to point trajectory点对点轨迹Point to point trajectory点对点轨迹Point to point trajectory点对点轨迹
• Polynomial •多项式
在这里插入图片描述

• 梯形规划
在这里插入图片描述
而对于多个途径点的规划可以使用Bazier曲线、B样条和多项式曲线

控制算法（以人体按摩为例）

在这里插入图片描述

Force control for massaging按摩力控制Force control for massaging按摩力控制
• 1. The robot is expected to touch human with a constant desired force•1。机器人被期望以恒定的期望力接触人•
• 2. The robot is expected to touch human with a xy trajectory and a time-variant force on z-axis•2。期望机器人以xy轨迹和z轴上的时变力与人接触
• The controller compute a position displacement u to move the robot up or down, then the system force changed accordingly•控制器计算位置位移u，使机器人上下移动，系统力随之变化

在这里插入图片描述
推荐视频教程：PID从理论到实践： https://www.bilibili.com/video/BV1B54y1V7hp

系统建模

Transfer function: 微分方程和laplace 变换，z变换Transfer function: 微分方程和laplace 变换，z变换
状态空间（state space）状态空间（state space）

在这里插入图片描述

Block Diagram

在这里插入图片描述

PID

PD控制器

增加damping ration，减少overshoot
容易受噪声影响

PI

增加系统的阶数，一般稳定性也会随之降低
消除稳态误差

PID

使用关键
需要关注damping ratio，steady-state error
实践中
• 还要关注sensor noise, 适当滤波
• 积分项最好clip，防止非预期的误差累计
• 要注意硬件能力

在这里插入图片描述

调参
Ziegler–Nichols Tuning Rule Based on Step Response of Plant (First Method)

Ziegler–Nichols Tuning Rule Based on Step Response of Plant (Second Method)

控制系统分析

分析方法包括

控制系统的Pole（分母为0）和zero（分子为0）
Characteristic Equation
Pole and root locus
- 系统要求pole 在LHP
- Root locus：通过图形化的方式展示了K从0变化到无穷大时，闭环控制系统极点在复平面上变化的路径

在这里插入图片描述

MPC控制器

可以参考博客
在这里插入图片描述

系统运行图例和优化问题构建和求解流程
在这里插入图片描述
推荐DR_CAN 的MPC视频

实现案例

轨迹跟踪
轨迹优化
Problem setting: replay human demo trajectory, with object-centric and nonlinear mapping、
Reference Trajectory w: recorded human motion data for end-effector
Model: robot kinematic model with speed and workspace limit

Need to deal with speed and workspace constraints, as well as singularity (manipulability)
Predicted Trajectory: predicted state with robot model and constraints
Final output: optimized offline trajectory (end-effector) for robot

力控-导纳控制

T:通过期望力来调整位置
• 通过位置控制来实现追踪期望力

导纳控制是改变期望位置来顺应外力，外力往自己这边顶，那自己的期望位置就往后缩，最后还是尽可能到达改变后的期望位置，只不过这个期望位置相比最初是做了让步的，是位置环控制。

• M，D，K分别代表了惯性特性、阻尼特性和刚度特性
比如推门，需要
在这里插入图片描述
PD控制器
• 根据导纳模型计算𝑥 𝑑
• 通过PD控制追踪𝑥 𝑑

笛卡尔空间力控实现：
• 可以通过关节力矩传感器估计末端力
• 也可以通过末端力传感器实现（后者有一定成本，可靠性更高）

力控-阻抗控制

阻抗控制直接控制力矩来达到期望力

阻抗控制是期望位置不变，根据外力来改变自己的力，外力越大，自己输出的力就越小，最后就算没到期望位置也无所谓，反正自己的力小了，没有跟外力硬碰硬，是力环控制。

对比

阻抗vs导纳（一般来说）：
• 阻抗响应和精度更好，导纳更加柔顺
• 阻抗控制输出力，导纳控制输出位置
• 一般来说，阻抗适合刚性环境，导纳适合柔性环境
• 两者都是基于质量-阻尼-弹簧的系统来实现位置和力的相对关系

操作与抓取的传统方法

历史
在这里插入图片描述

 从manipulation到grasping
• Grasping是manipulation的子集
• 目前很多研究都是基于静态场景的grasping
 Grasping：
•通过在一组接触点施加力和扭矩来抑制物体的运动

Challenge

被抓取的物体通常难以准确建模，因此接触模型往往存在许多假设。
抓取的末端准确位姿难以确定；
抓取的采样和优化是高维问题，求解不容易。

basic

contact

Point Contact
• Frictionless：只考虑法向力
• Friction：法向力和摩擦力

Friction cone： the vector space of all possible/admissible forces a point can
apply due to friction (w/o slipping)

Soft Contact or Patch Contact

wrench

简单的说：force and torque
对于第i个contact point，wrench表达为w_i (d_i是接触点到COM的向量)
Grasp Wrench Space：the set of all possible wrenches that can be applied to an object through admissible forces at k contact points

Evaluation

Patch Contact: cost function is just reward for all of the points in the point cloud, based on how aligned their normal is to the x-axis of the gripper ,
希望接触夹爪与接触点云的面法线对齐

在这里插入图片描述
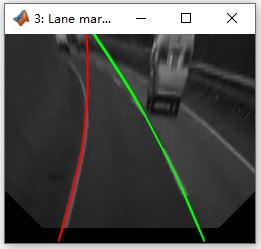
x-y平面抓取，夹爪能够对齐（如图中抓取小刀的红色矩形），并且希望靠近中心，越靠近得分越高。

Force Closure

力封闭指这样一种状态，即如果一个物体因一组施加在物体表面的静态约束而不能发生任何位姿的改变，而这组静态约束完全由于机器人的手指施加在物体接触点处的力螺旋决定，那么就称这种状态为力封闭状态，同时称这组抓取为力封闭抓取。

if the composite wrench cone contains the entire wrench space,so that any external wrench w on the body can be balanced by contact forces 𝑓𝑖 .
处于力平衡的状态
在这里插入图片描述

Grasp Wrench Space
在这里插入图片描述

Grasp Wrench Hull

在这里插入图片描述

在这里插入图片描述

这部分可以参考Fundamentals of Grasping和现代机器人学弟12章

Computing:
 计算每个contact point的力和力矩
 假设2D场景
 计算force cone，wrench space
 原点是否在内

Force closure quality measure example:
 radius of largest ball (in 6D) that is centered at origin and contained within the Grasp Wrench Hull
 Magnitude of smallest external wrench that pushes grasp to its limits
在这里插入图片描述

Form Closure

相对于力闭合更严格
Form closure of a body
• is achieved if a set of stationary constraints prevents all motion of the body.
• If these constraints are provided by robot fingers, we call this a form-closure grasp.
• 4 contact points for 2D; 7 contact points for 6D

The Quality of a Form-Closure Grasp

Eval计算过程
• 构建每个contact point的关系
• 通过linear prog计算k

计算案例：
F为一个列向量，由j个接触力旋量组成的矩阵 (n x j)维，对于平面物体n=3, $F_i=[m_{iz} f_{ix} f_{iy}]^T$ （旋转分量和线性分量）。如果存在一个权重向量 $\in R^j ,k>=0$ ，使得对于所有 $F_ext \in R^n$ 有 $Fk + F_ext = 0$ , 那么接触将产生形封闭。
如图所示，平面物体中心有一个孔，两个手指分别与孔的两个不同边缘接触，产生四条接触法线
F=[F_1,F_2,F_3,F_4].
在这里插入图片描述
求解程序

import numpy as np
from scipy.optimize import linprog 
F1=[0,-1,0]
F2=[0,0,-1]
F3=[-1,1,0]
F4=[2,0,1]
F = np.array([F1,F2,F3,F4]).transpose()
# print(F)
f = [1,1,1,1]
A_eq= F 
b_eq=np.zeros(F.shape[0])
# print(b_eq)
A = [[-1,0,0,0],[0,-1,0,0],[0,0,-1,0],[0,0,0,-1]]
b=[-1,-1,-1,-1]
k=linprog(f,A,b,A_eq,b_eq)
k

输出如下

        message: Optimization terminated successfully. (HiGHS Status 7: Optimal)success: Truestatus: 0fun: 6.0x: [ 2.000e+00  1.000e+00  2.000e+00  1.000e+00]nit: 0lower:  residual: [ 2.000e+00  1.000e+00  2.000e+00  1.000e+00]marginals: [ 0.000e+00  0.000e+00  0.000e+00  0.000e+00]upper:  residual: [       inf        inf        inf        inf]marginals: [ 0.000e+00  0.000e+00  0.000e+00  0.000e+00]eqlin:  residual: [ 0.000e+00  0.000e+00  0.000e+00]marginals: [-2.000e+00 -1.000e+00  5.000e+00]ineqlin:  residual: [ 1.000e+00  0.000e+00  1.000e+00  0.000e+00]marginals: [-0.000e+00 -6.000e+00 -0.000e+00 -0.000e+00]mip_node_count: 0mip_dual_bound: 0.0mip_gap: 0.0

k的解是存在的，但如果把右侧手指移动到孔的右下角，那么F矩阵为

array([[ 0,  0,  0, -2],[-1,  0,  1,  0],[ 0, -1,  0, -1]])

但是无解，不能形封闭

from 现代机器人学，一阶形封闭

抓取方法简单计算流程

基于Force-closure评估的抓取计算流程示例
在这里插入图片描述

在这里插入图片描述

Robotic Manipulation-Planar Pushing

数据集：https://web.mit.edu/mcube/push-dataset/;
https://web.mit.edu/mcube/omnipush-dataset/index.html
多指抓取（Multi-finger Grasping) Dex -YCB
双指抓取：planar grasping(rectangle ; $x,y,w,h,\theta$ )
6Dof grasping(more general)

在这里插入图片描述

push

机器人实用案例

在这里插入图片描述

Ref

https://www.shenlanxueyuan.com/course/727/task/29297/show

现代机器人学-抓握与操作

• Unified impedance and admittance control
• Modern Control Engineering (Ogata)
• An overview of 3D object grasp synthesis algorithms
• Tutorial: Fundamentals of Robotic Manipulation and Grasping by Alberto Rodriguez, MIT
• Robotic Manipulation Perception, Planning, and Control by Russ Tedrake, MIT
• principles of robot autonomy II Stanford
• Springer Handbook of Robotics – Grasping
• A Mathematical Introduction to Robotic Manipulation
• More than a Million Ways to Be Pushed: A High-Fidelity Experimental Dataset of Planar Pushing