算法day_3数组中的单一元素和二进制位颠倒

本文将介绍两道经典的位运算题目，这些题目经常出现在各大公司的技术面试中。通过这些题目，我们可以更好地理解位运算的应用。

题目一

数组中只出现一次的数（其它数出现 $k$ 次）

来源：LeetCode 137. Single Number II 的变种题
牛客网 NC156 数组中只出现一次的数（其它数出现 $k$ 次）

描述

给定一个长度为 $n$ 的整型数组 arr 和一个整数 $k$ ( $k > 1$ )。

已知 arr 中只有 1 个数出现一次，其他的数都出现 $k$ 次。

请返回只出现了 1 次的数。

数据范围:

$\leq n \leq 2 \times 10^5$
$1 < k < 100$
$\times 10^9 \leq arr[i] \leq 2 \times 10^9$

📝 进阶：时间复杂度 $O (n)$ ，空间复杂度 $O (1)$

示例 1

输入：

[5,4,1,1,5,1,5],3

返回值：

示例 2

输入：

[2,2,1],2

返回值：

难度：中等

解题思路

方法一：哈希表法

利用哈希表统计每个元素出现的次数，空间换时间的典型解法。

思路

使用 unordered_map 统计数组中每个元素出现的次数。
遍历哈希表，找到出现次数为 1 的元素。

代码实现

// 时间复杂度：O(n)
// 空间复杂度：O(n)
int foundOnceNumber(vector<int>& arr, int k) {unordered_map<int, int> frequency;for (int num : arr) {frequency[num]++;}for (const auto& [num, count] : frequency) {if (count == 1) {return num;}}return -1; // 若未找到，返回 -1
}

方法二：位运算法（推荐）

位运算的巧妙应用，空间复杂度降为 $O (1)$ 。

核心思想

对整数的每一位分别统计。
对于每一位，统计所有数字在该位上 1 的出现次数之和。
如果某一位上 1 的总数不是 $k$ 的倍数，说明只出现一次的数字在该位上为 1。

详细步骤

初始化结果变量 result = 0。
对于每一位 i（从 0 到 31）：
- 统计数组中所有数字在第 i 位上 1 的总个数 sum。
- 如果 sum % k != 0，将结果 result 的第 i 位置为 1。
返回结果 result。

代码实现

// 时间复杂度：O(n)
// 空间复杂度：O(1)
int foundOnceNumber(vector<int>& arr, int k) {int result = 0;for (int i = 0; i < 32; i++) {int sum = 0;for (int num : arr) {sum += (num >> i) & 1; // 获取 num 在第 i 位的值}if (sum % k != 0) {result |= (1 << i); // 将第 i 位置为 1}}return result;
}

注意事项

处理负数：由于负数在计算机中以补码形式存储，右移时需要注意符号扩展，可以使用无符号数来避免问题。
优化：若数组中存在负数，需将 num 转换为 unsigned int 进行位运算。

改进代码

int foundOnceNumber(vector<int>& arr, int k) {int result = 0;for (int i = 0; i < 32; i++) {int sum = 0;for (int num : arr) {unsigned int temp = num;sum += (temp >> i) & 1;}if (sum % k != 0) {result |= (1 << i);}}return result;
}

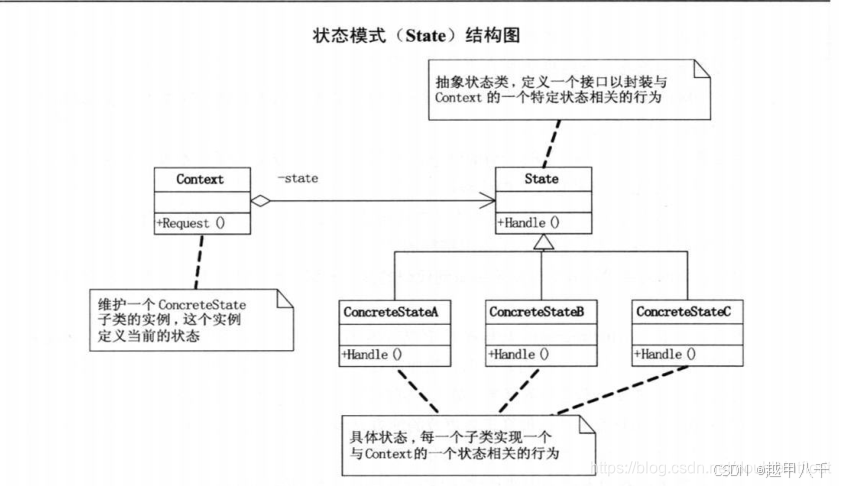
方法三：状态机法（特殊情况下适用）

当 $k = 3$ 时，可使用状态机法进一步优化。

代码示例

int singleNumber(vector<int>& nums) {int ones = 0, twos = 0;for (int num : nums) {ones = (ones ^ num) & ~twos;twos = (twos ^ num) & ~ones;}return ones;
}

说明

该方法利用二进制位的状态转换，适用于某些特定的 $k$ 值。

题目二

190. 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

提示

在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，但不影响实际的二进制位操作。

示例 1

输入：

n = 00000010100101000001111010011100

输出：

964176192 (00111001011110000010100101000000)

解释：

输入的二进制串表示无符号整数 43261596。
返回的二进制串表示无符号整数 964176192。

示例 2

输入：

n = 11111111111111111111111111111101

输出：

3221225471 (10111111111111111111111111111111)

解释：

输入的二进制串表示无符号整数 4294967293。
返回的二进制串表示无符号整数 3221225471。

难度：简单

解题思路

我们需要将给定的 32 位无符号整数的二进制位按位翻转。

方法一：逐位翻转

思路

初始化结果变量 result = 0。
遍历给定整数的每一位（共 32 位）：
1. 将 result 左移一位，为下一位腾出位置。
2. 取出 n 的最低位 (n & 1)，加入到 result 中。
3. 将 n 右移一位，准备处理下一位。
返回结果 result。

代码实现

uint32_t reverseBits(uint32_t n) {uint32_t result = 0;for(int i = 0; i < 32; i++){result <<= 1;        // 左移一位result |= (n & 1);   // 加入最低位n >>= 1;             // 右移一位}return result;
}

方法二：位操作优化（分治法）

思路

使用位操作技巧，分组交换二进制位，达到翻转的目的。
具体步骤：
1. 将高 16 位与低 16 位交换。
2. 将每个 16 位中的高 8 位与低 8 位交换。
3. 将每个 8 位中的高 4 位与低 4 位交换。
4. 将每个 4 位中的高 2 位与低 2 位交换。
5. 将每个 2 位中的高 1 位与低 1 位交换。

代码实现

uint32_t reverseBits(uint32_t n) {n = (n >> 16) | (n << 16); // 交换高低 16 位n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8); // 交换每个 16 位内的高低 8 位n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4); // 交换每个 8 位内的高低 4 位n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2); // 交换每个 4 位内的高低 2 位n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1); // 交换每个 2 位内的高低 1 位return n;
}

解释

使用掩码和移位操作，实现不同位数的高低位交换，从而达到整体翻转的效果。

方法三：查表法（缓存法）

思路

将 32 位分成 4 个字节（8 位），预先计算 256（ $2^8$ ）个可能的字节翻转结果，存入数组。
遍历每个字节，利用查表快速获取翻转结果。

代码实现

static uint8_t reverseByte(uint8_t byte) {byte = (byte >> 4) | (byte << 4);byte = ((byte & 0xCC) >> 2) | ((byte & 0x33) << 2);byte = ((byte & 0xAA) >> 1) | ((byte & 0x55) << 1);return byte;
}uint32_t reverseBits(uint32_t n) {static unordered_map<uint8_t, uint8_t> cache;uint32_t result = 0;for (int i = 0; i < 4; ++i) {uint8_t byte = (n >> (i * 8)) & 0xFF;if (cache.find(byte) == cache.end()) {cache[byte] = reverseByte(byte);}result |= (uint32_t)(cache[byte]) << ((3 - i) * 8);}return result;
}