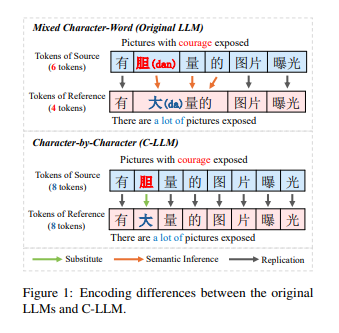
机器学习及KNN算法
目录
- 机器学习及KNN算法
- 机器学习基本概念
- 概念理解
- 步骤
- 为什么要学习机器学习
- 需要准备的库
- KNN算法
- 概念
- 算法导入
- 常用距离公式
- 算法优缺点
- 优点:
- 缺点︰
- 数据可视化
- 二维界面
- 三维界面
- KNeighborsClassifier 和KNeighborsRegressor理解
- 查看KNeighborsRegressor函数参数定义
- 查看 KNeighborsClassifier函数参数定义
- 参数理解
- 使用格式
- 预测类别实际应用
- 问题
- 特征数据
- 类别标签
- 问题理解
- 可视化数据理解
- 数据预测
- 预测数值实际应用
机器学习基本概念
概念理解
利用数学中的公式 总结出数据中的规律。
步骤
- 数据收集
数据量越大,最终训练的结果越正确 - 建立数学模型训练
针对不同的数据类型需要选择不同的数学模型 - 预测
预测数据
为什么要学习机器学习
- 信息爆炸时代,数据量太大,人工已经无法处理。
- 重复性的工作交给电脑来做。
- 潜在一些信息之间的关联人类不容易直接发现。
- 机器学习确实有效的解决很多问题。
等…
需要准备的库
- numpy
- scipy
- matplotlib
- pandas
- sklearn
Sklearn (Scikit-Learn) 是基于 Python 语言的第三方机器学习库。它建立在 NumPy, SciPy, Pandas 和 Matplotlib库 之上,里面的 API 的设计非常好,所有对象的接口简单,很适合新手上路。我使用的是1.0.2版本,可在终端下载
代码展示:
未修改pip下载源的,后面需添加 -i 镜像源地址
pip install scikit_learn==1.0.2
KNN算法
概念
全称是k-nearest neighbors,通过寻找k个距离最近的数据,来确定当前数据值的大小或类别。是机器学习中最为简单和经典的一个算法。
如果求得是值,则求其平均值为结果,如果是确定类别,则比较多的类别为结果。
算法导入
- KNeighborsClassifier 预测类别
- KNeighborsRegressor 预测值
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
常用距离公式
-
欧式距离:
- 二维空间:a点为(x1,y1),b点为(x2,y2)

- 三维空间:a点为(x1,y1 ,z1),b点为(x2,y2 ,z2)

- n维空间:a点为(x11,x12 ,…,x1n),b点为(x21,x22,…,x2n)

- 二维空间:a点为(x1,y1),b点为(x2,y2)
-
曼哈顿距离:
-
二维空间:a点为(x1,y1),b点为(x2,y2)

-
n维空间:a点为(x11,x12 ,…,x1n),b点为(x21,x22,…,x2n)

-
算法优缺点
优点:
1.简单,易于理解,易于实现,无需训练;
2.适合对稀有事件进行分类;
3.对异常值不敏感。
缺点︰
1.样本容量比较大时,计算时间很长;
⒉.不均衡样本效果较差;
数据可视化
二维界面
格式:
- figure(“窗口名”)
创建空白画板 - axes()
确认维度,默认二维 - scatter(x,y,c=“十六进制颜色值”,marker=“标识图案”)
设置为散点图,同时确认数据及数据显示颜色和标识图案,x,y可以是数值也可以是数组 - set(xlabel=“x”,ylabel=“y”)
设置坐标轴名称,x,y可以改为需要的坐标轴名
代码展示:
import matplotlib.pyplot as plt
a = [1,2,3,4]
# 建立空白画板
fig = plt.figure("二维")
#确认维度,默认二维
b = plt.axes()
# 数据可以是数值也可以是数组
b.scatter(2,3,c="#00F5FF",marker="o")
b.scatter(a,a,c="#00FF7F",marker="*")
b.set(xlabel="x",ylabel="y")
plt.show()
运行结果:

三维界面
格式:
- figure(“窗口名”)
创建空白画板- axes(projection=“3d”)
设置三维 - scatter(x,y,z,c=“十六进制颜色值”,marker=“标识图案”)
确认数据及数据显示颜色和标识图案,x,y,z可以是数值也可以是数组
- axes(projection=“3d”)
- set(xlabel=“x”,ylabel=“y”,zlabel=“z”)
设置坐标轴名称,x,y,z可以改为需要的坐标轴名
代码展示:
a = [1,2,3,4]
data = np.loadtxt('dating_TS.txt')
figure = plt.figure("三维")
b = plt.axes(projection="3d")
b.scatter(2,3,4,c="#00F5FF",marker="o")
b.scatter(a,a,a,c="#00FF7F",marker="*")
b.set(xlabel="x",ylabel="y",zlabel="z")
plt.show()
运行结果:

KNeighborsClassifier 和KNeighborsRegressor理解
查看KNeighborsRegressor函数参数定义
按住CTRL,鼠标点击函数可自动跳转
部分代码展示:
def __init__(self,n_neighbors=5,*,weights="uniform",algorithm="auto",leaf_size=30,p=2,metric="minkowski",metric_params=None,n_jobs=None,)
查看 KNeighborsClassifier函数参数定义
部分代码展示:
def __init__(self,n_neighbors=5,*,weights="uniform",algorithm="auto",leaf_size=30,p=2,metric="minkowski",metric_params=None,n_jobs=None,)
参数理解
- n_neighbors
k值,邻居的个数,默认为5。【关键参数】 - weights : 权重项,默认uniform方法。
- Uniform:所有最近邻样本的权重都一样。【一般使用这一个】
- Distance:权重和距离呈反比,距离越近的样本具有更高的权重。【确认样本分布情况,混乱使用这种形式】
- Callable:用户自定义权重。
- algorithm :用于计算最近邻的算法。
- ball_tree:球树实现
- kd_tree:KD树实现, 是一种对n维空间中的实例点进行存储以便对其进行快速搜索的二叉树结构。
- brute:暴力实现
- auto:自动选择,权衡上述三种算法。【一般按自动即可】
leaf_size :空值KD树或者球树的参数,停止建子树的叶子节点的阈值。
- p : 距离的计算方式。P=1为曼哈顿距离,p=2为欧式距离。
1.曼哈顿距离2.欧式距离3.切比雪夫距离4.闵可夫斯基距离5.带权重闵可夫斯基距离
6.标准化欧式距离7.马氏距离 - metric : 用于树的距离度量
“euclidean” EuclideanDistance -sqrt(sum((x - y)^2))
“manhattan” ManhattanDistance -sum(|x - y|)
“chebyshev” ChebyshevDistance -max(|x - y|)
“minkowski” MinkowskiDistance p, wsum(w * |x - y|^p)^(1/p)
“wminkowski” WMinkowskiDistance p, wsum(|w * (x - y)|^p)^(1/p)
“seuclidean” SEuclideanDistance Vsqrt(sum((x - y)^2 / V))
“mahalanobis” MahalanobisDistance V or VI ``sqrt((x - y)’ V^-1 (x - y)) - metric_params :用于比较复杂的距离的度量附加参数。【用不上】
使用格式
- x = data1 特征数据
- y = data2 结果(平均值/较多类别)
- n = KNeighborsClassifier(n_neighbors=7,p=1,metric=“euclidean”)
确定最近个数为7,和距离计算方式1曼哈顿距离,树的距离方式是欧式距离 - n.fit(x,y)
自带的训练模型,自动按上方设置计算判断 - n.predict(二维数组)
预测二维数组的结果
预测类别实际应用
问题
现在有很多大学里出现室友矛盾,假如室友可以选择: 大学里面 ,对于校方,把类型相同的学生放在一个寝室,在基于大二大三大四的,现已存在一个数据文件datingTestSet2.txt ,为历年大学生的调查问卷表。
特征数据
第1列:每年旅行的路程
第2列:玩游戏所有时间百分比
第3列:每个礼拜消 零食
类别标签
1表示爱学习,2表示一般般,3表示爱玩,目的为学生在大学中挑选室友的信息
datingTestSet2.txt 部分数据展示:

问题理解
根据最近距离的k个距离最近的类别标签来预测要确定如有[1500,0.924729,0.2134935]特征数据的学生的类别标签,进而分寝室。
注意点:最近距离是由三列特征数据来计算,结果是类别,需要使用的是KNeighborsClassifier
可视化数据理解
data[:,-1] 索引数据最后一列
data[:,-1] ==1 判断为类别1为T,否则为F,结果是bool值
data[data[:,-1]==1] 根据判断归类各个类别数据
data_1[:,0],data_1[:,1],data_1[:,2] 分别为第1,2,3列特征数据
由颜色表示类别3种
调试查看数据data

data[:,-1]

data[:,-1] ==1

data[data[:,-1]==1]

代码展示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
data = np.loadtxt('dating_TS.txt')
data_1 = data[data[:,-1]==1]
data_2 = data[data[:,-1]==2]
data_3 = data[data[:,-1]==3]
a_d = data[:,-1]
a_d_1 = [data[:,-1]==1]
fig = plt.figure()
a = plt.axes(projection="3d")
a.scatter(data_1[:,0],data_1[:,1],data_1[:,2],c="#00F5FF",marker="o")
a.scatter(data_2[:,0],data_2[:,1],data_2[:,2],c="#00FF7F",marker="o")
a.scatter(data_3[:,0],data_3[:,1],data_3[:,2],c="#000080",marker="o")
a.set(xlabel="x",ylabel="y",zlabel="z")
plt.show()
运行结果:

数据预测
代码展示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
data = np.loadtxt('dating_TS.txt')
x = data[: , :-1]
y = data[: , -1]
n = KNeighborsClassifier(n_neighbors=7,p=1)
n.fit(x,y)
print(n.predict([[1500,0.924729,0.2134935]]))
p_data = [[1234,2.4567,0.5467],[123435,8.2134,2.345],[5668,3.6754,0.34567]
]
print(n.predict(p_data))
n1 = KNeighborsClassifier(n_neighbors=3,p=2,metric="euclidean")
n1.fit(x,y)
print(n1.predict([[1500,0.924729,0.2134935]]))
p_data = [[1234,2.4567,0.5467],[123435,8.2134,2.345],[5668,3.6754,0.34567]
]
print(n1.predict(p_data))
运行结果:

预测数值实际应用
给定房屋特征和价格数据,最后一列为价格,来根据历史数据预测价格
部分房屋特征和价格数据展示:

代码展示:
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
data_f = np.loadtxt('data_f1.txt')
x = data_f[:,:-1]
y = data_f[:,-1]
n = KNeighborsRegressor(n_neighbors=7,p=2,metric="euclidean")
n.fit(x,y)
print(n.predict([[ 2.82838,0.00,18.120,0,0.5320,5.7620,40.32,4.0983,24,666.0,20.21,392.93,10.42]]))
n1 = KNeighborsRegressor(n_neighbors=5,p=2,metric="euclidean")
n1.fit(x,y)
print(n1.predict([[ 2.82838,0.00,18.120,0,0.5320,5.7620,40.32,4.0983,24, 666.0,20.21,392.93,10.42]]))
运行结果:






![JS面试题|[2024-12-26]](https://i-blog.csdnimg.cn/direct/be320fbc28cb44e39e6db9ea2f16e3dc.jpeg)