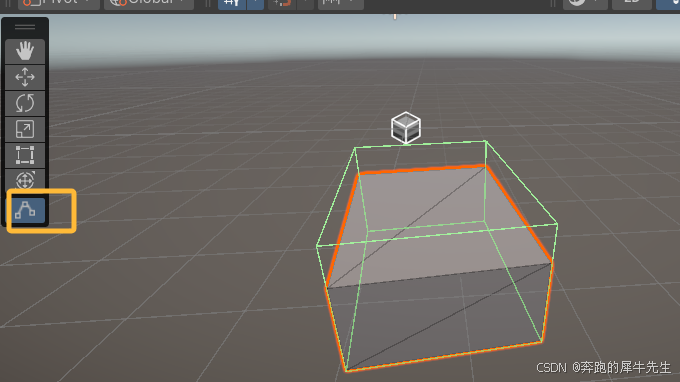
特征向量与特征值编程实现
文章目录
- 特征向量与特征值编程实现
- 1、什么是特征向量
- 2、特征向量背后的直觉
- 3、为什么特征向量很重要?
- 4、如何计算特征向量?
- 4、特征向量Python实现
- 5、可视化特征向量
- 6、总结
线性代数是许多高级数学概念的基石,广泛应用于数据科学、机器学习、计算机视觉和工程领域。线性代数的基本概念之一是特征向量,通常与特征值配对。但特征向量到底是什么?为什么它如此重要?
本文以简单直观的方式分解了特征向量的概念,让任何人都能轻松掌握。
1、什么是特征向量
方阵与一种称为特征向量的特殊向量相关联。当矩阵作用于特征向量时,它会保持特征向量的方向不变,并且仅通过称为特征值的标量值对其进行缩放。
从数学角度来说,对于方阵 A,如果满足以下条件,则非零向量 v 是特征向量:

其中:
- A 是矩阵。
- v 是特征向量。
- λ 是特征值(标量)。
2、特征向量背后的直觉
假设您有一个矩阵 A,它表示线性变换,例如拉伸、旋转或缩放 2D 空间。当将此变换应用于向量 v 时:
大多数向量会改变其方向和大小。
但是ÿ