1. 古典概型、几何概型
- 古典概型——有限等可能(有限个可能事件,且每个事件都是等可能概率事件)
- 几何概型——无限等可能
2. 条件概率
若 P ( B ) > 0 P(B)>0 P(B)>0,称在 B B B 发生的条件下, A A A 发生的概率为条件概率,且 P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB).
3. 全概率公式
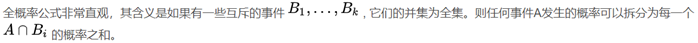
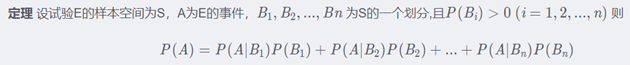
若 B 1 , B 2 , … B n B_1,B_2,… B_n B1,B2,…Bn 为 Ω Ω Ω 的一个完备事件组,则对任一事件 A A A ,有 P ( A ) = ∑ ( i = 1 ) n P ( B i ) P ( A ∣ B i ) P(A)=∑_{(i=1)}^n P(B_i )P(A|B_i) P(A)=∑(i=1)nP(Bi)P(A∣Bi).
4. 贝叶斯公式
贝叶斯本质就一个条件概率公式 P ( A ∣ B ) P(A|B) P(A∣B),也就是在 B B B 事件发生的情况下, A A A 事件发生的概率。

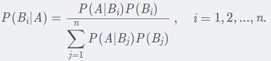
5. 什么是先验概率?
事情未发生,只根据以往数据统计,分析事情发生的可能性,即先验概率。
指根据以往经验和分析。在实验或采样前就可以得到的概率。
先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现。
6. 什么是后验概率?与先验概率的关系?
1) 后验概率
事情已发生,已有结果,求引起这事发生的因素的可能性,由果求因,即后验概率。
指某件事已经发生,想要计算这件事发生的原因是由某个因素引起的概率。
后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,如贝叶斯公式中的,是"执果寻因"问题中的"因"。
2) 与先验概率的关系
后验概率的计算,是以先验概率为前提条件的。如果只知道事情结果,而不知道先验概率(没有以往数据统计),是无法计算后验概率的。
后验概率的计算需要应用到贝叶斯公式。
7. 全概率公式、贝叶斯公式与先验、后验概率的关系?
全概率公式,总结几种因素,事情发生的概率的并集。由因求果。
贝叶斯公式,事情已经发生,计算引起结果的各因素的概率,由果寻因。同后验概率。
全概率是用原因推结果,贝叶斯是用结果推原因。
8. 离散型随机变量的常见分布

1) 伯努利分布\两点分布\0-1分布 X ∼ B ( 1 , p ) X∼B(1,p) X∼B(1,p)
P ( X = 0 ) = 1 − p , P ( X = 1 ) = p , p ∈ ( 0 , 1 ) P(X=0)=1-p, P(X=1)=p, p∈(0,1) P(X=0)=1−p,P(X=1)=p,p∈(0,1)
2) 二项分布(伯努利概型) X ∼ B ( n , p ) X∼B(n,p) X∼B(n,p)
P ( X = k ) = C n k p k ( 1 − p ) n − k , p ∈ ( 0 , 1 ) , k = 0 , 1 , … , n P(X=k)=C_n^k p^k (1-p)^{n-k}, p∈(0,1), k=0,1,…,n P(X=k)=Cnkpk(1−p)n−k,p∈(0,1),k=0,1,…,n
N N N 次独立重复的伯努利试验中成功的次数 X X X 服从二项分布。
3) 泊松分布 X ∼ P ( λ ) X∼P(λ) X∼P(λ)
P ( X = k ) = λ k e − λ k ! , λ > 0 , k = 0 , 1 , 2 , … P(X=k)=\frac{λ^k e^{-λ}}{k!}, λ>0, k=0,1,2,… P(X=k)=k!λke−λ,λ>0,k=0,1,2,…
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。
4) 几何分布 X ∼ G ( p ) X∼G(p) X∼G(p)
P ( X = k ) = ( 1 − p ) ( k − 1 ) p , p ∈ ( 0 , 1 ) , k = 1 , 2 , … P(X=k)=(1-p)^{(k-1)} p, p∈(0,1), k=1,2,… P(X=k)=(1−p)(k−1)p,p∈(0,1),k=1,2,…
首次试验成功所需做的试验次数 X X X 服从几何分布。
5) 超几何分布
超几何分布(Hypergeometric distribution)描述了由有限个对象中抽出 n n n 个对象,成功抽出 k k k 次指定种类的对象的概率(抽出不放回(without replacement))。
P ( X = k ) = C K k C N − K n − k C N n , 0 < k < m i n { K , n } P(X=k)=\frac{C_K^k C_{N-K}^{n-k}}{C_N^n },0<k<min\{K,n\} P(X=k)=CNnCKkCN−Kn−k,0<k<min{K,n}

9. 连续型随机变量的常见分布

1) 均匀分布 X ∼ U ( a , b ) X∼U(a,b) X∼U(a,b)
f ( x ) = { 1 b − a a < x < b 0 o t h e r f(x)=\begin{cases}\frac{1}{b-a}&a<x<b\\0&other\end{cases} f(x)={b−a10a<x<bother
2) 指数分布 X ∼ E ( λ ) X∼E(λ) X∼E(λ)
f ( x ) = { λ e − λ x x > 0 0 o t h e r f(x)=\begin{cases}λe^{-λx}&x>0\\0&other\end{cases} f(x)={λe−λx0x>0other
3) 正态分布\高斯分布 X ∼ N ( μ , σ 2 ) X∼N(μ,σ^2) X∼N(μ,σ2)
f ( x ) = 1 √ 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ < x < ∞ f(x)=\frac{1}{√2π σ} e^{-\frac{(x-μ)^2}{2σ^2}}, -∞<x<∞ f(x)=√2πσ1e−2σ2(x−μ)2,−∞<x<∞
特别地,当 μ = 0 , σ = 1 μ=0, σ=1 μ=0,σ=1 时为标准正态分布, X ∼ N ( 0 , 1 ) X∼N(0,1) X∼N(0,1) .

10. 若干正态分布相加、相乘后得到的分布分别是什么?
(独立的前提下)都服从正态分布。

11. 数学期望、方差
1) 数学期望
随机变量的均值(不同于样本均值),大数定律指出如果样本足够的话,样本均值会无限接近数学期望。
数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
2) 方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
方差是衡量源数据和期望值相差的度量值。
D ( X ) = E ( ( X − E ( X ) ) 2 ) = E ( X 2 ) − E 2 ( X ) D(X)=E((X-E(X))^2)=E(X^2)-E^2(X) D(X)=E((X−E(X))2)=E(X2)−E2(X) (平方的期望-期望的平方)
12. 相关系数、协方差
1) 协方差
期望值分别为 E [ X ] E[X] E[X] 与 E [ Y ] E[Y] E[Y] 的两个实随机变量 X X X 与 Y Y Y 之间的协方差 C o v ( X , Y ) Cov(X,Y) Cov(X,Y) 定义为:
即: X , Y X, Y X,Y 的协方差等于每一个 X X X 减去 X X X 平均值乘上每一个 Y Y Y 减去 Y Y Y 平均值的乘积的和的平均数。
从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
从直观上来看,协方差表示的是两个变量总体误差的期望。
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
2) 相关系数
定义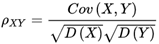 称为随机变量 X X X 和 Y Y Y 的(Pearson)相关系数。
称为随机变量 X X X 和 Y Y Y 的(Pearson)相关系数。
即:用 X 、 Y X、Y X、Y 的协方差除以 X X X 的标准差和 Y Y Y 的标准差。
相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
3) 相关系数或协方差为0的时候能否说明两个分布无关?为什么?
只能说明不线性相关,不能说明无关。因为在数学期望存在的情况下,独立必不相关,不相关未必独立。
13. 独立和互斥的关系?

14. 独立和不相关的区别?
不相关就是两者没有线性关系,但是不排除其它关系存在;独立就是互不相干没有关联。
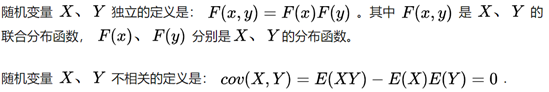 (cov 协方差)
(cov 协方差)
在数学期望存在的情况下,独立必不相关,不相关未必独立。
15. 大数定律
随机变量的均值依概率收敛于自己的期望。
大数定律通俗一点来讲,就是样本数量很大的时候,样本均值和数学期望充分接近,也就是说当我们大量重复某一相同的实验的时候,其最后的实验结果可能会稳定在某一数值附近。就像抛硬币一样,当我们不断地抛,抛个上千次,甚至上万次,我们会发现,正面或者反面向上的次数都会接近一半,也就是这上万次的样本均值会越来越接近 50 % 50\% 50% 这个真实均值,随机事件的频率近似于它的概率。

实验次数越多,样本均值趋向于总体的均值。大数定理将属于数理统计的平均值和属于概率论的期望联系在了一起。

16. 切比雪夫大数定律
设 X 1 , X 2 , … , X n X_1,X_2,…,X_n X1,X2,…,Xn 独立,期望 E X k EX_k EXk,方差 D X k DX_k DXk 都存在,且方差 D X k DX_k DXk 有一致上界(即每个方差都有上界且收敛速度接近),则对任意 ε > 0 ε >0 ε>0,有: 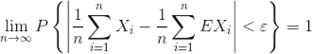 . (不要求同分布)
. (不要求同分布)
17. 中心极限定理
大量( n → ∞ n→∞ n→∞)、独立、同分布的随机变量之和,近似服从于一维正态分布。
n n n 个独立同分布的随机变量,当 n n n 充分大时,其均值服从正态分布。(大量独立同分布的随机变量之和近似服从一维正态分布。)
中心极限定理是说当样本数量无穷大的时候,样本均值的分布呈现正态分布。
实验次数越多,样本均值的分布越趋向于正态分布。
中心极限定理指的是给定一个任意分布的总体。每次从这些总体中随机抽取 n n n 个抽样,一共抽 m m m 次。 然后把这 m m m 组抽样分别求出平均值。这些平均值的分布接近正态分布。
18. 大数定律和中心极限定理的区别
前者更关注的是样本均值,后者关注的是样本均值的分布,比如说掷色子吧,假设一轮掷色子 n n n 次,重复了 m m m 轮,当 n n n 足够大,大数定律指出这 n n n 次的均值等于随机变量的数学期望,而中心极限定理指出这 m m m 轮的均值分布符合围绕数学期望的正态分布。
19. 最大似然估计(极大似然估计)是什么?
极大似然估计就是一种参数估计方法。
最大似然估计的目的是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
方程的解只是一个估计值,只有在样本数趋于无限多的时候,它才会接近于真实值。
-
求最大似然估计量 θ ^ \widehat \theta θ 的一般步骤:
[1] 写出似然函数;
[2] 对似然函数取对数,并整理;
[3] 求导数;
[4] 解似然方程。 -
最大似然估计的特点:
[1] 比其他估计方法更加简单;
[2] 收敛性:无偏或者渐近无偏,当样本数目增加时,收敛性质会更好;
[3] 如果假设的类条件概率模型正确,则通常能获得较好的结果。但如果假设模型出现偏差,将导致非常差的估计结果。