《三体》电视剧的播出，还原了很多原著小说中的“名场面”，引发了公众和书迷的广泛关注和讨论。对于等不及电视剧更新去翻书的人，亦或是“原著党”的脑海里，“名场面”一定少不了《三体3：死神永生》中，“歌者”投出“二向箔”让整个太阳系受到降维打击变成二维化的这一幕。

实际上在小说《三体3：死神永生》中，主角程心和“万有引力”号随舰学者关一帆也讨论过星际战争中可能使用的最有威力的武器：

“……还有其他的宇宙规律被用作武器，但目前为止我们还不知道都有哪些，很可能，所有的规律都能被武器化了，在宇宙的某一部分，被用作武器的规律甚至可能包括……当然这只是瞎猜，太玄乎，我也不相信。”

“包括什么？”

“数学规律。”

或许宇宙规律是最可怕的武器——在《三体》小说中，最常被利用的两种宇宙规律分别是空间维度和光速，前者的代表就是大家熟知的“二向箔”，后者则是所谓的低光速黑洞。

“二向箔”的关键词是维数，这也是数学中最重要的基础概念之一。那么从数学规律而言，“二向箔”真的存在吗？

答案是：

在现有的数学规律下，并不可能。

下面就告诉你为什么“不可能”。

数学中的“维数”概念

下面的图像从左到右分别代表了从零维到三维的物体：点、线段、平面、实心立方体，与我们平常生活的经验相符。

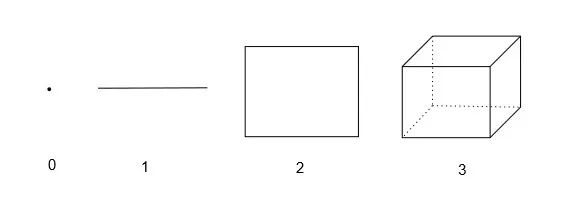
更为抽象的四维及以上的空间可以通过类比法帮助大家理解。例如，一个生活在平面上的二维生物，怎样通过盲人摸象的手段来想象三维空间中的一个实心球？

我们不妨用x，y，t三个字母来分别表示三维空间中的三个坐标，那么三维空间中的实心球由如下的不等式定义：x²+y²+t²≤1。其几何图像如下图红色部分所示，其中的红色射线代表x轴，蓝色射线代表y轴，绿色射线则代表t轴。

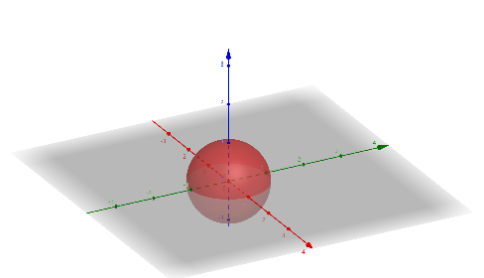
想象有一个生活在xy平面上的二维生物，其中字母t则代表了这个平面所处的时间。不同的时刻，t这个二维生物眼中看到的红色实体球会长什么样呢？

在左下图中，我们用浅绿色平面标出了t=-3，t=0，以及t=1这三个时刻xy平面的位置的斜视图，而下右图则是下左图的一个侧视图。

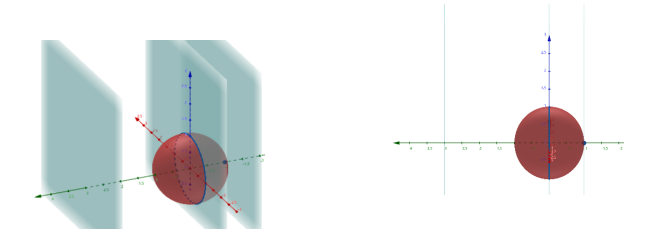
利用上面的两张图，我们不难发现在t=-3时刻，这个二维生物是看不到红球的。而在t=0时刻，红球在该生物眼中将是一个直径为1的实心圆盘。最后在t=1时刻该生物的眼中的红球则变为一个点。类似这样，我们让上面的浅绿色的平面随着时间t动起来，那么生活在这个浅绿色平面上的二维生物眼中看到的红色球将如下变化：

1)整个红色球都只出现在从-1到1的时刻之间；

2)在t=-1时刻，红色球是一个点。然后随时间的增大，这个点变为一个直径越来越大的实心圆盘，且在t=0的时刻其大小达到最大；

3)在t=0时刻后，该实心圆盘的直径随时间增加不断减小，直到t=1的时刻变为一个点，最后在t＞1的时刻完全消失掉。

下面的七张图显示了xy平面上的二维生物在不同时刻看到的红色实心球的大小的变化过程。

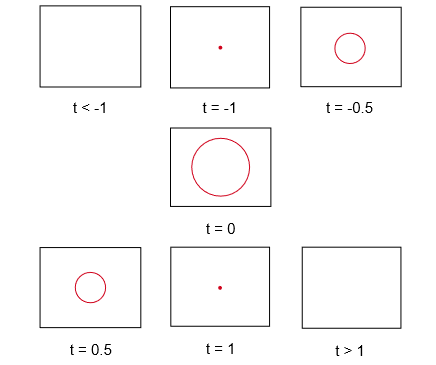
某二维生物眼中的三维实心球随时间的变化

基于上述举例，我们可以类比地想象四维空间中的实体球长什么样了。如果用x，y，z和t分别表示四维空间中的四个坐标，那么四维空间中的实心球的也可以用下面的不等式来定义：x²+y²+z²+t²≤1。

同样的，我们也可以假设其中的x，y，z就是我们所生活的三维空间的坐标，而t则代表了时间。那么，如果有一个人可以在时间的长河中自由来往穿梭，TA眼中的四维实心球就可以通过下面的方式来描述。这个四维的球将完全包含在-1≤t≤1的时刻中，并且在t=-1时是一个点，然后随时间t增大这个点将变为直径越来越大的三维实心球并在t=0时刻达到最大之后开始收缩，最终于t=1时刻坍缩为一个点并随即消失。

不妨想想，如果我们某天遇到了《三体》小说中所描述的四维碎片，那么它在我们眼中究竟长什么样？又或者某一天二维化宇宙中的某一个生物遇到了一个三维碎片，它眼中的三维碎片世界又是什么样的呢？

三维向二维之旅

根据《三体》小说中的描述，“二向箔”的作用是使得三维空间的其中一个维数坍缩后变成一个二维的空间。“二向箔”如何能做到这种坍缩？

我们还是以三维空间中的实心球来举例，将其类比为地球。最简单的方式当然就是投影法，就是日常我们见到阳光下物体的影子。下面左图就是将三维空间中的一个实心球体（红色）通过投影（灰色）变到二维平面（绿色）上的示意图，这个投影的像实际上是平面中的一个实心的圆盘。

但是，“二向箔”是通过投影来进行二维化的吗？《三体》小说原文的表述是二维化后的物体“都被精确地画下来”，显然投影是不符合的，因为上面右图中两个球的二维化图像跟左图中一个球的二维化图像是一样的，所以投影并不能精确地在二维平面上画出三维空间中的物体。

也就是说，如果我们要求精确地画出三维空间中的物体，那么首先我们必须保证三维空间中不同的点在二维平面中也将对应不同的点。 

那么，能否将三维空间中的实心球上的点放到一个二维平面中，使得球上任意不同的两点仍然是不同的呢？

答案是肯定的。

著名数学家康托（Georg Cantor）在1877年证明了任意维数的实心球体中的点都和单位区间[0,1]中的点一样多，即它们之间存在一对一的映射。这说明我们甚至可以将三维空间中的实心球变成二维平面中的一个线段，还能保证球面上不同的点在该线段中仍然是不同的。

为了方便理解，我们降个维度——以二维向一维的方式举例，尝试把一个二维实心正方形中的点一对一地放置到一条线段上。

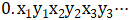首先不妨假设该实体正方形在二维平面中是由如下的不等式来定义：0≤x≤1和0≤y≤1。那么给定该正方形内部的一个点()，我们将把这个点放置到直线上的点处。比如正方形上的点(0.100···，0.222···)就将放在点0.120202···处。通过这种方式，我们刚好能够将正方形内部的点一对一地放置在开区间(0,1)点上。

然后我们可以把正方形的四条边截成两部分，分别粘在开区间(0,1)的两边，得到一个更大的开区间；最后再通过适当的放缩，就可以把实心正方形上的点一一放置于开区间(1,2)上的点，这一过程的几何示意图可以如下所示。

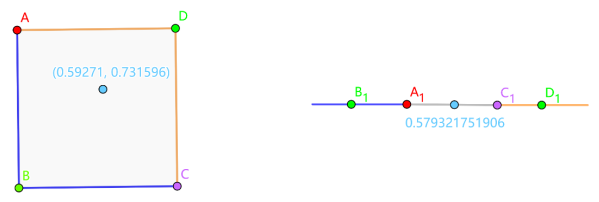
实心正方形与开区间的点一一对应

为了最终完成实心正方形与闭区间上的点的一一对应，我们现在只需要说明开区间(-1,2)与闭区间[-1,2]中的点是一一对应的。为此，让我们分别在开区间(-1,2)和闭区间[-1,2]中取如下的子集

开区间(-1,2)挖掉子集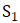后，与闭区间[-1,2]挖掉子集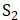后是一样的。因此，我们现在只需要将集合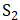中的点跟集合中的点一一对应起来就达到了最终目的。

从上面的书写方式中，可以发现如何实现这一过程：即只需要将两个集合中的点按照书写的先后次序一一对应起来即可。比如，可以将集合中点-1，2，0 和1 四个点分别对应于集合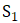中的点这四个点，最后将集合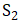中的其他形如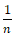等同于集合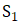中的点即可。通过这样的方式我们最终就实现了实心正方形[0,1]x[0,1]和闭区间[-1,2]上的点的一一对应。

闭区间与开区间上点的一一对应

上面这看似荒谬的结果其实极大地违反了我们的直觉，因为将实心正方形的内部变为开区间的过程完全打乱了正方形上的点之间的相对位置。比如原来在正方形上有两个点A和B，并且有一条连接A和B的线，那么我们就可以依次通过这条线上的点从A点走到B点。但将正方形变为线段时，这个线上的点的位置被完全打乱了，在线段上我们已经无法再按原来的点的次序连续地从A点走到B点了。

但《三体》小说中还提到，“二维化后的建筑结构变形很大，仅凭想象力从其二维图形推测出原来的三维形状几乎不可能，但毫无疑问，以正确的数学模型为基础的图像处理软件应该能够做到。”所以，从二维图像中恢复出三维的图像只使用点的个数是远远不够的，还必须知道不同的点之间的相对位置关系。

在数学中，如果两个空间中的点的数量一致，并且对应的点之间的相对位置也一致，那么我们就称这两个空间是同胚的。比如下面的两张图分别表明正六面体跟球面是同胚的，而轮胎则跟水杯是同胚的。

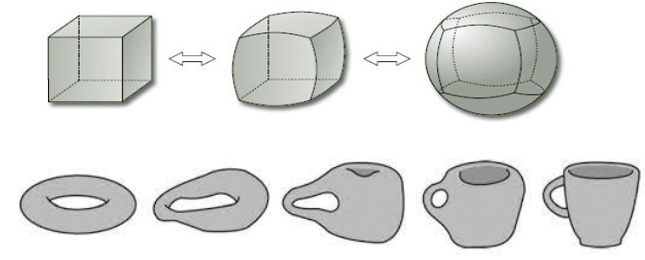
（图片来自网络）

也就是说，如果我们想要通过数学工具从三维物体的二维图像恢复出原来的三维物体，那么三维物体的二维图像必须要跟原来的三维物体同胚。

但这在数学上这是可能的吗？

答案是否定的。

在数学中我们称之为维数的不变性的定理，断言了两个同胚的空间必然有相同的维数。因此，我们不可能将三维的实心球同胚地做到二维化。

在历史上，前文所提到的康托的结果发表以后，数学家戴德金（Richard Dedekind）就在与康托的一封信件中提到维数的不变性问题。此后，很多数学家开始尝试给出这一结论的严格数学证明。但是，拓扑学作为数学中研究空间中点的位置关系的分支，在当时仍然非常“年轻”，很多重要的相关理论发展还不够充分，所以这一定理的严格证明直到1910年才由荷兰数学家布劳威尔（Luitzen Egbertus Jan Brouwer）完成。

至此，我们可以断言，在目前人类的数学世界中，是不可能二维化一个三维空间，同时还能保证不打乱这个空间中的点的相对位置关系。

当然，如果数学规律也像《三体》小说中所描述的“物理学不存在”了一样，其限制被完全打破，那么维数不变性定理对二向箔也就不再成立。至于怎样才能做到，大概只能等待歌者文明给我们解答了。

作者刘杰，系中国科学院数学与系统科学研究院基础数学科研人员

本账号稿件默认开启微信“快捷转载”

转载请注明出处

其他渠道转载请联系 weibo@cashq.ac.cn