集成学习：机器学习模型如何“博采众长”

前置概念

偏差

指模型的预测值与真实值之间的差异，它反映了模型的拟合能力。

方差

指模型在不同的训练集上产生的预测结果的差异，它反映了模型的稳定性。

在机器学习中，我们通常希望模型的偏差和方差都能够尽可能地小，从而达到更好的泛化能力。但是，偏差和方差的平衡是一个非常复杂的问题，很难通过简单的调参来解决。因此，在实际应用中，我们需要综合考虑模型的鲁棒性、准确性和泛化能力等多个指标，来评估模型的性能和可靠性。

拟合

模型过拟合指的是机器学习模型在训练集上表现很好，但在测试集或新数据上表现很差的情况。过拟合通常是由于模型过于复杂，或者训练数据过少、噪声过多等原因导致的。

欠拟合

模型欠拟合指的是机器学习模型在训练集和测试集上表现都不够好的情况。

决策树

决策树是一种基于树结构的分类算法，它通过构造一棵树来模拟决策过程。在决策树中，每个节点代表一个属性或特征，每个分支代表一个可能的取值，而每个叶子节点代表一个分类结果。决策树的工作原理是通过对数据集进行递归分割，将数据集划分为不同的子集，直到每个子集都属于同一类别或达到预定的停止条件。在分类时，将待分类样本从根节点开始，按照属性值依次向下遍历，直到到达叶子节点，即可得到分类结果。

鲁棒性

指模型对于输入数据中的噪声、异常值、缺失值等干扰因素的抵抗能力。在机器学习中，我们通常希望模型能够对于不同的输入数据都能够产生稳定和一致的输出结果，我们可以通过数据清洗、特征选择、模型调参等方法来提高模型的鲁棒性，从而提高模型的性能和准确性。

集成学习

核心思想是训练出多个模型并将这些模型进行组合。根据分类器的训练方式和组合预测的方法。目标就是，减少机器学习模型的方差和偏差，找到机器学习模型在欠拟合和过拟合之间的最佳平衡点。集成学习中两种最重要的方法就是：降低偏差的 Boosting 和降低方差的Bagging。

Boosting 方法

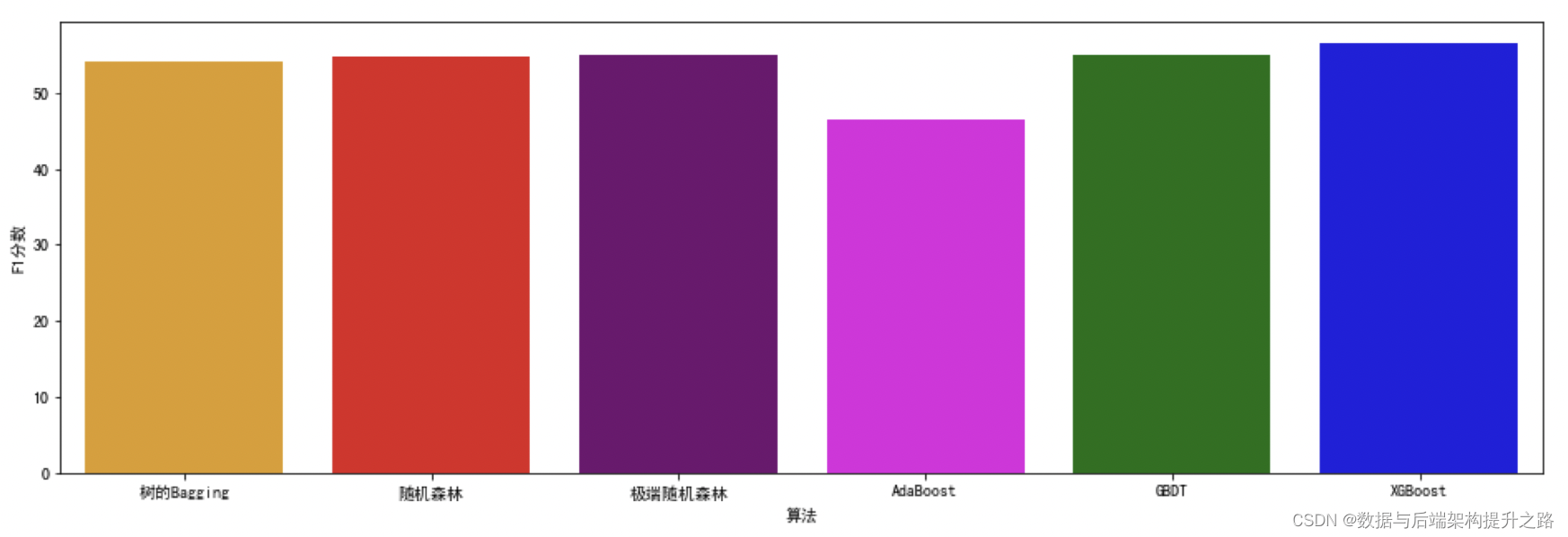
有三种很受欢迎的算法，分别是 AdaBoost、GBDT 和 XGBoost

AdaBoost

它通过持续优化一个基模型，将新模型整合到原有模型中，并对样本进行加权，以减小模型预测误差。

GBDT（梯度提升决策树）

将梯度下降和 Boosting 方法结合的算法。它采用决策树模型，并定义一个损失函数，通过梯度下降来优化模型。

XGBoost（极端梯度提升）

对 GBDT 进一步优化的算法。它也采用决策树模型，并定义一个损失函数。与 GBDT 不同的是，XGBoost 利用泰勒展开式将损失函数展开到二阶，并利用二阶导数信息加快训练集的收敛速度

Bagging方法

是一种降低模型方差的集成学习方法，它通过随机抽取数据的方式，构建多个基模型，并将它们的结果进行集成，从而得到一个泛化能力更强的模型。Bagging方法有三种常见的算法：

决策树的Bagging

这种方法是基于决策树的Bagging，也称为树的聚合（Bagging of Tree）。它的基本思想是通过随机抽取数据和特征，构建多棵决策树，并将它们的结果进行集成。决策树具有显著的低偏差、高方差的特点，因此通过Bagging方法可以降低模型方差，提高模型的泛化能力。

随机森林算法

随机森林算法是一种基于决策树的Bagging方法，它在决策树的基础上引入了随机特征选择。具体来说，随机森林算法在每个节点上随机选择一部分特征进行划分，从而降低模型方差，提高模型的泛化能力。

极端随机森林算法

极端随机森林算法是一种基于决策树的Bagging方法，它在随机森林算法的基础上进一步引入了随机特征和随机阈值选择。具体来说，极端随机森林算法在每个节点上随机选择一部分特征和一个随机阈值进行划分，从而进一步降低模型方差，提高模型的泛化能力。

具体应用

“易速鲜花”运营部门提出了两个裂变思路。

方案一是选择一批热销商品，让老用户邀请朋友扫码下载 App 并成功注册，朋友越多，折扣越大。我们把这个方案命名为“疯狂打折”，它走的是友情牌。

方案二是找到一个朋友一起购买，第二件商品就可以免费赠送，这叫“买一送一”。具体来说，方案一是让老用户邀请朋友扫码下载 App 并成功注册，朋友越多，折扣越大。

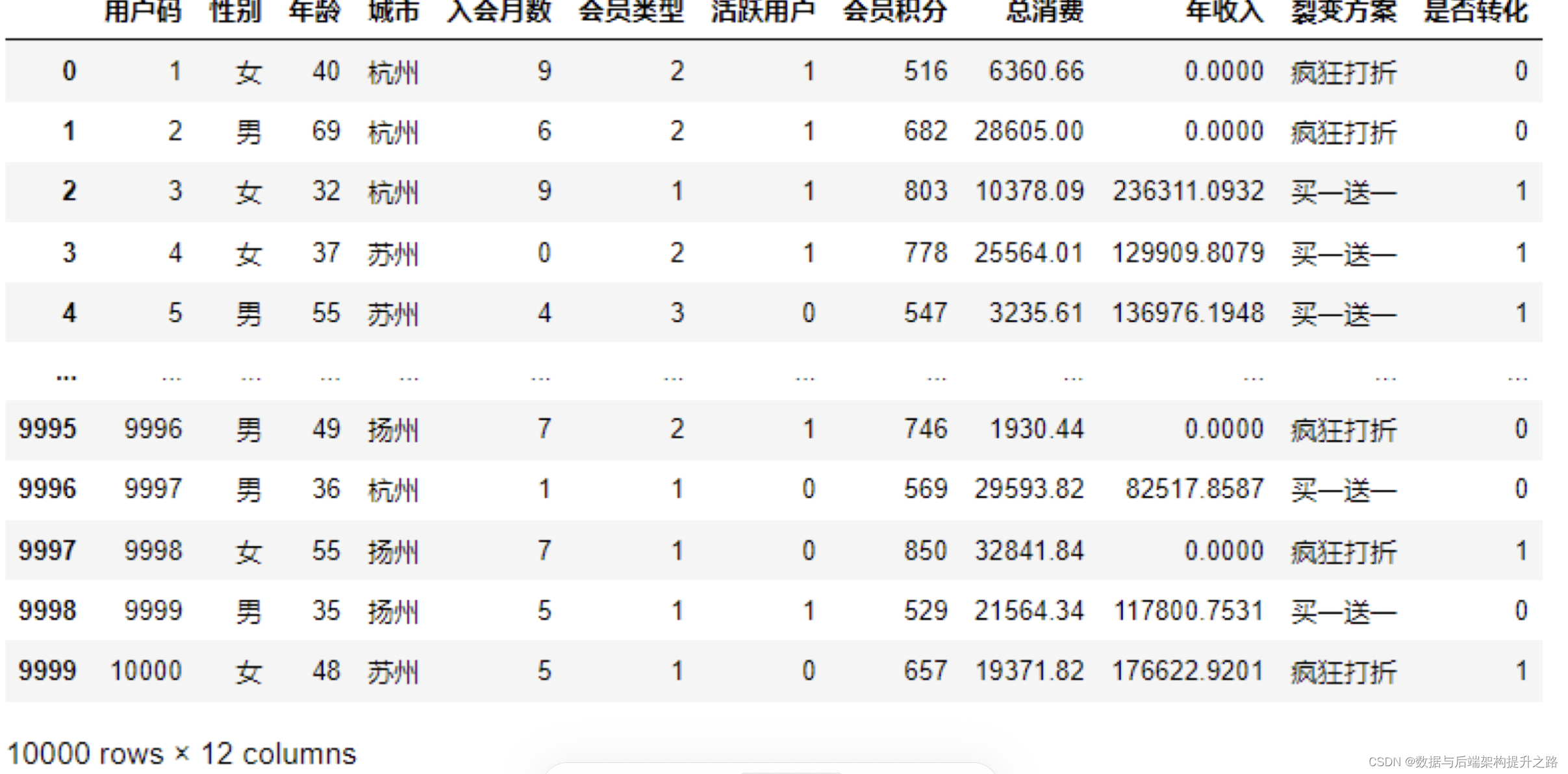
我们今天的目标就是根据这个数据集，来判断一个特定用户在特定的裂变促销之下，是否会转化。

预测代码如下：

import pandas as pd #导入Pandas
from sklearn.metrics import f1_score
from sklearn.tree import DecisionTreeClassifierdf_fission = pd.read_csv('易速鲜花裂变转化.csv') #载入数据
df_fission.head() #显示数据import matplotlib.pyplot as plt #导入pyplot模块
import seaborn as sns #导入Seaborn
fig = sns.countplot('是否转化', data=df_fission) #创建柱状计数图
fig.set_ylabel("数目") #Y轴标题
plt.show() #显示图像# 把二元类别文本数字化
df_fission['性别'].replace("女",0,inplace = True)
df_fission['性别'].replace("男",1,inplace=True)
# 显示数字类别
print("Gender unique values",df_fission['性别'].unique())
# 把多元类别转换成多个二元哑变量，然后贴回原始数据集
df_fission = pd.get_dummies(df_fission, drop_first = True)
df_fission # 显示数据集X = df_fission.drop(['用户码','是否转化'], axis = 1) # 构建特征集
y = df_fission.是否转化.values # 构建标签集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2)
from sklearn.preprocessing import MinMaxScaler #导入归一化缩放器
scaler = MinMaxScaler() #创建归一化缩放器
X_train = scaler.fit_transform(X_train) #拟合并转换训练集数据
X_test = scaler.transform(X_test) #转换测试集数据# 一、测试准确率是指在测试集上分类器正确分类的样本数占总样本数的比例。它是分类器性能的一个重要指标，但是它不能很好地反映分类器在不同类别上的表现。
#
#二、 F1分数是精确率和召回率的调和平均数，它综合了分类器的精确率和召回率，是一个更全面的分类器性能指标。
# 精确率是指分类器正确预测为正例的样本数占预测为正例的样本数的比例，召回率是指分类器正确预测为正例的样本数占实际为正例的样本数的比例。F
# 1分数越高，表示分类器的性能越好。#1.1 AdaBoost算法
from sklearn.ensemble import AdaBoostClassifier # 导入AdaBoost 模型
dt = DecisionTreeClassifier() # 选择决策树分类器作为AdaBoost 的基准算法
ada = AdaBoostClassifier(dt) # AdaBoost 模型
ada.fit(X_train, y_train) # 拟合模型
y_pred = ada.predict(X_test) # 进行预测
print("AdaBoost 测试准确率: {:.2f}%".format(ada.score(X_test, y_test)*100))
print("AdaBoost 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))# 1.2 GBDT算法
from sklearn.ensemble import GradientBoostingClassifier # 导入梯度提升模型
gb = GradientBoostingClassifier() # 梯度提升模型
gb.fit(X_train, y_train) # 拟合模型
y_pred = gb.predict(X_test) # 进行预测
print(" 梯度提升测试准确率: {:.2f}%".format(gb.score(X_test, y_test)*100))
print(" 梯度提升测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))#1.3 XGBoost算法
from xgboost import XGBClassifier # 导入XGB 模型
xgb = XGBClassifier() # XGB 模型
xgb.fit(X_train, y_train) # 拟合模型
y_pred = xgb.predict(X_test) # 进行预测
print("XGB 测试准确率: {:.2f}%".format(xgb.score(X_test, y_test)*100))
print("XGB 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))#2.1 决策树的Bagging
from sklearn.ensemble import BaggingClassifier # 导入Bagging 分类器
from sklearn.tree import DecisionTreeClassifier # 导入决策树分类器
from sklearn.metrics import (f1_score, confusion_matrix) # 导入评估指标
dt = BaggingClassifier(DecisionTreeClassifier()) # 只使用一棵决策树
dt.fit(X_train, y_train) # 拟合模型
y_pred = dt.predict(X_test) # 进行预测
print(" 决策树测试准确率: {:.2f}%".format(dt.score(X_test, y_test)*100))
print(" 决策树测试F1 分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
bdt = BaggingClassifier(DecisionTreeClassifier()) # 树的Bagging
bdt.fit(X_train, y_train) # 拟合模型
y_pred = bdt.predict(X_test) # 进行预测
print(" 决策树Bagging 测试准确率: {:.2f}%".format(bdt.score(X_test, y_test)*100))
print(" 决策树Bagging 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))#2.2 随机森林算法
from sklearn.ensemble import RandomForestClassifier # 导入随机森林模型
rf = RandomForestClassifier() # 随机森林模型
rf.fit(X_train, y_train) # 拟合模型
y_pred = rf.predict(X_test) # 进行预测
print(" 随机森林测试准确率: {:.2f}%".format(rf.score(X_test, y_test)*100))
print(" 随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))#2.3 极端随机森林算法
from sklearn.ensemble import ExtraTreesClassifier # 导入极端随机森林模型
ext = ExtraTreesClassifier() # 极端随机森林模型
ext.fit(X_train, y_train) # 拟合模型
y_pred = ext.predict(X_test) # 进行预测
print(" 极端随机森林测试准确率: {:.2f}%".format(ext.score(X_test, y_test)*100))
print(" 极端随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))