什么是散列表

散列表用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表。

我用一个例子来解释一下。假如我们有 89 名选手参加学校运动会。为了方便记录成绩，每个选手胸前都会贴上自己的参赛号码，用 6 位数字来表示，比如 051167，其中，前两位 05 表示年级，中间两位 11 表示班级，最后两位还是原来的编号 1 到 89。现在我们希望编程实现这样一个功能，通过编号快速找到对应的选手信息。你会怎么做呢？

我们可以把这 89 名选手参赛编号的后两位作为数组下标，来存取选手信息数据。当通过参赛编号查询选手信息的时候，取参赛编号的后两位，作为数组下标，来读取数组中的数据。

因为参赛编号后两位跟数组下标一一对应，当我们需要查询参赛编号为 x 的选手的时候，我们只需要将下标为 x 的数组元素取出来就可以了，时间复杂度就是 O(1)。

这就是典型的散列思想。其中，参赛选手的编号我们叫做键（key）或者关键字。我们用它来标识一个选手。我们把参赛编号转化为数组下标的映射方法就叫作散列函数（或“Hash 函数”“哈希函数”），而散列函数计算得到的值就叫作散列值（或“Hash 值”“哈希值”）。
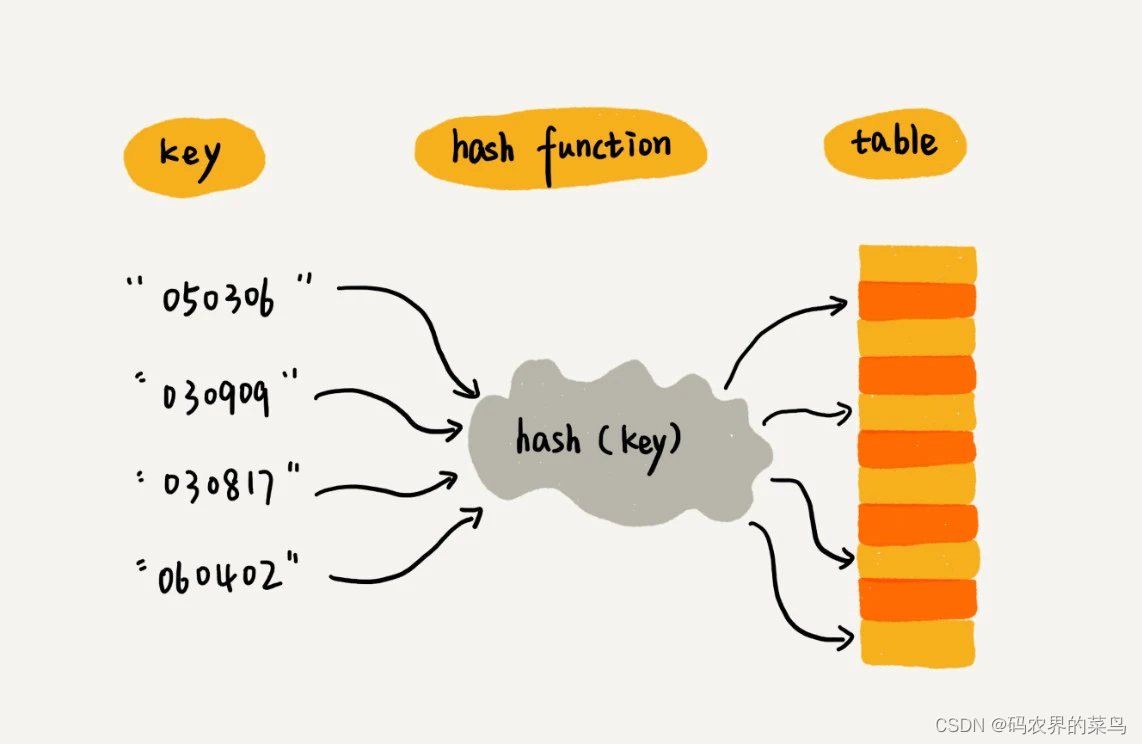
在这里插入图片描述
通过这个例子，我们可以总结出这样的规律：散列表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。

散列函数的设计原则

散列函数，顾名思义，它是一个函数。我们可以把它定义成 hash(key)，其中 key 表示元素的键值，hash(key) 的值表示经过散列函数计算得到的散列值。

那上面的例子，写成散列函数稍微有点复杂。我用伪代码将它写成函数就是下面这样：

int hash(String key) {// 获取后两位字符string lastTwoChars = key.substr(length-2, length);// 将后两位字符转换为整数int hashValue = convert lastTwoChas to int-type;return hashValue;
}

实际上开发过程中使用的散列函数一般不会像我们例子中的这样简单，一个散列函数的设计需要注意一下三点：

散列函数计算得到的散列值是一个非负整数；
如果 key1 = key2，那 hash(key1) == hash(key2)；
如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。

其中，第一点理解起来应该没有任何问题。因为数组下标是从 0 开始的，所以散列函数生成的散列值也要是非负整数。第二点也很好理解，相同的 key，经过散列函数得到的散列值也应该是相同的。第三点理解起来可能会有问题，我着重说一下。这个要求看起来合情合理，但是在真实的情况下，要想找到一个不同的 key 对应的散列值都不一样的散列函数，几乎是不可能的。即便像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突。而且，因为数组的存储空间有限，也会加大散列冲突的概率。

散列冲突的解决办法

再好的散列函数也无法避免散列冲突。那究竟该如何解决散列冲突问题呢？我们常用的散列冲突解决方法有两类，开放寻址法（open addressing）和链表法（chaining）。

1. 开放寻址法

开放寻址法的核心思想是，如果出现了散列冲突，我们就重新探测一个空闲位置，将其插入。那寻找新的空闲位置的方法又有线性探测、二次探测、双重散列等。

线性探测
当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。

举一个例子具体给你说明一下。这里面黄色的色块表示空闲位置，橙色的色块表示已经存储了数据。

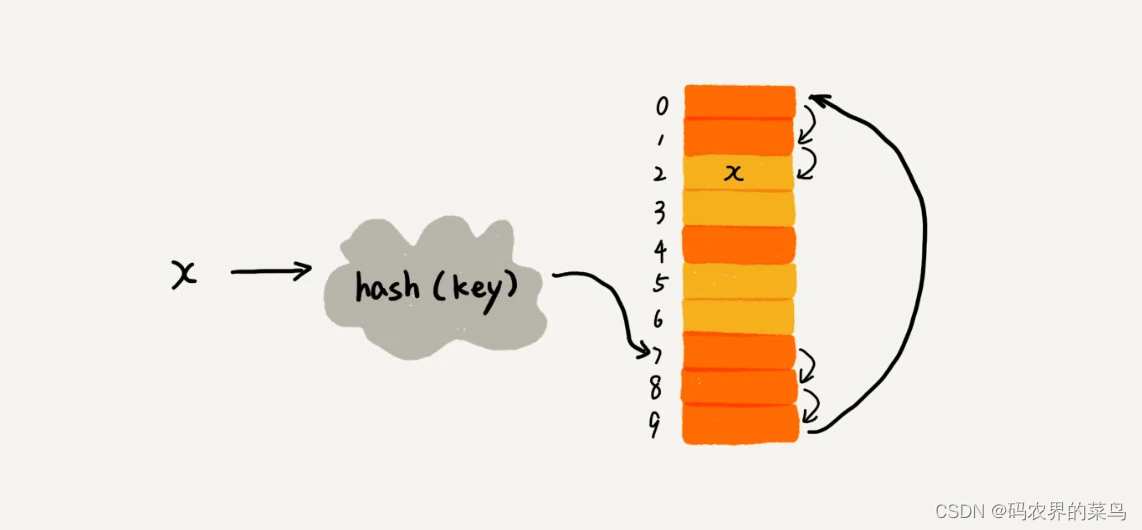
从图中可以看出，散列表的大小为 10，在元素 x 插入散列表之前，已经 6 个元素插入到散列表中。x 经过 Hash 算法之后，被散列到位置下标为 7 的位置，但是这个位置已经有数据了，所以就产生了冲突。于是我们就顺序地往后一个一个找，看有没有空闲的位置，遍历到尾部都没有找到空闲的位置，于是我们再从表头开始找，直到找到空闲位置 2，于是将其插入到这个位置。\
二次探测
二次探测，跟线性探测很像，线性探测每次探测的步长是 1，那它探测的下标序列就是 hash(key)+0，hash(key)+1，hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”，也就是说，它探测的下标序列就是 hash(key)+0，hash(key)+12，hash(key)+22……
双重散列
双重散列，意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key)，hash2(key)，hash3(key)……我们先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依次类推，直到找到空闲的存储位置。

不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子（load factor）来表示空位的多少。装载因子的计算公式是：

散列表的装载因子=填入表中的元素个数/散列表的长度

装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。

2. 链表法

链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多。我们来看这个图，在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。
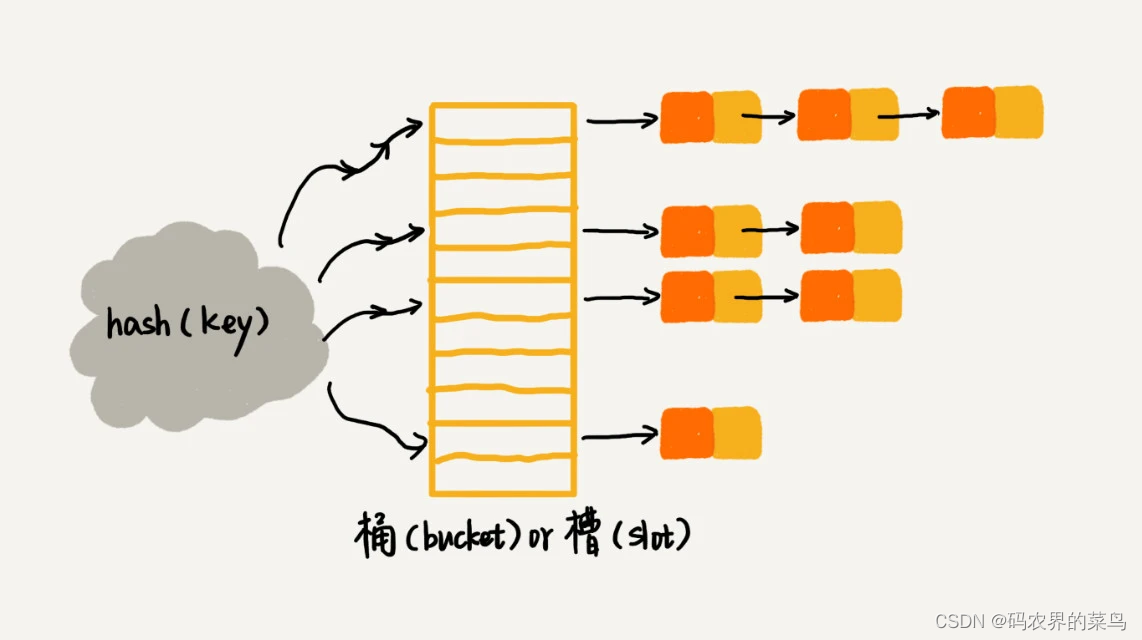
在这里插入图片描述
当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢？