法一：并查集

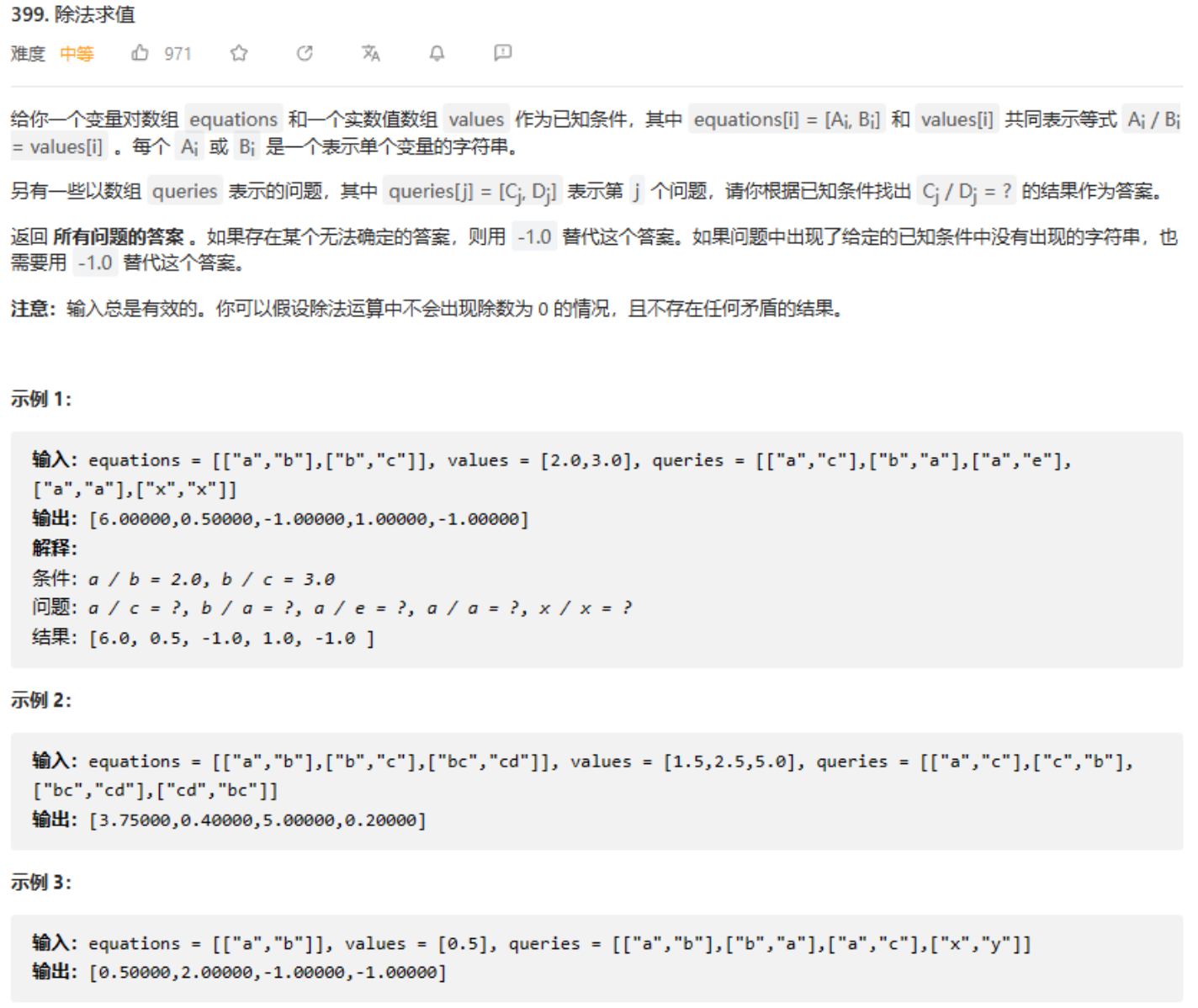
分析示例1：

• $a/b=2.0$，说明 $a=2b$，$a$和$b$在同一个集合中
• $b/c=3.0$，说明 $b=3c$，$b$和$c$在同一个集合中

求 $a/c$，可以把 $a=2b,b=3c$ 依次代入，得到 $a/c=\frac{2b}{c}=\frac{2\cdot 3c}{c}=6.0$

求 $b/a$，可以根据 $a=2b$ 知道 $b/a=0.5$，也可以把 $b$ 和 $a$ 都转换成 $c$ 的倍数，$b/a=\frac{b}{2b}=\frac{3c}{6c}=0.5$

我们计算了两个结果，不难知道：可以将题目给出的 equations 中的两个变量所在集合进行**「合并」**，同在一个集合中的两个变量就可以通过某种方式计算出它们的比值。具体来说，可以把不同的变量的比值转换成相同变量的比值，然后再计算转换成相同变量以后的系数的比值，即为结果。统一了比较的标准，可以以 $O(1)$ 的时间复杂度来完成计算。

如果两个变量不在一个集合中，返回 $-1.0$。并且根据题目的意思，如果两个变量中 至少有一个 变量没有出现在所有 equations 出现的字符集合中，也返回 $-1.0$。

构建有向图

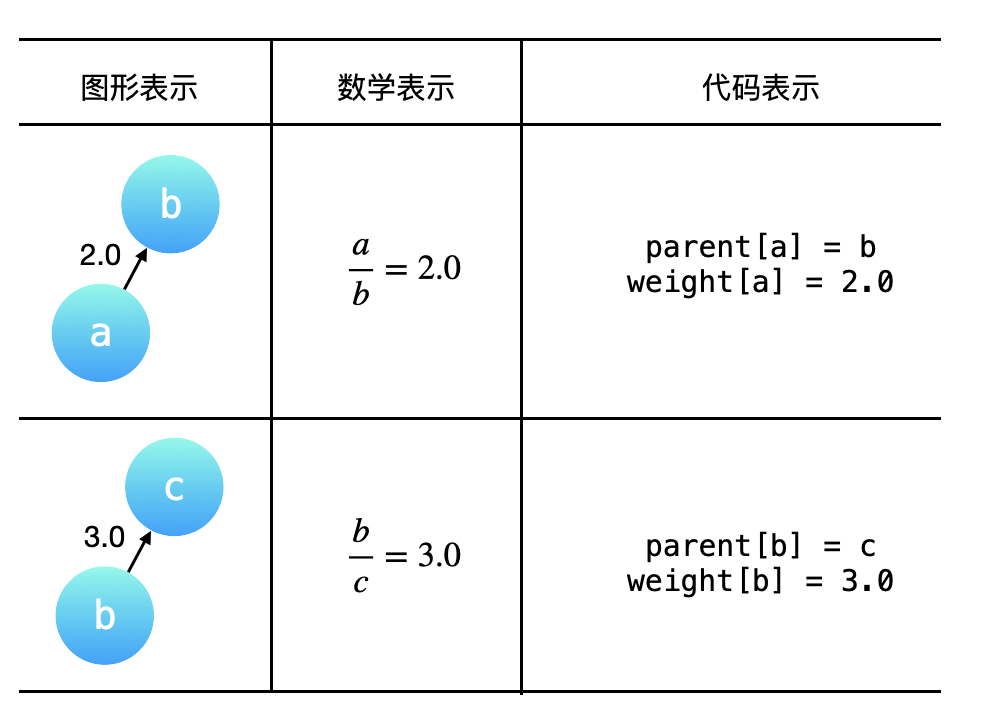
通过例1的分析，题目给出的 equations 和 values 可以表示成一个图，equations 中出现的变量就是图的顶点，「分子」与「分母」的比值可以表示成一个有向关系（因为「分子」和「分母」是有序的，不可以对换），并且这个图是一个带权图，values 就是对应的有向边的权值。

例 1 中给出的 equations 和 values 表示的「图形表示」、「数学表示」和「代码表示」如下表所示。

• 其中 parent[a] = b 表示：结点 a 的（直接）父亲结点是 b
• weight[a] = 2.0，即 weight[a] 表示结点 a 到它的 直接父亲结点 的有向边的权重

如何统一变量？

通过例1的分析，可以把 queries 中的不同变量转换成同一个变量，这样在计算 queries 的时候就可以用 $O(1)$ 的时间复杂度计算出结果，在「并查集」的一个优化技巧中，「路径压缩」就恰好符合了这样的应用场景。

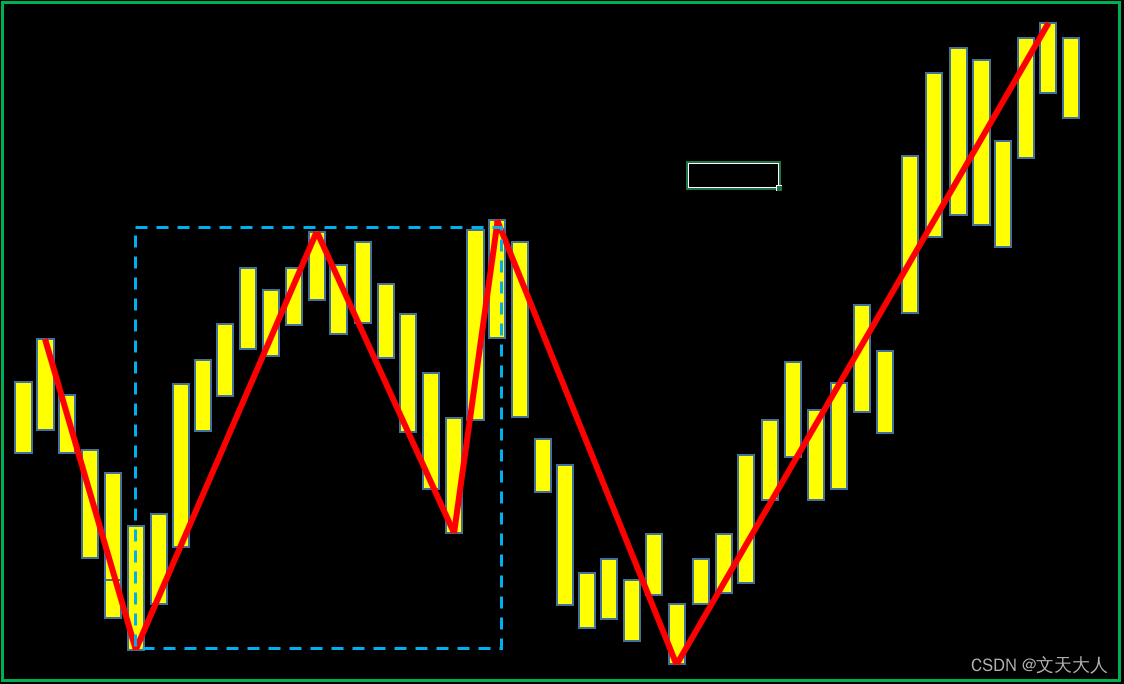
如下图所示：路径压缩前后，并查集所表示的两棵树形结构等价，路径压缩以后的树的高度为 2，查询性能最好。

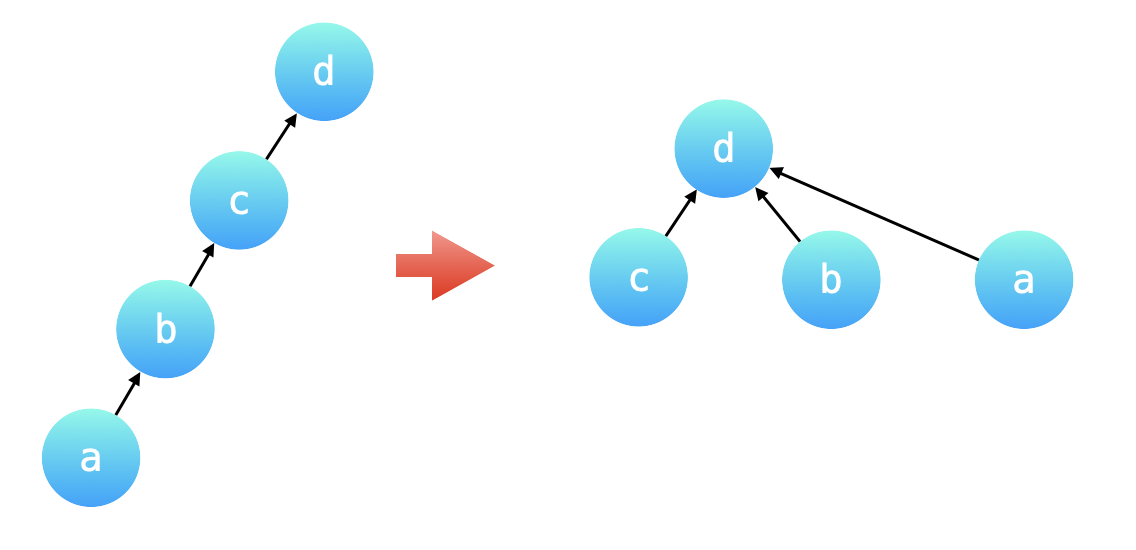
由于有「路径压缩」的优化，两个在一个连通分量中的不同变量，它们分别到根节点的权值的比值就是要求的结果。

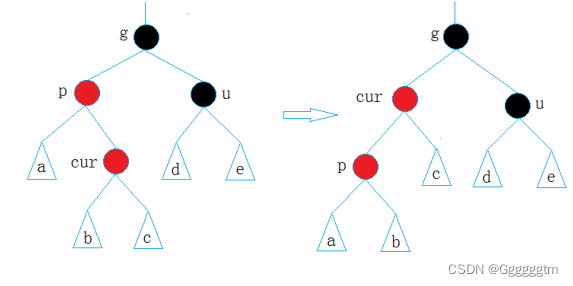
如何在「路径压缩」中维护权值变化？

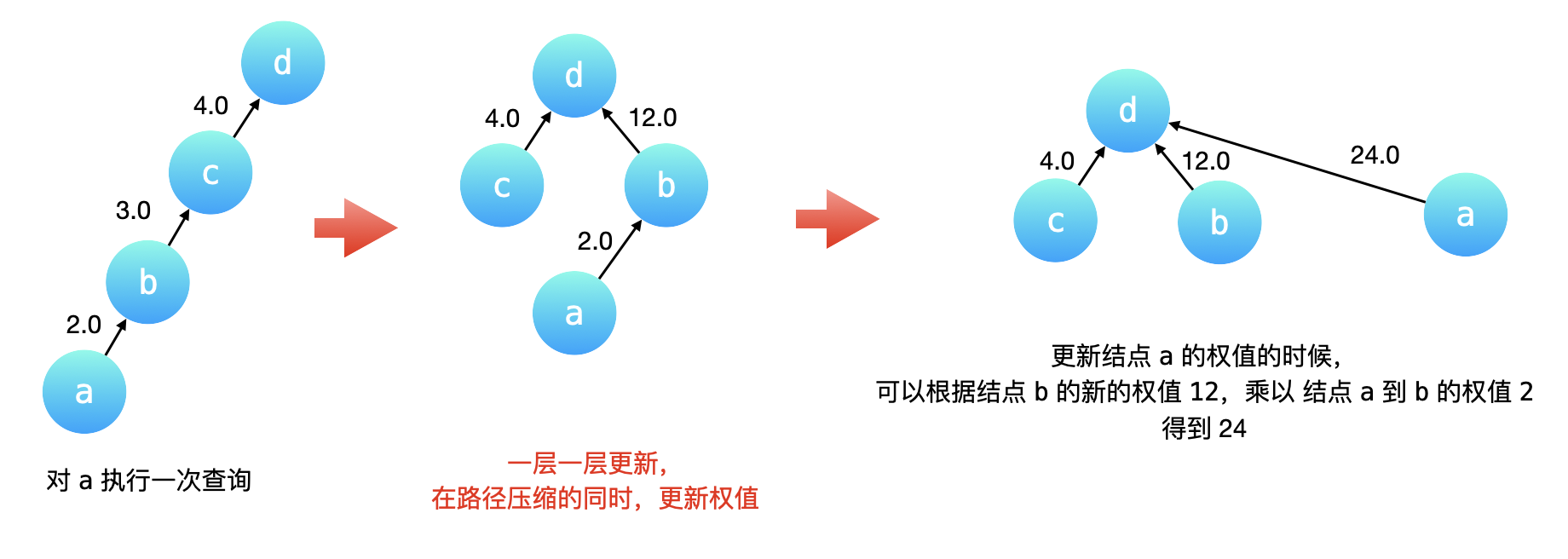
如下图所示，在结点a 执行一次「查询」操作。路径压缩会先一层一层向上先找到根结点 d，然后依次把 c、b、a 的父节点指向根节点 d。

• c 的父节点已经是根节点了，它的权值不用更改。
• b 的父节点要修改成根节点，它的权值就是从当前节点到根节点经过的所有有向边的权值的乘积。
• a 的父节点也要修改成根节点，但没必要把三条有向边的权值乘起来，可以直接用更新后的 b 到 d 的权值乘以 a 到 b 的权值。

如何在「合并」操作中维护权值的变化？

「合并」操作基于这样一个前提：将要合并的两棵树的高度最多为2，就是两棵树都必须要经过「路径压缩」。

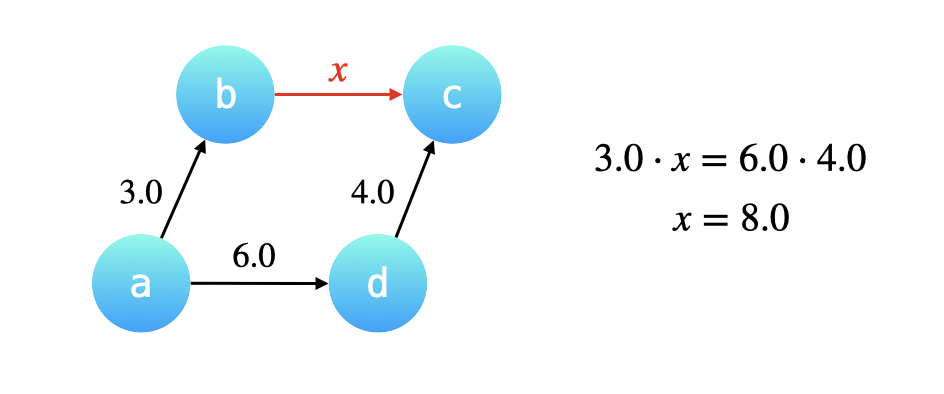
例如：已知 $a/b=3.0,d/c=4.0,a/d=6.0$，现在合并节点 a 和 d 所在的集合，其实就是把 a 的根节点 b 指向 d 的根节点 c，那么如何计算 b 指向 c 的这条有向边的权重呢？

根据 a 经过 b 可以到达 c，a 经过 d 也可以到达 c，因此两条路径上的有向边的权值的乘积必定相等。因此根据等式可求得 $b/c=\frac{\frac{a}{d}\cdot \frac{d}{c}}{\frac{a}{b}}$。

一个小细节

在合并以后，产生了一棵高度为 3 的树，那么我们在执行查询的时候，例如下图展示的绿色结点和黄色结点，绿色结点并不直接指向根结点，在计算这两个变量的比值的时候，计算边的权值的比值得到的结果是不对的。

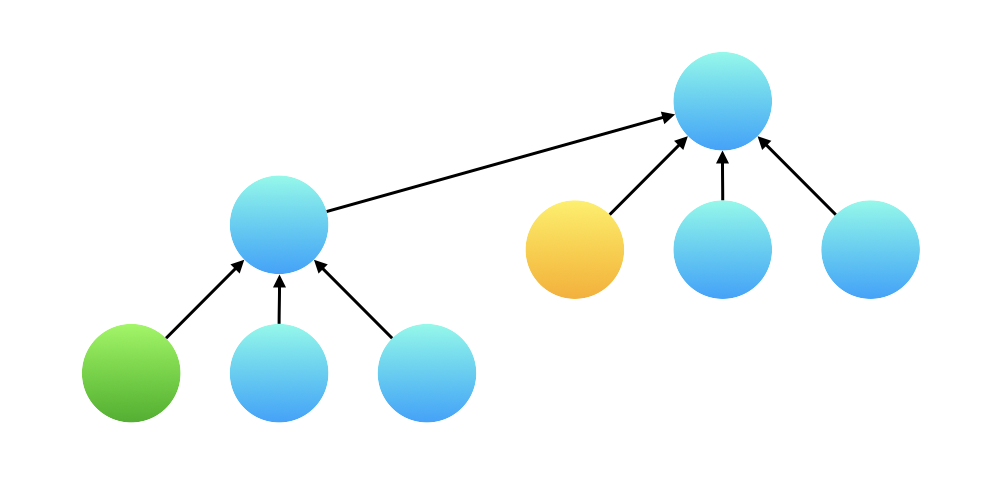
但其实不用担心这个问题，并查集的「查询」操作会执行「路径压缩」，所以真正在计算两个变量的权值的时候，绿色结点已经指向了根结点，和黄色结点的根结点相同。因此可以用它们指向根结点的有向边的权值的比值作为两个变量的比值。

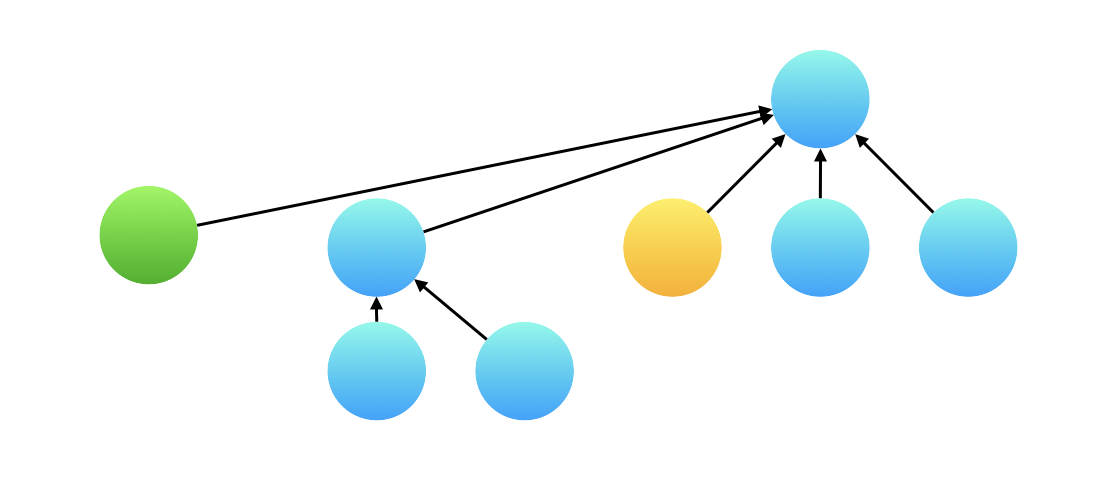
我们通过这个细节向大家强调：一边查询一边修改结点指向是并查集的特色。

代码

#include <vector>
#include <unordered_map>
#include <string>
using namespace std;class UnionFind{										//并查集类
private:vector<int> parent;vector<double> weight;      						//指向父节点的权重public:UnionFind(int n){        							//初始化，节点指向自己，初始权重为1.0parent = vector<int>(n);weight = vector<double>(n);for(int i = 0; i < n; i++){parent[i] = i;weight[i] = 1.0;}}int find(int x){                                	//带路径压缩的查找if(x != parent[x]){				 				//x节点不为根节点int origin = parent[x];						//记录父节点parent[x] = find(parent[x]);				//递归向上查找父节点weight[x] *= weight[origin];				//将路径上的权重相乘}return parent[x];}void unite(int x, int y, double value){				//合并int rootX = find(x), rootY = find(y);			//查找过程中已经进行过路径压缩if(rootX == rootY)								//若在同一集合，直接返回return;parent[rootX] = rootY;							//合并操作weight[rootX] = weight[y] * value / weight[x];	//value=a/d,weight[y]=d/c,weight[x]=a/b}double isConnected(int x, int y){					//计算x/y的结果int rootX = find(x);int rootY = find(y);if(rootX == rootY)								//若为同一集合，则直接相除即为结果return weight[x] / weight[y];else											//若不为同一集合，说明问题中有未知变量return -1.0;}
};class Solution{
public:vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {int equationsSize = equations.size();UnionFind unionFind(2 * equationsSize);//第一步：预处理，将变量的值转换为数字（并查集），使得并查集的底层使用数组实现，方便编码unordered_map<string, int> hashMap(2 * equationsSize);int id = 0;for(int i = 0; i < equationsSize; i++){string var1 = equations[i][0];string var2 = equations[i][1];if(hashMap.count(var1) == 0){hashMap[var1] = id++;}if(hashMap.count(var2) == 0){hashMap[var2] = id++;}unionFind.unite(hashMap[var1], hashMap[var2], values[i]);	//将所有集合合并 var1/var2}//第二步：查询int queriesSize = queries.size();vector<double> res(queriesSize, -1.0);							//存储结果for(int i = 0; i < queriesSize; i++){string var1 = queries[i][0];string var2 = queries[i][1];if(hashMap.count(var1) && hashMap.count(var2)){				//变量在条件中出现，计算结果int id1 = hashMap[var1];int id2 = hashMap[var2];res[i] = unionFind.isConnected(id1, id2);}}return res;}
};