逻辑回归算法
- 简介
- 逻辑回归与条件概率
- 绘制sigmoid函数
简介
逻辑回归算法是一种简单但功能强大的
二元线性分类算法。需要注意的是,尽管"逻辑回归"名字带有“回归”二字,但逻辑回归是一个分类算法,而不是回归算法。
我认为,逻辑回归算法功能强大的原因,更在于,它不仅仅可以预测类别标签,而且还可以预测类别的概率。
比如说,使用逻辑回归预测天气,不仅仅可以预测某一天是否会下雨,还可以给出下雨的概率。类似地,也可以使用逻辑回归算法来预测症状给定的情况下患者患有某种疾病的概率,这也是逻辑回归在医学领域广受欢迎的原因。
逻辑回归与条件概率
逻辑回归是一个二元分类概率模型。下面我们主要了解一下逻辑回归背后的主要机制。
p \ p p:感兴趣事件发生的概率(所谓感兴趣,正是我们想要预测的事件,比如患者在出现某些症状时患病的概率。)
几率(odds):是一个事件发生可能性的度量。数学表达式为: p 1 − p \frac{p}{1-p} 1−pp.
logit 函数:logit函数是几率(odds)的对数函数:
l o g i t ( p ) = log p 1 − p \ logit(p)=\log \frac{p}{1-p} logit(p)=log1−pp
这里的log是自然对数。logit函数的输入即p是一个介于0-1之间的正数,输出即logit§为任意实数。
那如何将这里的输出将我们的数据相联系起来呢?
我们假设我们的输出即logit§与每一个样本的特征值 x 1 x 2 x 3 . . . x m \ x_1 x_2 x_3...x_m x1x2x3...xm的加权( w T \ w^T wT)和加偏置顶存在线性关系,即:
l o g i t ( p ) = w 1 x 1 + w 2 x 2 + . . . . . . + w m x m + b = ∑ j = 1 m w j x j + b = w T x + b logit(p)=w_1x_1+w_2x_2+......+w_mx_m+b=\sum_{j=1}^mw_jx_j+b=w^Tx+b logit(p)=w1x1+w2x2+......+wmxm+b=∑j=1mwjxj+b=wTx+b
当我们真正感兴趣的是条件概率 p p p,即在给定一个样本特征的前提下求解类别标签为1的概率。
通过logit函数,我们可以将条件概率p映射为一个实数。那反过来,我们要求p的话呢?所以,我们可以根据logit函数求解出它的逆函数。
logit函数的逆函数通常称为logistic sigmoid函数。由于这个函数具有S形状,因此有时也简称为sigmoid函数:
σ ( z ) = 1 1 = e − z \sigma(z)=\frac{1}{1=e^{-z}} σ(z)=1=e−z1
这里z是净输入,为样本的加权和加偏置顶:
z = w T x + b z=w^Tx+b z=wTx+b
绘制sigmoid函数
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):return 1.0/(1.0+np.exp(-z))
z=np.arange(-7,7,0.1)
sigma_z=sigmoid(z)
plt.plot(z,sigma_z)
plt.axvline(0.0,color='k')
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\sigma(z)$')
plt.yticks([0.0,0.5,1.0])
ax=plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()
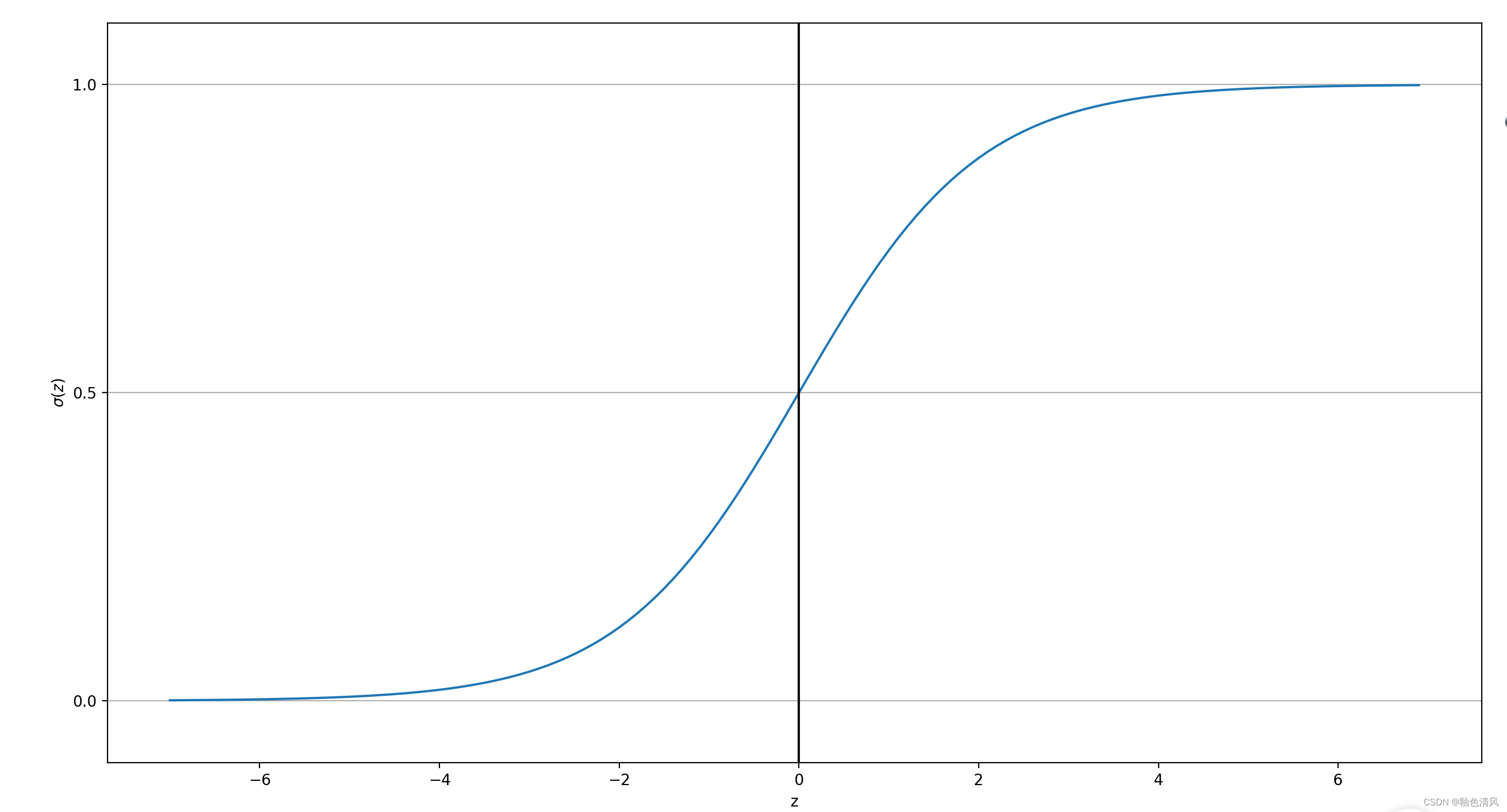
但输入的 z z z为0时,输出p为0.5。当输入的z趋近于 + ∞ + \infty +∞时,输出p接近于1。当输入的趋近于 − ∞ - \infty −∞时,输出p接近于1。
而且当输入的 z > 0 z>0 z>0,那么p>0.5,可以判别是预测事件的发生。当 z < 0 z<0 z<0时,可以认为是预测事件的不发生。即对应的二值输出为:
y ^ = { 1 如果 σ ( z ) ≥ 0.5 0 其他 \widehat{y}=\begin{cases} 1 如果\sigma(z)≥0.5\\ 0 其他 \end{cases} y ={1如果σ(z)≥0.50其他