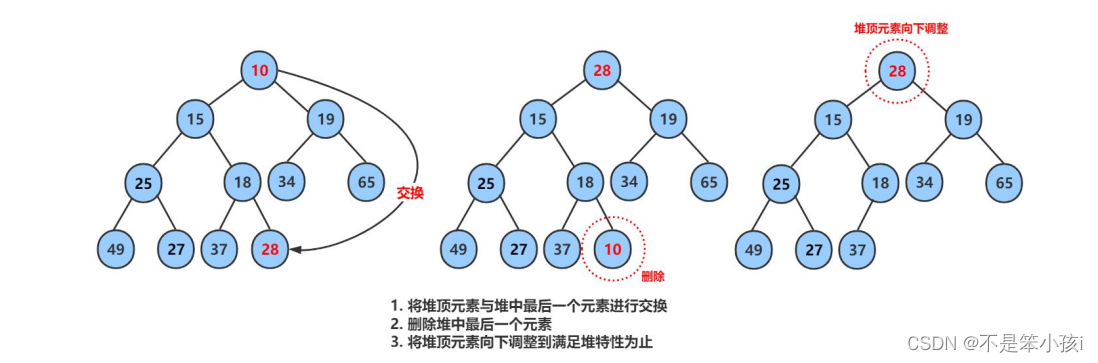
文章目录
- 前言
- 三、广义积分
- 3.1 敛散性概念
- (一)积分区间为无限的广义积分
- (二)积分区间有限但存在无穷间断点
- 3.2 敛散性判别法
- 四、定积分应用
- 写在最后
前言
承接前文,梳理完定积分的定义及性质后,我们进入广义积分的学习。
通过可积的概念我们可以清楚,连续函数是可积的,同时,有有限个第一类间断点的函数也是可积的。这类积分积分区间是有限的,称为正常积分。而如果出现 积分区间无限(如上限为无穷等)或被积函数在积分区间内有无穷间断点,称这类积分为广义积分或反常积分。
三、广义积分
3.1 敛散性概念
(一)积分区间为无限的广义积分

实际进行判断时,我们一般直接写成原函数相减的形式。如: ∫ 1 ∞ x 1 + x 4 d x = 1 2 a r c t a n x ∣ 1 ∞ = 1 2 ( π 2 − π 4 ) = π 8 \int_1^{\infty}\frac{x}{1+x^4}dx=\frac{1}{2}arctanx \big| _1^{\infty}=\frac{1}{2}(\frac{\pi}{2}-\frac{\pi}{4})=\frac{\pi}{8} ∫1∞1+x4xdx=21arctanx 1∞=21(2π−4π)=8π
这里补充一个 Γ \Gamma Γ 函数,其定义为: Γ ( α ) = ∫ 0 ∞ x α − 1 e − x d x ( α > 0 ) \Gamma(\alpha)=\int_0^{\infty}x^{\alpha -1}e^{-x}dx (\alpha>0) Γ(α)=∫0∞xα−1e−xdx(α>0) 主要有如下性质: Γ ( α + 1 ) = α Γ ( α ) , Γ ( n + 1 ) = n ! , Γ ( 1 2 ) = π . \Gamma(\alpha+1)=\alpha \Gamma(\alpha),\Gamma(n+1)=n!, \Gamma(\frac{1}{2})= \sqrt{\pi}. Γ(α+1)=αΓ(α),Γ(n+1)=n!,Γ(21)=π.

定义 2 是当下限为无穷时的广义积分,和第一种情况类似。

当上下限均为无穷时,需要将区间分为两部分,分别进行收敛性判断,且最后的积分为两部分积分之和。
(二)积分区间有限但存在无穷间断点
定义 4 —— 设 f ( x ) ∈ C ( a , b ] f(x) \in C(a,b] f(x)∈C(a,b] 且 f ( a + 0 ) = ∞ f(a+0)=\infty f(a+0)=∞ ,对 ∀ ϵ > 0 \forall \epsilon>0 ∀ϵ>0 ,记 ∫ a + ϵ b f ( x ) d x = F ( b ) − F ( a + ϵ ) ; \int_{a+\epsilon}^bf(x)dx=F(b)-F(a+\epsilon); ∫a+ϵbf(x)dx=F(b)−F(a+ϵ); 若上述极限存在,则广义积分 ∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx 收敛,且等于该极限值。
若上述极限不存在,则广义积分 ∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx 发散。
同样,当在 b 处无穷间断或区间中其他点无穷间断时,分别有如下定义。


3.2 敛散性判别法
针对各种类型的广义积分,分别有不同的判别法,但彼此之间的形式较为相似。

除此以外,广义积分还有判别定理,有点儿级数收敛的意思了。

四、定积分应用
定积分在几何上的应用有求面积,包括旋转曲面的面积和一些曲线所围的面积等。还有求体积,如绕某条坐标轴旋转一周的体积。求曲线长度,如各种坐标系下曲线的长度。
定积分在物理上的应用主要为求做功和受力。
在具体求解时,关键是掌握好微元法的思想,先找到一个小微元 [ x , x + d x ] [x,x+dx] [x,x+dx] 。求面积则把面积的表达式写出来,如 d A = x d x dA=xdx dA=xdx 。求体积则把体积表示出来,如 d V = π x 2 d x dV=\pi x^2dx dV=πx2dx 。求压力,则把压力表示出来,如 d F = e g h ⋅ d S dF=egh\cdot dS dF=egh⋅dS 。
写出来后根据积分区间进行定积分求解即可,如 V = ∫ d V = ∫ π x 2 d x V=\int dV=\int \pi x^2dx V=∫dV=∫πx2dx 。
写在最后
定积分的内容多啊,任重道远,后面还有重积分、曲线、曲面积分等等。不过只要坚持把这块啃下来,后面的进度就会好一些。




![NLP文本匹配任务Text Matching [无监督训练]:SimCSE、ESimCSE、DiffCSE 项目实践](https://img-blog.csdnimg.cn/img_convert/44d419b05793d534eec259bf37dde5f9.png)