割点
定义
割点的定义:如果一个点被删除之后会导致整个图不再是一个连通图,那么这个顶点就是这个图的割点。举例:
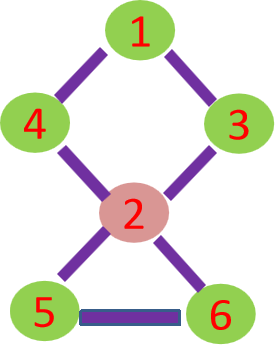
上图中的点2就是一个割点,如果它被删除,则整个图被分为两个连通分量,不再是一个连通图。
求割点的方法
最直观容易想到的一种简单朴素的方法:
依次删除每一个顶点,然后用dfs或者bfs来检查图是否依然连通。如果删除某个顶点后,导致图不再连通,那么刚才删除的顶点就是割点。
这种方法的时间复杂度是O(N(N+M))。显然不是一个高性能的算法。
考虑更高性能的算法:
考虑从根节点开始进行DFS遍历,遍历的同时记录每个节点的遍历顺序(又称为时间戳)到数组num。如下图:
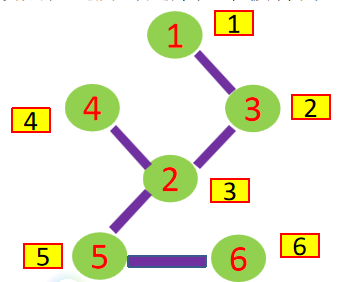
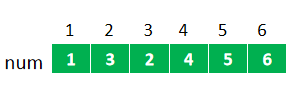
圆圈中数字是顶点编号, 圆圈右上角的数表示这个顶点的“时间戳” 。
那么在遍历过程中如何判断割点?见下表:
| 节点类型 | 判断方法 | 解释 |
|---|---|---|
| 根节点 | 对于根节点,有两棵及以上不相连的子树,则根节点是割点 | 很显然如果根节点有两棵及以上的不相连的子树,那么根节点被删除之后整个图将会不再是一个连通图,会被划分为多个连通块。 |
| 非根节点 | 对于非根节点,u的直接子v或者v的后代没有回退到u的祖先的边(没有不经过u直接回到u的祖先的路径),则u不是割点,否则是。 | 如果非根节点u的子节点v及v的后代节点有路径可以不经过点u回退到u的祖先,那么这个点即使被删除,整个图依然是连通的。 |
那么该算法具体如何实现呢?
定义一个数组low来记录每个顶点在不经过父顶点时,能够回到的最小“时间戳”。
对于某个顶点u,如果存在至少一个顶点v(u的儿子),使得low[v]>=num[u],即不能退回到祖先,顶多退回到顶点u,那么u点为割点。
示例代码(POJ1144)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e2 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
int num[maxn]; // 记录每个点的dfs遍历顺序
int low[maxn]; // low[v]记录v和v的后代能连回到的祖先的num
int dfn; // 记录进入递归的顺序(也称为时间戳)
bool isCut[maxn]; // 标记割点
vector<int> G[maxn];void dfs(int u, int fa) { // 当前节点u,u的父节点falow[u] = num[u] = ++dfn; // 记录该点的遍历顺序,该点的low值初始等于numint child = 0; // 子树数目for (int i = 0; i < G[u].size(); i++) { // 处理u的所有子节点int v = G[u][i];if (!num[v]) { // v没访问过child++;dfs(v, u);low[u] = min(low[u], low[v]); // 用后代的返回值更新low值,从v以及v的后代可以回退到的祖先的num值if (low[v] >= num[u] && u != 1) { // 对于非根节点,u的直接子v或者v的后代没有回退到u的祖先的边,则u是割点isCut[u] = true;}} else if (num[v] < num[u] && v != fa) { // 处理回退边low[u] = min(low[u], num[v]);}}if (u == 1 && child >= 2) { // 对于根节点,有两棵以上不相连的子树,则根节点是割点isCut[1] = true;}
}void solve() {int n, ans;while (cin >> n, n) {if (n == 0)break;memset(low, 0, sizeof low);memset(num, 0, sizeof num);dfn = 0;for (int i = 1; i <= n; i++) {G[i].clear();}int a, b;while (cin >> a, a) {while (cin.get() != '\n') {cin >> b;G[a].push_back(b);G[b].push_back(a);}}memset(isCut, 0, sizeof isCut);ans = 0;dfs(1, 1);for (int i = 1; i <= n; i++) {ans += isCut[i];}cout << ans << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout << fixed;cout.precision(18);solve();return 0;
}割边
定义
如果在一个无向图中删除某条边后,图不再连通,那么这条边叫做割边(又称桥)。举例:
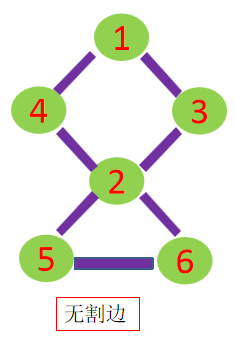
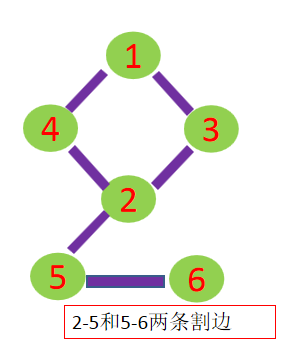
求割边的方法
只需将求割点的算法修改一个符号就可以。 只需将low[v]>=num[u]改为low[v]>num[u]。
这是为什么呢?
low[v]和num[u]相等则表示还可以回到父亲结点; 而low[v]>num[u]则表示连父亲都回不到了。倘若顶点v不能回到祖先,也没有另外的路能回到父亲,那么 u-v 这条边就是割边。
割边代码
……后边补上……
注:本文的部分内容和图片参考了 https://www.cnblogs.com/ljy-endl/p/11595161.html