👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——注意力分数(详细数学推导+代码实现)
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
自注意力和位置编码
- 引入
- 自注意力
- 多头注意力
- 基于多头注意力实现自注意力
- 比较CNN、RNN和self-attention
- 结论
- 剖析——CNN
- 剖析——RNN
- 剖析——self-attention
- 总结
- 位置编码
- 绝对位置信息
- 相对位置信息
- 小结
引入
在深度学习中,经常使用CNN和RNN对序列进行编码。有了自注意力之后,我们将词元序列输入注意力池化中,以便同一组词元同时充当查询、键和值。具体来说,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为自注意力(self-attention)。下面将使用自注意力进行序列编码。
import math
import torch
from torch import nn
from d2l import torch as d2l
自注意力
给定一个由词元组成的序列:
x 1 , . . . , x n 其中任意 x i ∈ R d x_1,...,x_n\\ 其中任意x_i∈R^d x1,...,xn其中任意xi∈Rd
该序列的自注意力输出为一个长度相同的序列:
y 1 , . . . , y n 其中 y i = f ( x i , ( x 1 , x 1 ) , . . . , ( x n , x n ) ) ∈ R d y_1,...,y_n\\ 其中y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))∈R^d y1,...,yn其中yi=f(xi,(x1,x1),...,(xn,xn))∈Rd
自注意力就是这样,任意的xi都是既当key,又当value,还当query。
下面的代码片段是基于多头注意力对一个张量完成自注意力的计算,张量形状为(批量大小,时间步数目或词元序列长度,d)。输出与输入的张量形状相同。
而在此之前,简单讲解下多头注意力,接着基于多头注意力实现自注意力。
多头注意力
当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习到不同的行为,然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系。因此允许注意力机制组合使用查询、键和值的不同子空间表示是有益的。
因此,与其只使用一个注意力池化,我们可以独立学习得到h组不同的线性投影来变换查询、键和值。然后,这h组变换后的查询、键和值将并行地送到注意力池化中。最后将这h个注意力池化的输出拼接在一起,并通过另一可以学习的线性投影进行变换,来产生最终输出。这就是多头注意力(multihead attention),如下图所示:
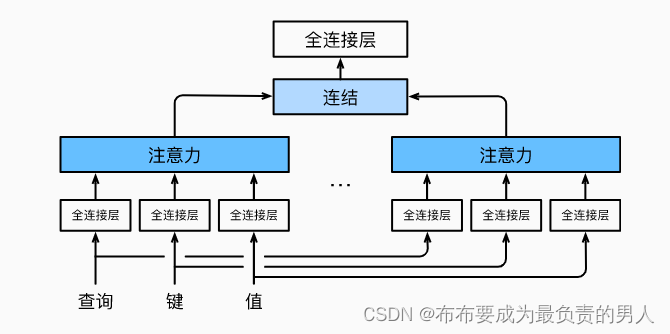
而多头注意力的实现过程通常使用的是缩放点积注意力来作为每一个注意力头,我们设定:
p q = p k = p v = p o / h p_q=p_k=p_v=p_o/h pq=pk=pv=po/h
值得注意的是,如果将查询、键和值的线性变化的输出数量设置为:
p q h = p k h = p v h = p o p_qh=p_kh=p_vh=p_o pqh=pkh=pvh=po
就可以并行计算h个头,下面代码中的po是通过num_hiddens指定的。
代码如下:
#@save
class MultiHeadAttention(nn.Module):"""多头注意力"""def __init__(self, key_size, query_size, value_size, num_hiddens,num_heads, dropout, bias=False, **kwargs):super(MultiHeadAttention, self).__init__(**kwargs)self.num_heads = num_headsself.attention = d2l.DotProductAttention(dropout)self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)def forward(self, queries, keys, values, valid_lens):# queries,keys,values的形状:# (batch_size,查询或者“键-值”对的个数,num_hiddens)# valid_lens 的形状:# (batch_size,)或(batch_size,查询的个数)# 经过变换后,输出的queries,keys,values 的形状:# (batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)queries = transpose_qkv(self.W_q(queries), self.num_heads)keys = transpose_qkv(self.W_k(keys), self.num_heads)values = transpose_qkv(self.W_v(values), self.num_heads)if valid_lens is not None:# 在轴0,将第一项(标量或者矢量)复制num_heads次,# 然后如此复制第二项,然后诸如此类。valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)# output的形状:(batch_size*num_heads,查询的个数,# num_hiddens/num_heads)output = self.attention(queries, keys, values, valid_lens)# output_concat的形状:(batch_size,查询的个数,num_hiddens)output_concat = transpose_output(output, self.num_heads)return self.W_o(output_concat)#@save
def transpose_qkv(X, num_heads):"""为了多注意力头的并行计算而变换形状"""# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,# num_hiddens/num_heads)X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)X = X.permute(0, 2, 1, 3)# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)return X.reshape(-1, X.shape[2], X.shape[3])#@save
def transpose_output(X, num_heads):"""逆转transpose_qkv函数的操作"""X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])X = X.permute(0, 2, 1, 3)return X.reshape(X.shape[0], X.shape[1], -1)
基于多头注意力实现自注意力
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,num_hiddens, num_heads, 0.5)
attention.eval()
可以输出验证一下:
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
print(attention(X, X, X, valid_lens).shape)
输出结果:
torch.Size([2, 4, 100])
比较CNN、RNN和self-attention
首先看这个图:
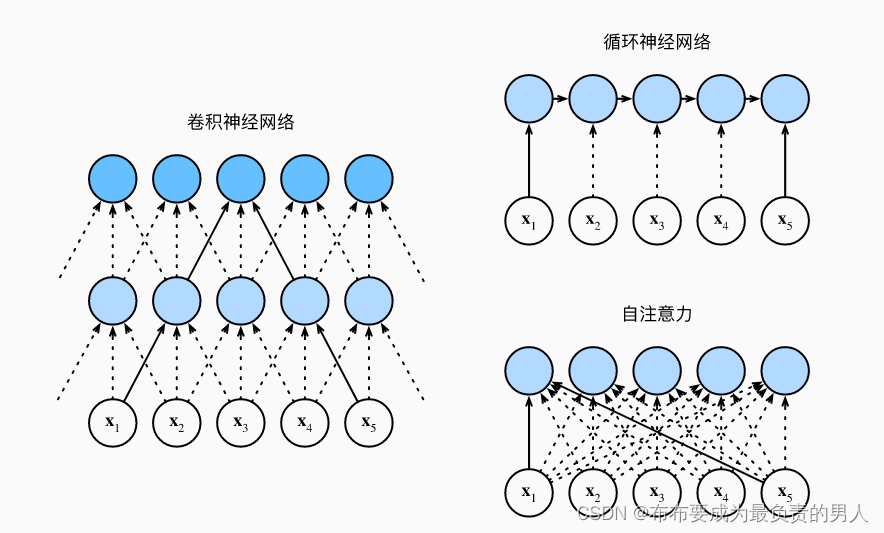
接下来进行CNN、RNN以及self-attention三个架构的比较,首先这三个架构目标都是要将n个词元组成的序列映射到另一个长度相同的序列,其中的每个输入词元或输出词元都由d维向量表示。我们的比较将基于计算的复杂性、顺序操作和最大路径长度,先给出结论再进行剖析解释。
我们首先要知道,顺序操作会妨碍并行计算,而任意的序列位置组合之间的路径越短,则能更轻松地学习序列中的远距离依赖关系。
结论
| 计算复杂度 | 并行度 | 最大路径长度 | |
|---|---|---|---|
| CNN | O(knd2) | O(n) | O(n/k) |
| RNN | O(nd2) | O(1) | O(n) |
| self-attention | O(n2d) | O(n) | O(1) |
剖析——CNN
考虑一个卷积核大小为k的卷积层,由于序列长度是n,输入和输出的通道数量都是d,所以卷积层的计算复杂度为O(knd2)。而如上图所示,可以看出CNN网络是分层的,因此会有O(1)个顺序操作,那么这代表着通道可以并行执行n个词元,那么并行度就是O(n)。
上图中可以看出k=3,因为这样刚好就使得x1和x5处于这个卷积核大小为3的双层卷积神经网络的感受野内。因此最大的路径长度一定是不会超过n/k的,下标为n的也会因为卷积核被限制到一个感受野内,因此可以知道最大路径长度为O(n/k)。
剖析——RNN
当更新RNN的隐状态时,d×d权重矩阵和d维隐状态的乘法计算复杂度为O(d2),再加上序列长度为n,因此RNN的计算复杂度为O(nd2),由上图也可以看出n个序列的顺序操作是没办法并行化的,则并行度为O(1),最大路径长度是O(n)(可以理解成当我们要组合y1和yn的时候,这时候长度为n)。
剖析——self-attention
查询、键、值都是n×d矩阵。计算过程为:n×d矩阵乘以d×n矩阵,之后得到的n×n矩阵再乘以n×d矩阵,因此自注意力有O(n2d)的计算复杂度。而上图展示了自注意力的强大,O(n)的并行度显而易见,同时最大路径长度是O(1),因为他们可以任意组合。
总结
总而言之,卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。
但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,通过在输入表示中添加位置编码来注入绝对的或相对的位置信息。
位置编码可以通过学习得到也可以直接固定得到,下面讲解基于正弦函数和余弦函数的固定位置编码。
假设输入表示X∈Rn×d包含一个序列中n个词元的d维嵌入表示。位置编码使用相同形状的位置嵌入矩阵P∈Rn×d输出X+P,矩阵第[i,2j](偶数列)和[i,2j+1](奇数列)列上的元素为:
p i , 2 j = s i n ( i 1000 0 2 j / d ) , p i , 2 j + 1 = c o s ( i 1000 0 2 j / d ) p_{i,2j}=sin(\frac{i}{10000^{2j/d}}),\\ p_{i,2j+1}=cos(\frac{i}{10000^{2j/d}}) pi,2j=sin(100002j/di),pi,2j+1=cos(100002j/di)
看起来很奇怪,在后面讲解的时候就能看出来了,先定义一个类来实现它:
#@save
class PositionalEncoding(nn.Module):"""位置编码"""def __init__(self, num_hiddens, dropout, max_len=1000):super(PositionalEncoding, self).__init__()self.dropout = nn.Dropout(dropout)# 创建一个足够长的Pself.P = torch.zeros((1, max_len, num_hiddens))X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)self.P[:, :, 0::2] = torch.sin(X)self.P[:, :, 1::2] = torch.cos(X)def forward(self, X):X = X + self.P[:, :X.shape[1], :].to(X.device)return self.dropout(X)
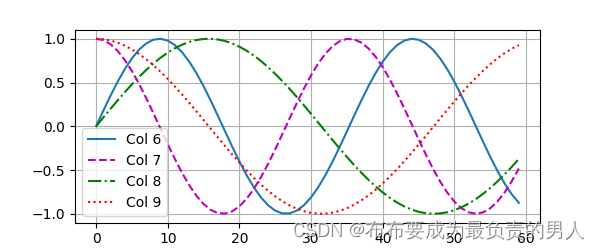
我们可以进行打印图像,可以清晰看到6、7列比8、9列频率高,而6与7(8与9同理)由于正余弦函数的相位交替,而导致偏移量不同。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
d2l.plt.show()
运行结果:
绝对位置信息
其实就是二进制了,想象一下0-7的二进制表示是各不相同的,而且容易知道:较高比特位的交替频率低于较低比特位(而使用三教函数的话输出的是浮点数,显然会更省空间)。
相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移σ,位置i+σ处的位置编码可以线性投影位置i处的位置编码来表示。
用数学来表示:
令 w j = 1 / 1000 0 2 j / d ,对于任何确定的位置偏移 σ : [ c o s ( σ w j ) s i n ( σ w j ) − s i n ( σ w j ) c o s ( σ w j ) ] [ p i , 2 j p i , 2 j + 1 ] = [ c o s ( σ w j ) s i n ( i w j ) + s i n ( σ w j ) c o s ( i w j ) − s i n ( σ w j ) s i n ( i w j ) + c o s ( σ w j ) c o s ( i w j ) ] = [ s i n ( ( i + σ ) w j ) c o s ( ( i + σ ) w j ) ] ——积化和差 = [ p i + σ , 2 j p i + σ , 2 j + 1 ] 令w_j=1/10000^{2j/d},对于任何确定的位置偏移σ:\\ \begin{bmatrix} cos(σw_j)&sin(σw_j)\\ -sin(σw_j)&cos(σw_j) \end{bmatrix} \begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix}\\ =\begin{bmatrix} cos(σw_j)sin(iw_j)+sin(σw_j)cos(iw_j)\\ -sin(σw_j)sin(iw_j)+cos(σw_j)cos(iw_j) \end{bmatrix}\\ =\begin{bmatrix} sin((i+σ)w_j)\\ cos((i+σ)w_j) \end{bmatrix}——积化和差\\ =\begin{bmatrix} p_{i+σ,2j}\\ p_{i+σ,2j+1} \end{bmatrix} 令wj=1/100002j/d,对于任何确定的位置偏移σ:[cos(σwj)−sin(σwj)sin(σwj)cos(σwj)][pi,2jpi,2j+1]=[cos(σwj)sin(iwj)+sin(σwj)cos(iwj)−sin(σwj)sin(iwj)+cos(σwj)cos(iwj)]=[sin((i+σ)wj)cos((i+σ)wj)]——积化和差=[pi+σ,2jpi+σ,2j+1]
2×2投影矩阵不依赖于任何位置的索引i。
小结
1、在自注意力中,查询、键和值都来自同一组输入。
2、卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
3、为了使用序列的顺序信息,可以通过在输入表示中添加位置编码,来注入绝对的或相对的位置信息。