494. 目标和
- 原题链接:
- 完成情况:
- 解题思路:
- 数组回溯法
- 动态规划
- 参考代码:
- 数组回溯法
- __494目标和__动态规划
- 经验吸取
原题链接:
494. 目标和
https://leetcode.cn/problems/target-sum/description/
完成情况:
解题思路:
数组回溯法
backTrack(nums, target, index+1, curSum+nums[index]);
backTrack(nums, target, index+1, curSum-nums[index]);
动态规划
假设P是正子集,N是负子集 例如: 假设nums = [1, 2, 3, 4, 5],target = 3,一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]sum(P) - sum(N) = targetsum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)2 * sum(P) = target + sum(nums)因此,原来的问题已转化为一个求子集的和问题: 找到nums的一个子集 P,使得sum(P) = (target + sum(nums)) / 2,该式已经证明了target + sum(nums)必须是偶数,否则无解求子集的问题可以转化为01背包问题定义二维数组dp,其中dp[i][j]表示在数组下标为0...i的元素中任选元素,使得这些元素之和等于j的方案数


参考代码:
数组回溯法
package 西湖算法题解___中等题;public class __494目标和__数组回溯法 {int res = 0;public int findTargetSumWays(int[] nums, int target) {backTrack(nums,target,0,0);return res;}/**** @param nums 数组* @param target 目标值* @param index 索引位置* @param curSum 当前累计和*/private void backTrack(int[] nums, int target, int index, int curSum) {//1 <= nums.length <= 20//这种方法,属于递归,完全是因为数量级太小了//不然肯定算不出来的。if (index == nums.length){ //所有元素已经遍历完了if (curSum == target){res++;}}else{backTrack(nums, target, index+1, curSum+nums[index]);backTrack(nums, target, index+1, curSum-nums[index]);}}}__494目标和__动态规划
package 西湖算法题解___中等题;public class __494目标和__评论区大佬 {/**题目介绍:就是说有一个数组,然后要在数组任意两两元素间插入一个【+】或者【-】最终要构成target这个值,问你有多少种拼接情况。*/public int findTargetSumWays(int[] nums, int target) {//很明显的一道dp题目,最终结果取决于过程叠加。/**假设P是正子集,N是负子集 例如: 假设nums = [1, 2, 3, 4, 5],target = 3,一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]sum(P) - sum(N) = targetsum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)2 * sum(P) = target + sum(nums)因此,原来的问题已转化为一个求子集的和问题: 找到nums的一个子集 P,使得sum(P) = (target + sum(nums)) / 2,该式已经证明了target + sum(nums)必须是偶数,否则无解求子集的问题可以转化为01背包问题定义二维数组dp,其中dp[i][j]表示在数组下标为0...i的元素中任选元素,使得这些元素之和等于j的方案数*/int nLength = nums.length;//先去掉点特殊情况int sum = 0;for (int num:nums){sum += num;}// target + sum(nums)必须是偶数,否则无解 //要使target = nums[]的加减操作合,则它们必须同奇或者同偶// Math.abs(target) <= sum才有解 //目标值不能比绝对值求和还大//偶数判断还可以用 (lambda & 1) == 1 去判断if (((sum + target) & 1) == 1 || Math.abs(target) > sum){return 0;}int size = (sum + target) / 2;// 定义二维数组dp,其中dp[i][j]表示在数组下标为0...i的元素中任选元素,使得这些元素之和等于j的方案数int dp_findTargetSumWays [][] = new int[nLength][size+1];// 对dp[0][j]的初始化:除dp[0][0]和dp[0][nums[0]]外全部初始化为0// dp[0][0] = 1:nums[0]不为0时,此时dp[0][0]和dp[0][nums[0]]不重合,只有不选nums[0],其总和为0// dp[0][0] = 2:nums[0]为0时,此时dp[0][0]和dp[0][nums[0]]重合,选或者不选nums[0],其总和都为0if (nums[0] <= size){dp_findTargetSumWays[0][nums[0]] = 1;}if (nums[0] == 0){dp_findTargetSumWays[0][0] = 2;}else {dp_findTargetSumWays[0][0] = 1;}// 对dp[i][0]的初始化,可以放在下面整个dp的递推代码中for (int i = 1;i<nLength;i++){if (nums[i] == 0){//当nums[1]为0时,选择或者不选择nums[1]都可以使总和为0,//即dp[i][0] = dp[i - 1][0] + dp[i - 1][0 - nums[i]] = 2 * dp[i -1][0]dp_findTargetSumWays[i][0] = 2*dp_findTargetSumWays[i-1][0];}else{// 当nums[i]不为0时,只有不选nums[i]才可以使总和为0dp_findTargetSumWays[i][0] = dp_findTargetSumWays[i-1][0];}}// dp[i][j]递推:由于初始化时都将i = 0和j = 0的情况已经赋值,所以直接从i = 1和j = 1开始// 完全可以将上面对dp[i][0]的初始化放在此处,只需要将j从0开始for (int i=1;i<nLength;i++){for (int j=1;j<=size;j++){if (j>=nums[i]){dp_findTargetSumWays[i][j] = dp_findTargetSumWays[i-1][j] + dp_findTargetSumWays[i-1][j-nums[i]];}else{dp_findTargetSumWays[i][j] = dp_findTargetSumWays[i-1][j];}}}return dp_findTargetSumWays[nLength-1][size];}
}经验吸取
-
首先,如果最终结果可以由其中的每一步过程,造成影响得来,那么就可以考虑用dp
-
dp的难点就在于状态转移方程!!!如何将一个问题转化很重要!!!
-
转化形式应该为:
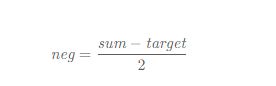
未知状态 = 已知确定目标值

dp数组过程推演情况。







![[UE4][C++]使用qrencode动态生成二维码](https://img-blog.csdnimg.cn/27ad5d40a9364a59aee5f511ca8dbd7e.png)