概念
逻辑回归是一种用于二分分类问题的统计学习方法,尽管名字中带有"回归"一词,但实际上它用于分类任务。逻辑回归的目标是根据输入特征来预测数据点属于某个类别的概率,然后将概率映射到一个离散的类别标签。
逻辑回归模型的核心思想是将线性回归模型的输出通过一个逻辑函数(通常是Sigmoid函数)进行转换,将连续的预测值映射到0和1之间的概率值。这个概率可以被解释为数据点属于正类的概率。
公式说明
逻辑回归的数学表达式如下(假设有 n 个特征):
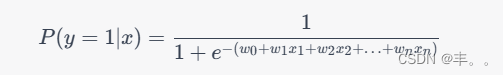
其中, P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x) 是给定输入特征 x x x 后数据点属于正类的概率, w 0 , w 1 , w 2 , … , w n w_0, w_1, w_2, \ldots, w_n w0,w1,w2,…,wn 是模型的权重参数, x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn 是对应的特征值, e e e 是自然常数。
逻辑回归模型可以通过最大似然估计等方法来学习权重参数。一旦模型学习完成,可以使用预测函数来对新的数据点进行分类预测。
代码实现
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 准备示例数据
X, y = ... # 特征矩阵和标签# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建并训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)# 在测试集上进行预测
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")