提前声明，本篇文章是我对我之前B+树那篇文章的追加部分和补充的知识点，建议各位在看本篇文章的时候时已经了解了数据库索引B+树的基本原理，否则有些地方可能理解起来会多一些难度哦！
深入理解索引B+树的基本原理_程序猿ZhangSir的博客-CSDN博客
https://blog.csdn.net/m0_70325779/article/details/132182698?spm=1001.2014.3001.5501
目录
1. 什么是 Hash
1.1 Hash 函数
1.2 Hash 碰撞
1.3 HashMap 的时间复杂度
2. AVL树
2.1 简单了解AVL树
2.2 AVL树的时间复杂度
2.3 AVL树的缺点
3. B 树
4. B+ 树
5. 为什么数据库不采用哈希表存储数据呢？
6. 为什么数据库不采取B树的结构存储数据呢？
7. 自适应 Hash 索引
1. 什么是 Hash
1.1 Hash 函数
Hash 本身其实是一个函数，又被称为散列函数，它可以大幅提高我们对数据的检索效率。因为它是散列的，所以在存储数据的时候，它也是无序的。
Hash 算法是通过某种确定性的算法(例如MD5，SHA1，SHA2，SHA3)将输入转变成输出，相同的输入结果永远会得到相同的输出。
1.2 Hash 碰撞
熟悉Java中 HashMap 的同学应该都知道，我们在往Map集合中存放元素的时候，它会先对要往集合中存放的元素的key值做一个哈希运算，从而确定它要存入的位置。理论上每一个对象都会存放在不同的地方，但当存放的对象越来越多时，有可能后来添加的元素的key值计算得出的结果与之前已经存入的元素的key的哈希值相等，这种现象就被称为哈希碰撞。当产生哈希碰撞的时候，我们会将后添加的元素与之前就已经存在的元素形成一个链表，当再次发生哈希碰撞时，就继续在链表尾部添加即可。
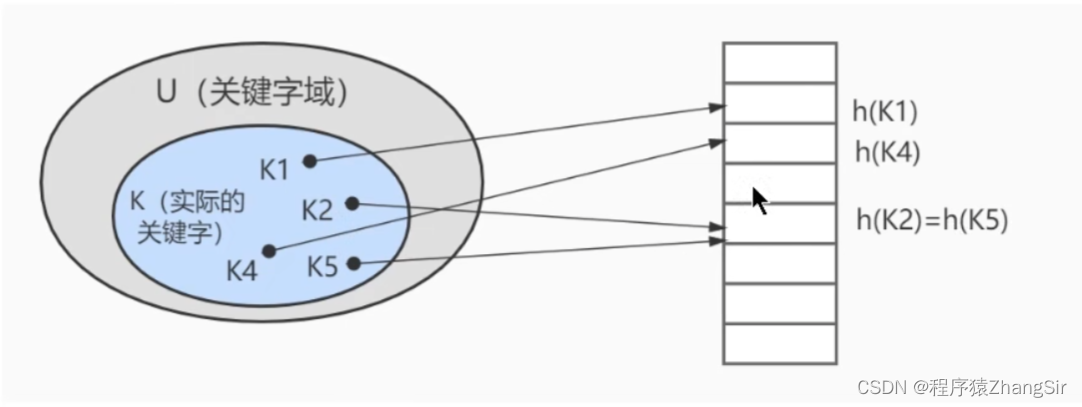
如下图所示，我们也可以采取这种方式将数据库中的数据以哈希的方式存储到哈希表中，可以看到h(k2)与h(k5) 就产生了哈希碰撞。
1.3 HashMap 的时间复杂度
我们知道，HashMap 其实就是一个数组，它是有下标的，我们在 查询/删除/修改 元素的时候，都可以直接通过哈希函数计算出来的哈希值精确到某个元素的位置，这里我们不考虑哈希碰撞形成的链表，因此 HashMap 的查询/删除/修改 元素的时间复杂度都是O(1)，也就是常量级别的，可以说是非常非常快。
2. AVL树
2.1 简单了解AVL树
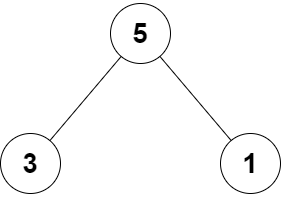
AVL树，其实也叫平衡二叉树，或叫平衡二叉搜索树，它通常满足一个特点，左子节点的值都比父节点小，右子节点的值都比父节点大，如下图所示
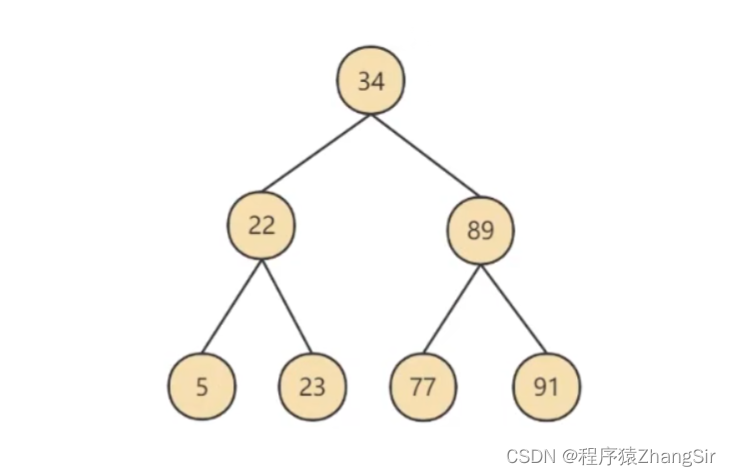
在这种情况下，我们去寻找数据91，只需要查找三次即可得出结果。
2.2 AVL树的时间复杂度
从上面我举得例子不难看出，在AVL树中查找数据时，每查找一次，砍掉一半的数据，再查找一次，再砍掉一半的数据，所以不难看出，AVL树的时间复杂度是 O(log2n)。
2.3 AVL树的缺点
AVL树时间复杂度虽然低，但也存在一些缺点，因为AVL树要保持高度的平衡，所以需要经常性旋转，旋转也是非常耗费时间，并且，随着数据越来越多，AVL树的深度也会越来越大，如下图所示，当数据达到31个的时候，树的高度已经有5层了。我们知道，每多一层，与磁盘就要多进行一次IO操作，非常耗费时间，所以我们就在想，能不能把树的高度降低一些，但同时又能存足量的元素呢？这就有了下面要说M叉树，也可以理解为B树。
3. B 树
经过了上面对AVL树的分析，我们也知道了，当树的叉越多时，存储的数据也越多，与磁盘交互的次数也越少，我们把上方的二叉树转换成三叉树，当然也可以转换成四叉树，五叉树都是可以的，这里我就以三叉树为例。
这个时候，我们还是能存储31个元素，并且树的高度由原来的5层降低到了4层，提高了我们数据的查找效率，这就是我们索引的雏形，我们就可以将数据库中的数据存储在树中，得到如下简易模型
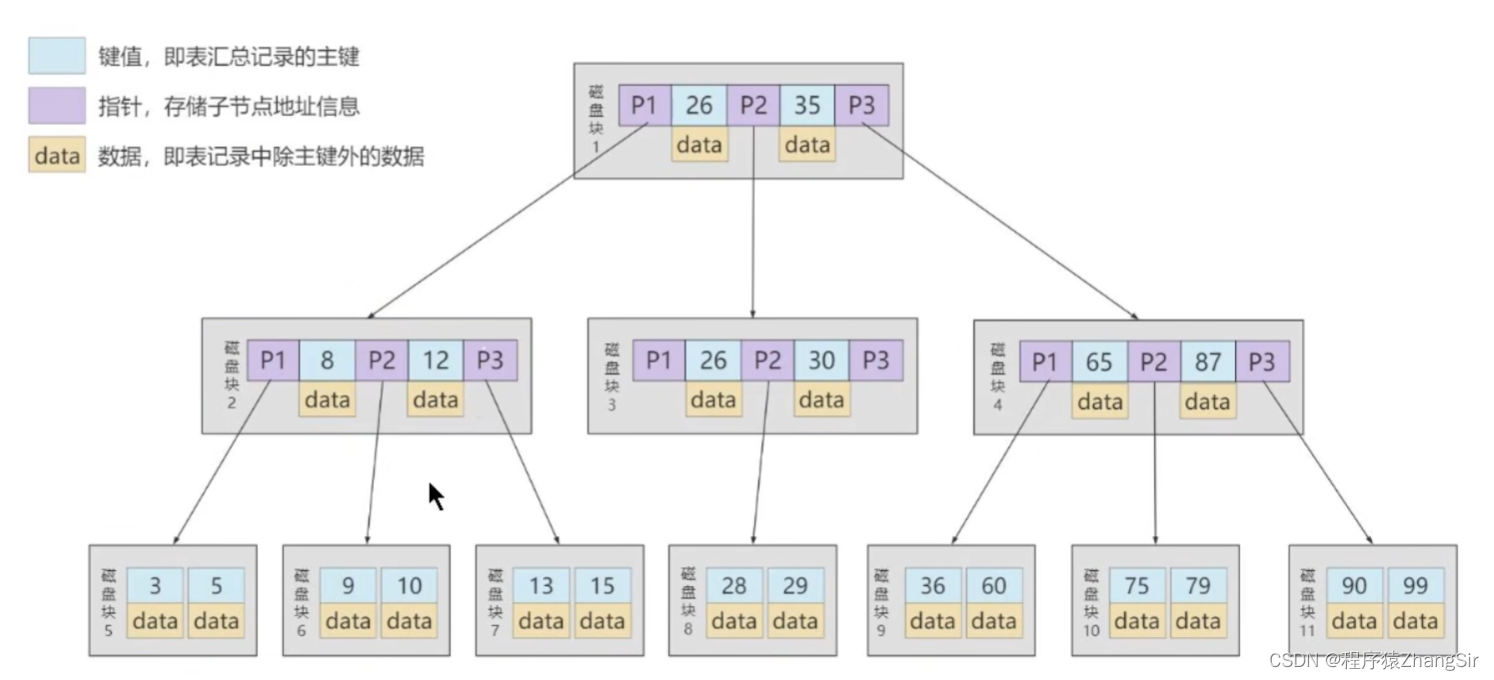
上图中就是索引最开始形成的B树结构图，左上角也有标注，这个时候我们可以看到，在原始B树中，磁盘块1234这几个非根节点中还存放着数据呢，P1是地址值指向磁盘块2，并且里面记录的主键值都是小于26的；P3是地址值指向磁盘块4，里面记录的数据主键值都是大于35的；P2是地址值指向磁盘块3，里面记录的数据主键值都是在26与35之间的。下方的磁盘块2，3，4中都是同理，依次往下类推。
这种数据的存储方式和查找方式性能已经非常优秀了，但是还有一个缺点，我们将原来的2叉树转变成M多叉树，目的就是为了存储更多的数据，但大家看，在磁盘块2，3，4中，P1，P2，P3都是指针，不会占用多少空间，但8和12的data存储的是真实的数据，会占用部分磁盘空间，而且这个时候还有分成了三段，如果分的段更多，也会存储更多的数据，这就会导致我们无法存储更多的指针数据，违背了我们的初衷。于是，我们就可以对这个B树做进一步的升级(当然也不只是因为这一个原因，后面我们还会说到，这里先说这一点就)演化成了我们现在的 B+ 树结构。
4. B+ 树
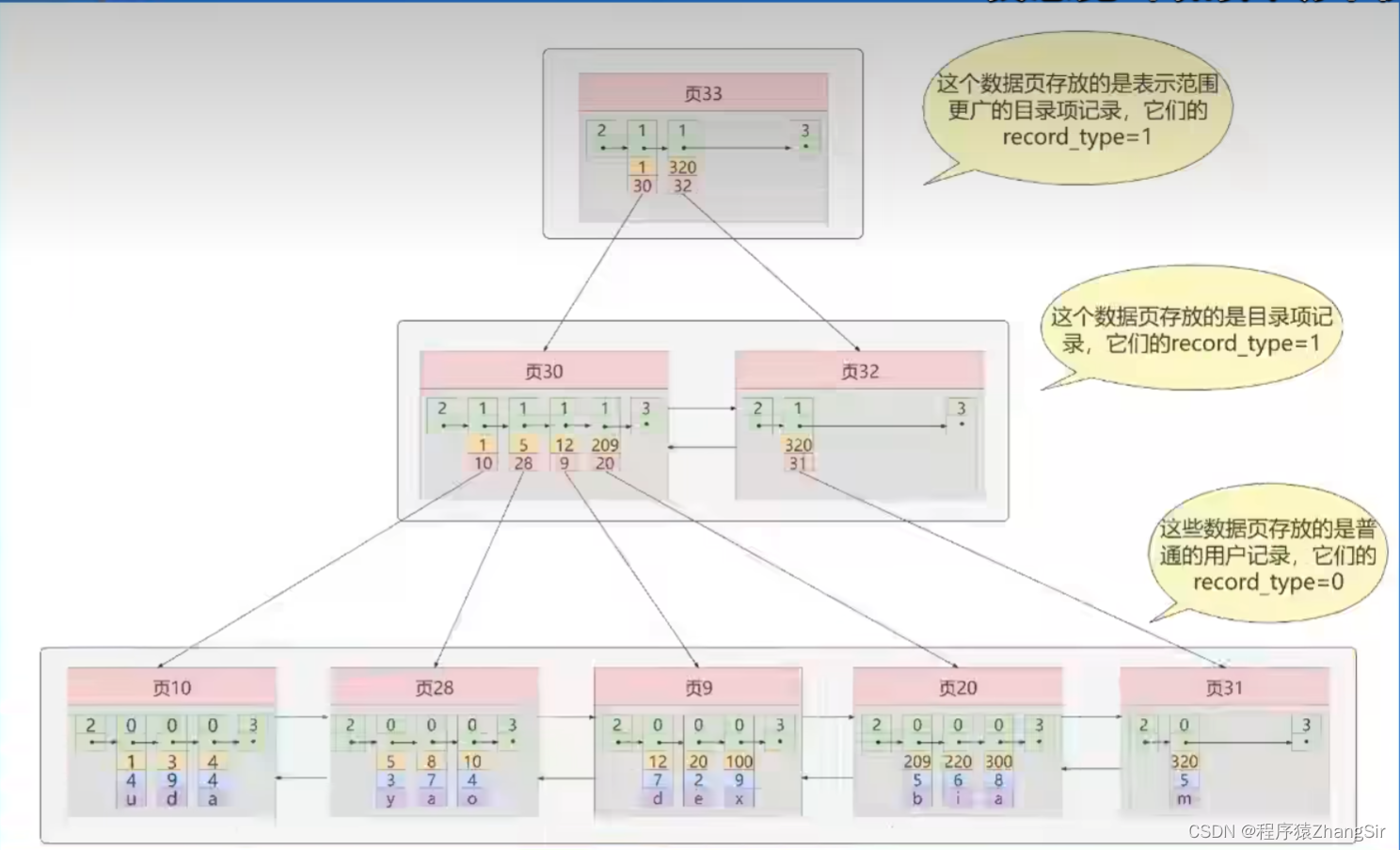
如上图所示，就是从B树演化形成的 B+ 树，在 B+ 书中，我们舍弃了B书中非叶子节点也存储真实数据做法，将所有的真实数据全部存放在叶子节点中，这样我们的目录页就可以存放更多的指针数据。并在每一页都会添加一个数组，数组中记录着该页中的所有元素并按照从小到大的顺序排列。
例如上图，顶层目录页33记录了数据1，320，下方对应着页30与页33的地址值；中间目录页30中存储着 1，5，12，209，数据下方各自对应着该页的地址值；当我们想要查找（100，9，x）这条数据时，做判断，发现（100，9，x）的相关信息应存储在中间页30中，在进入中间页30寻找，经过判断发现该数据存放在页9中，根据对应的地址值找到页9，然后在页9中就可以获取到数据（100，9，x）了，不管查询那个数据，都是这样的一个过程，查询速度非常稳定，并且中间目录页不存储真实数据只存储地址值，可以存储更多的叶子节点页数据。
5. 为什么数据库不采用哈希表存储数据呢？
这其实是一个面试题，刚才我们也分析过了，哈希表的时间复杂度为O(1)，常量级别，是最快的，那么数据库存储数据时为什么不采用哈希表的形式存储呢？原因有以下几点：
（1）范围查找显得无力
如果我们采用哈希表的结构存储，你会发现，它只能满足我们对精准值得查找，当我们在数据库中加入了BETWEEN...AND...或IN这些范围查找关键字的时候，哈希表就没有优势了，而且哈希表还是乱序的，这就导致我们在进行范围查找时，时间复杂度为会从O(1)退化成O(n)，而我们的树形结构时间复杂度稳定在O(log2n)，这个时候我们就会发现，哈希表就没有优势了。
（2）排序浪费时间
因为哈希表是乱序存储，当我们需要进行ORDER BY 的时候，每次ORDER BY底层都要排一次序，而我们的树形结构在存储是就是有序的，不管什么时候取数据都省去了排序的时间。我们存储。
（3）不太支持联合索引
我们知道，B+树中是支持联合索引的，并会对多因进行排序，如果我们使用哈希表存储数据，当我们将字段C1与字段C2联合作为主键时，哈希存储就会把C1和C2作为一个整体计算哈希值，不会单个做哈希值计算。这样就乱套了，因为两个不一样的字段加在一起哈希值是可能相同的。
（4）索引列重复时效率低
我们知道计算哈希值就是为了避免哈希碰撞，如果一些字段肯定会出现碰撞，例如性别，年龄这些字段，那么哈希碰撞的概率就会非常大，它会遍历哈希桶中的每一个元素作比较，非常耗时，所以哈希索引通常不会用在容易出现重复的字段上。
6. 为什么数据库不采取B树的结构存储数据呢？
通过上面我对B树结构的分析，我们可以得出结论，B树中数据不仅存储在叶子节点中，在非叶子节点也存储着数据，那么为什么数据库要采用B+树存储数据而不采用B书呢？它们两个才存储数据时有哪些区别？这也是一道经典面试题。我总结了一下几点原因：
（1）B树中非叶子节点存储数据，会导致非叶子节点可存储的叶子节点数量表少，间接导致存储的数据量也随之变少；
（2）当我们对数据进行修改操作时，若是修改的叶子节点无可厚非，若是修改的数据在非叶子节点中，就会导致非叶子节点可能会发生移动，非常消耗时间和性能；而如果我们使用的是B+树，则发生的概率会很小，我们几乎只需要更改也增加节点中的数据即可，效率会更高一些；
（3）相比于B+树，B树的查找效率不够稳定，B+树几乎可能稳定在三次查找内必查找到数据，而B树却显得不那么稳定。
7. 自适应 Hash 索引
在 InnoDB 引擎中，虽然本身不支持哈希索引，但是它提供了一个自适应的哈希索引，这个是默认开启的，当我们经常性地对数据库中的同一些数据做查询操作时，它就会将这些数据存放到哈希表中，以便我们以后更加快速的查找。
经过自适应哈希索引优化之后，之前我们需要进行一层层目录的查找，但是哈希表就可以让我们一步到位，省去检索的时间。
