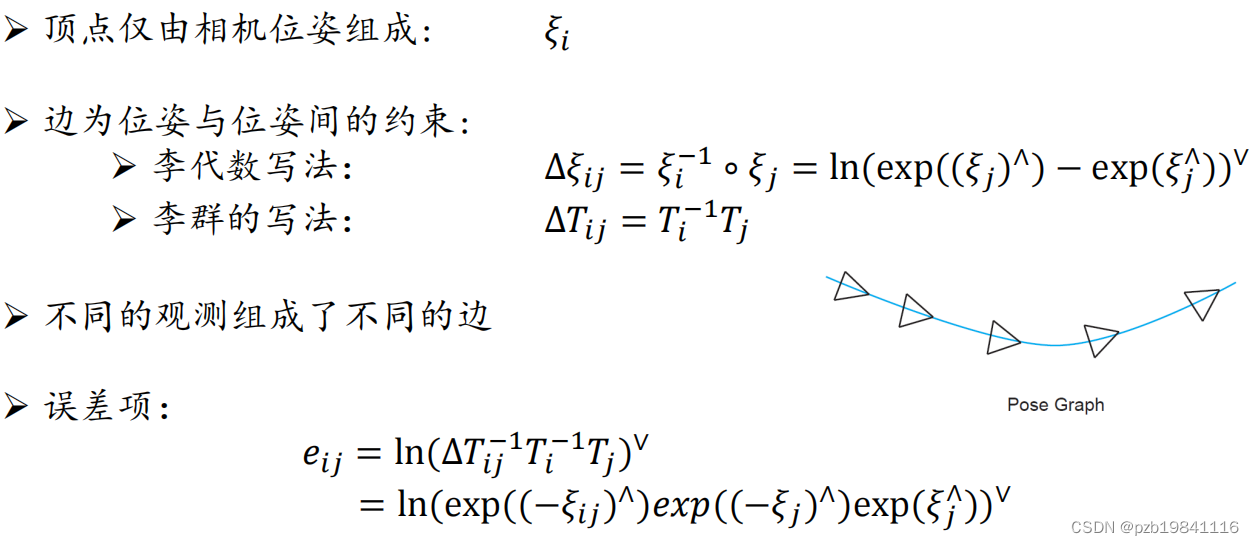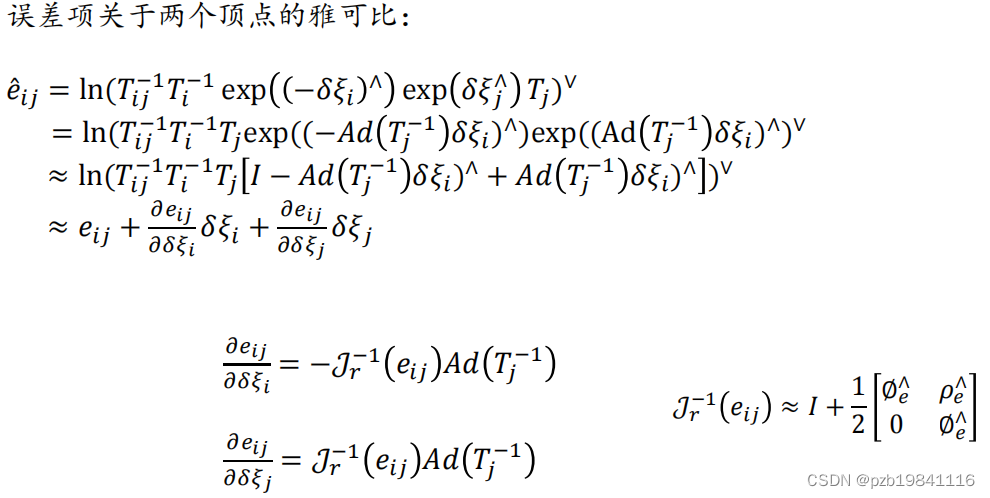在七月算法报的班,老师讲的蛮好。好记性不如烂笔头,关键内容还是记录一下吧,课程入口,感兴趣的同学可以学习一下。
-------------------------------------------------------------------------------------------------------------------------------
后端的目标:从带噪声的数据估计内在状态——状态估计问题。主流方法分为两大类:
❑ 渐进式(Incremental/Recursive)
❑ 批量式(Batch)
其中,渐进式(Incremental/Recursive)的思想和主流方法如下:
➢ 保持当前状态的估计,在加入新信息时,更新已有的估计(滤波)
➢ 线性系统+高斯噪声=卡尔曼滤波器
➢ 非线性系统+高斯噪声+线性近似=扩展卡尔曼
➢ 非线性系统+非高斯噪声+非参数化=粒子滤波器
➢ Sliding window filter & multiple state Kalman(MSCKF)
批量式(Batch)的思路为:
➢ 给定一定规模的数据,计算该数据下的最优估计(优化)
渐进式的作用是根据观测的结果,修正自己对位姿的估计。没有观测,则随着机器人的移动,自身的位姿误差会越来越大。
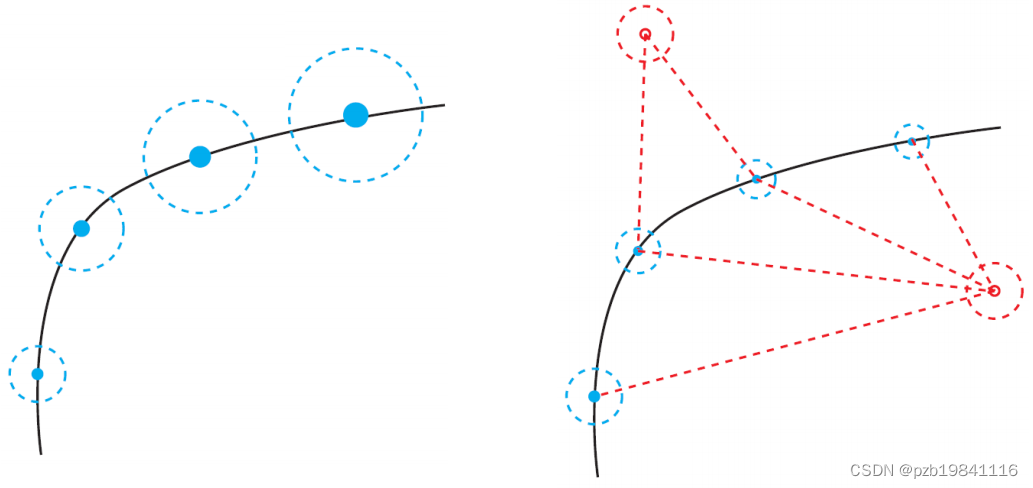
与之前保持一致,xk表示位姿,zk表示观测
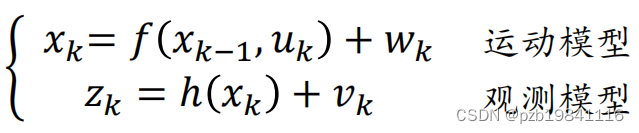
则k时刻的位姿,与原始位姿、运动序列和观测序列有关


这其中涉及到当前时刻与之前各时刻位姿之间的关系,一般分为两种:
➢ 假设𝑘时刻状态只和𝑘-1时刻有关
➢ 假设𝑘时刻状态与先前所有时刻均相关
常用第一种,也叫作马尔科夫性。
.
其中,卡尔曼滤波用在线性模型、高斯噪声的情况之下
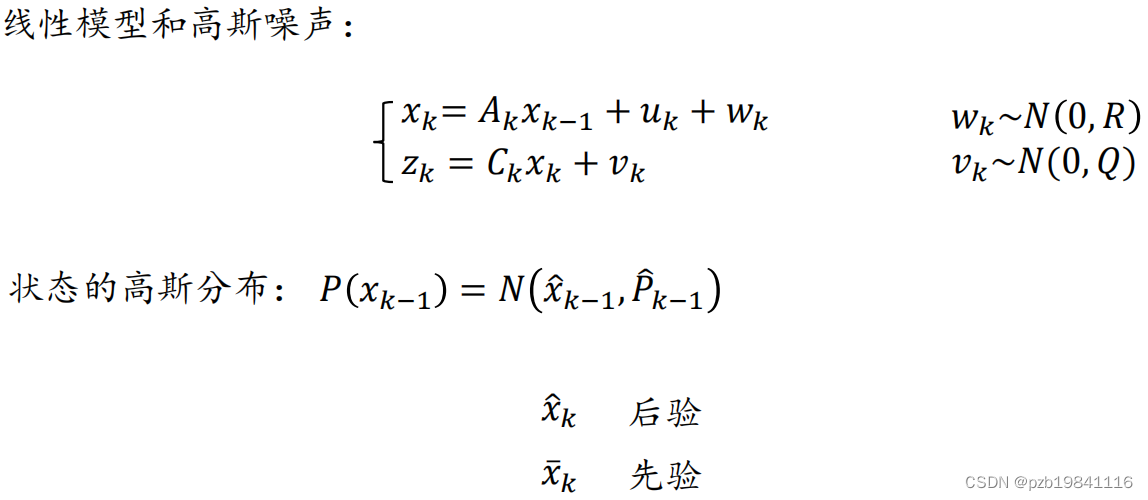
高斯分布的线性变换,仍然属于高斯分布。
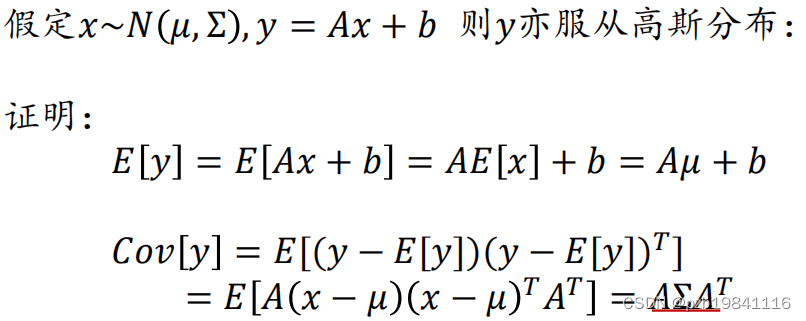
计算过程很复杂,最后只要记住这几个公式即可。
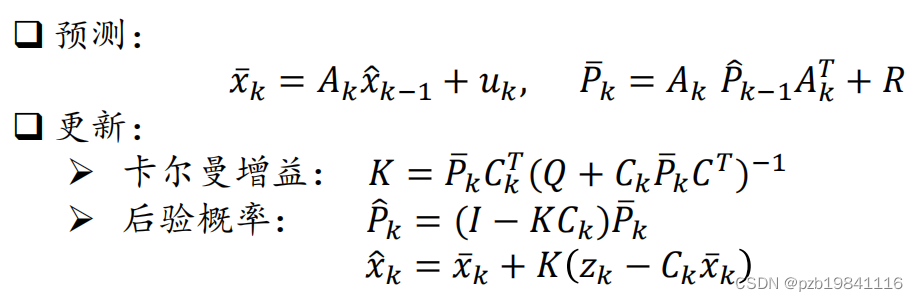
当运动函数与观测函数为非线性函数时,用一阶Taylor展开

分析的工具为扩展卡尔曼滤波
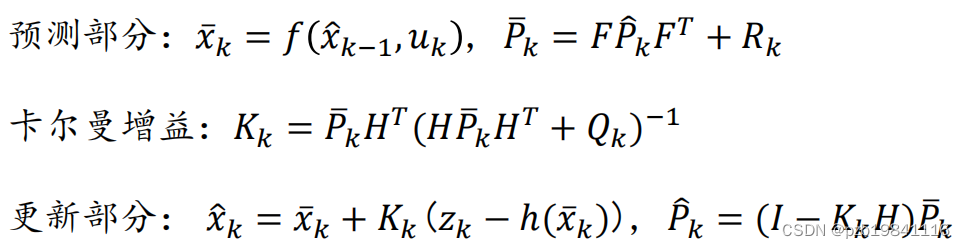
扩展卡尔曼滤波的优缺点
❑ Advantage
➢ 推导简单清楚,适用各种传感器形式
➢ 易于做多传感器融合
❑ Disadvantage
➢ 一阶马尔可夫性过于简单
➢ 可能会发散(要求数据不能有 outlier)
➢ 线性化误差
➢ 需要存储所有状态量的均值和方差,平方增长
批量法的思路

Bundle Adjustment问题与图结构的关系:
➢ BA虽然是个纯优化问题,但亦可以用图模型清晰地表述出来
➢ 顶点为优化变量,边为运动/观测约束
➢ 本身还有一些特殊的结构
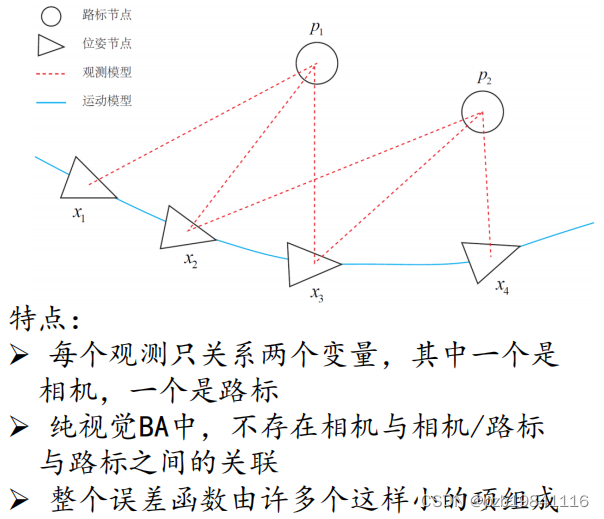
BA使用高斯-牛顿或者L-M算法计算

这里的雅可比矩阵为一个稀疏阵。
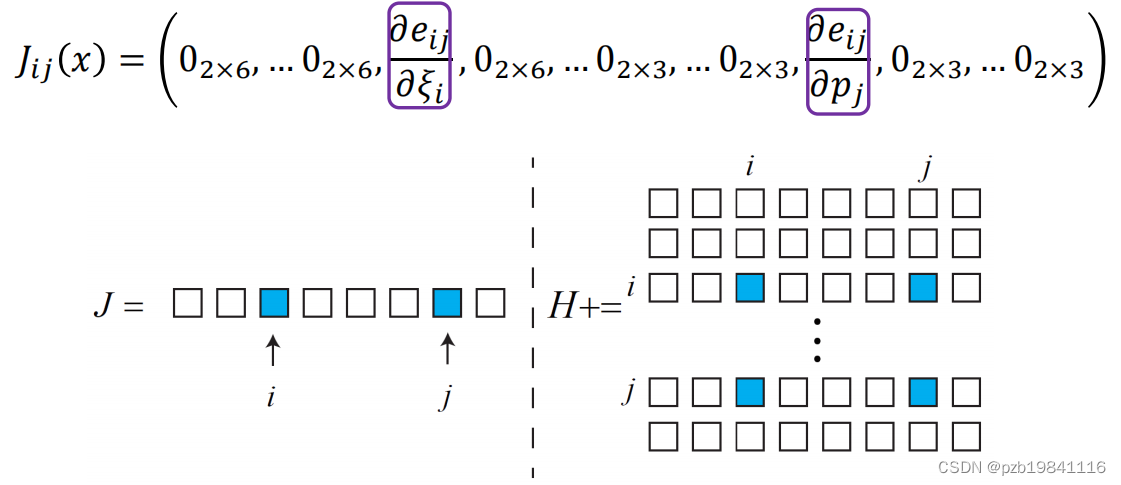
目标函数与雅可比矩阵的情况

雅可比矩阵与H矩阵的稀疏性特点
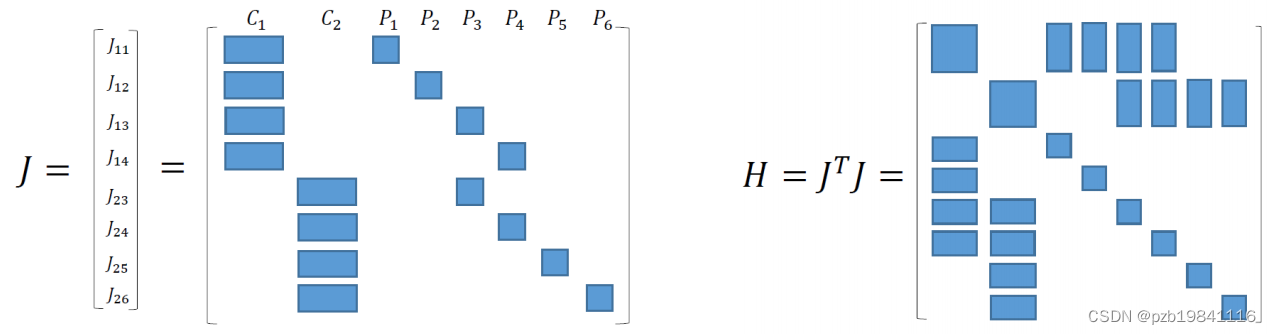
图模型结构与H矩阵之间的映射关系
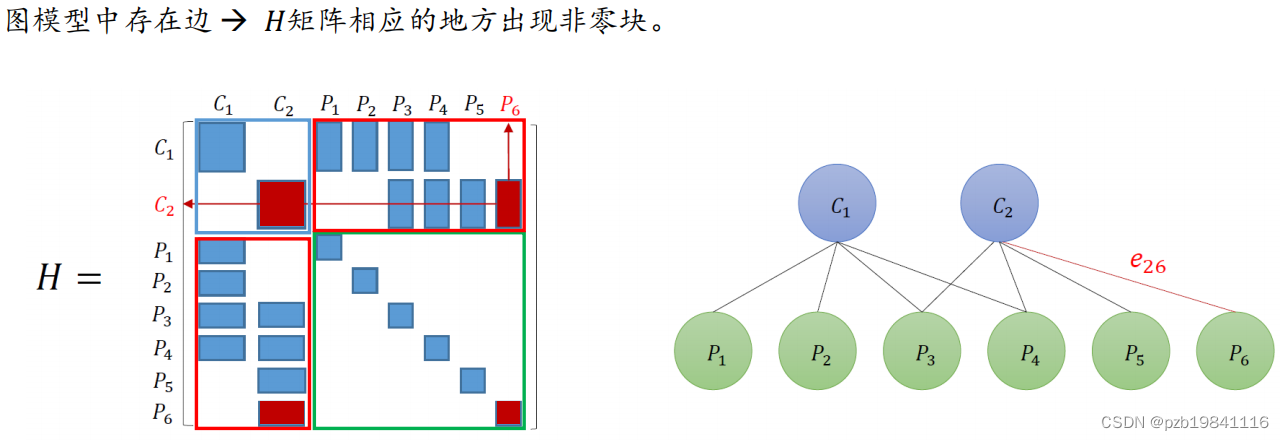
利用H矩阵的特点,可以加速计算过程。


迭代法与批量发之间的区别
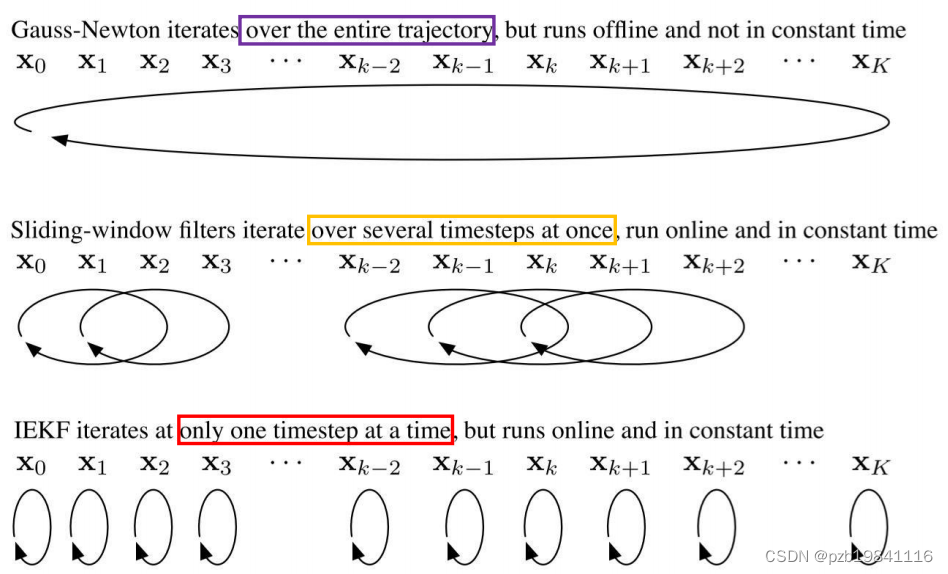
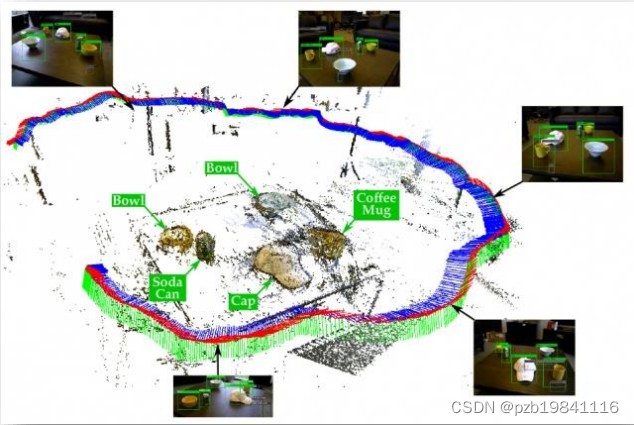
在SLAM中使用Bundle Adjustment,用来做关键帧和地图的管理
批量方法:
➢ 用BA优化一部分图
➢ 其余的固定
递归方法:
➢ 保留一定数量的关键帧
➢ 使用BA来优化窗口内的关键帧
➢ 新的关键帧到来时,边缘化老的关键帧
位姿图与BA之间的关系
实际当中Bundle Adjustment的计算量很大:
➢ 通常放在单独的后台线程中计算而无法实时
➢ 主要计算来自于大量的特征点
Pose Graph 即是省略了特征点的 Bundle Adjustment。
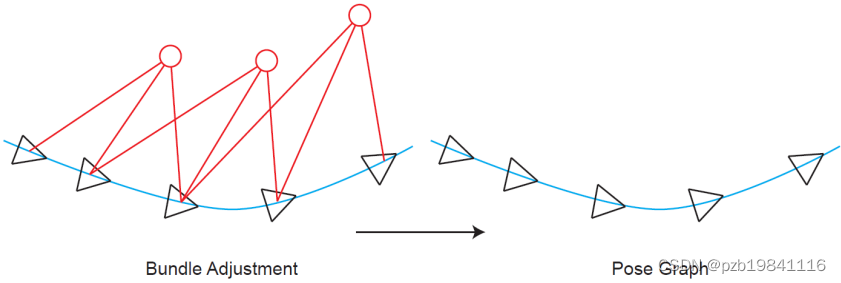
位姿图的计算过程