因果推断(五)基于谷歌框架Causal Impact的因果推断
除了传统的因果推断外,还有一些机器学习框架可以使用,本文介绍来自谷歌框架的Causal Impact。该方法基于合成控制法的原理,利用多个对照组数据来构建贝叶斯结构时间序列模型,并调整对照组和实验组之间的大小差异后构建综合时间序列基线,最终预测反事实结果。
CausalImpact适用于时间序列在干预后的效果评估,例如某功能上线后是否提升了用户活跃。本文参考自CausalImpact 贝叶斯结构时间序列模型、tfcausalimpact官网示例。
准备数据
# pip install tfcausalimpact
import tensorflow as tf
from causalimpact import CausalImpact
import pandas as pdtf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR) # 忽略tf警告信息
以下数据如果有需要的同学可关注公众号HsuHeinrich,回复【因果推断05】自动获取~
# 读取数据
data = pd.read_csv('arma_data.csv')
data.iloc[70:, 0] += 5 # 手动增加y值。构造提升效果
data.head()
数据格式:
第一列为因变量,后面为协变量,例如本立中的y和X。
数据需要标准化处理,可参考官方示例
# causalimpact.misc.standardize标准化 import numpy as np import pandas as pd import pytest import tensorflow as tf import tensorflow_probability as tfp from numpy.testing import assert_array_equal from pandas.util.testing import assert_frame_equalfrom causalimpact import CausalImpact from causalimpact.misc import standardizedata = pd.read_csv('tests/fixtures/btc.csv', parse_dates=True, index_col='Date') training_start = "2020-12-01" training_end = "2021-02-05" treatment_start = "2021-02-08" treatment_end = "2021-02-09" pre_period = [training_start, training_end] post_period = [treatment_start, treatment_end]pre_data = rand_data.loc[pre_int_period[0]: pre_int_period[1], :] # 标准化 normed_pre_data, (mu, sig) = standardize(pre_data)# 自定义标准化 x-mu/sigma normed_my_data = (pre_data - mu) / sig # 伪代码 # 定义model_args参数 model_args == {'fit_method': 'hmc', 'niter': 1000, 'prior_level_sd': 0.01, 'season_duration': 1, 'nseasons': 1, 'standardize': True}
| y | X | |
|---|---|---|
| 0 | 118.188694 | 99.795292 |
| 1 | 120.233276 | 100.663180 |
| 2 | 118.627775 | 98.883699 |
| 3 | 119.609722 | 100.448941 |
| 4 | 121.391508 | 101.561734 |
模型拟合
# 分析报告
pre_period = [0, 69] # 干预前时期
post_period = [70, 99] # 干预后时期ci = CausalImpact(data, pre_period, post_period)
print(ci.summary())
ci.plot()
Posterior Inference {Causal Impact}Average Cumulative
Actual 125.23 3756.86
Prediction (s.d.) 120.23 (0.33) 3606.76 (9.97)
95% CI [119.58, 120.89] [3587.5, 3626.57]Absolute effect (s.d.) 5.0 (0.33) 150.11 (9.97)
95% CI [4.34, 5.65] [130.3, 169.36]Relative effect (s.d.) 4.16% (0.28%) 4.16% (0.28%)
95% CI [3.61%, 4.7%] [3.61%, 4.7%]Posterior tail-area probability p: 0.0
Posterior prob. of a causal effect: 100.0%For more details run the command: print(impact.summary('report'))
- Causal Impact报告
- 实验最终的平均预测值(prediction)为120.34,平均实际值(actual)为125.23;而累计预测值3610.16,累计实际值3756.86;这里的平均数据范围就是上述虚线之后(干预后)的时间段
- 经过MCMC估计指标绝对效应(absolute effect)平均增长4.89,累计增长146.71;相对比率(relative effect)平均增长4.06%,累计增长4.06%
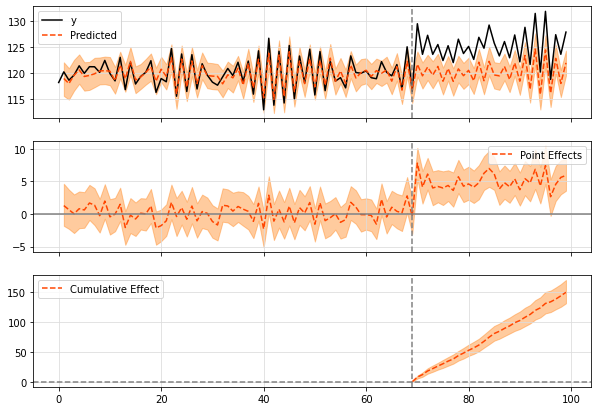
- Causal Impact图
- 第一张图(original)黑色实线为干预前后的实际结果,橙色虚线为模拟的策略未上线时的结果。阴影为置信区间
- 第二张图(pointwise)橙色虚线为策略前后y的差值,可以看到策略上线后,y差值是显著为正的。
- 第三张图(cumulative)橙色虚线为策略上线后的累加值,是持续增大的,可见策略有明显的正向作用。
# 打印详细报告
print(ci.summary(output='report'))

-
也可以用时间序列+多元变量
数据格式:
- 第一列为因变量,后面为协变量,例如本立中的CHANGED和[NOT_CHANGED_1、NOT_CHANGED_2、NOT_CHANGED_3]
- 数据需要标准化处理,同上
# 读取数据
data = pd.read_csv('comparison_data.csv', index_col=['DATE'])
data.head()
| CHANGED | NOT_CHANGED_1 | NOT_CHANGED_2 | NOT_CHANGED_3 | |
|---|---|---|---|---|
| DATE | ||||
| 2019-04-16 | 83836.5 | 85642.5 | 86137.5 | 81241.5 |
| 2019-04-17 | 83887.5 | 86326.5 | 85036.5 | 80877.0 |
| 2019-04-18 | 82662.0 | 87456.0 | 84409.5 | 80910.0 |
| 2019-04-19 | 83271.0 | 89551.5 | 87568.5 | 82150.5 |
| 2019-04-20 | 84210.0 | 90256.5 | 86602.5 | 83083.5 |
pre_period = ['2019-04-16', '2019-07-14']
post_period = ['2019-7-15', '2019-08-01']ci = CausalImpact(data, pre_period, post_period, model_args={'fit_method': 'hmc'}) # model_args参数提高精度,牺牲效率
print(ci.summary())
ci.plot()
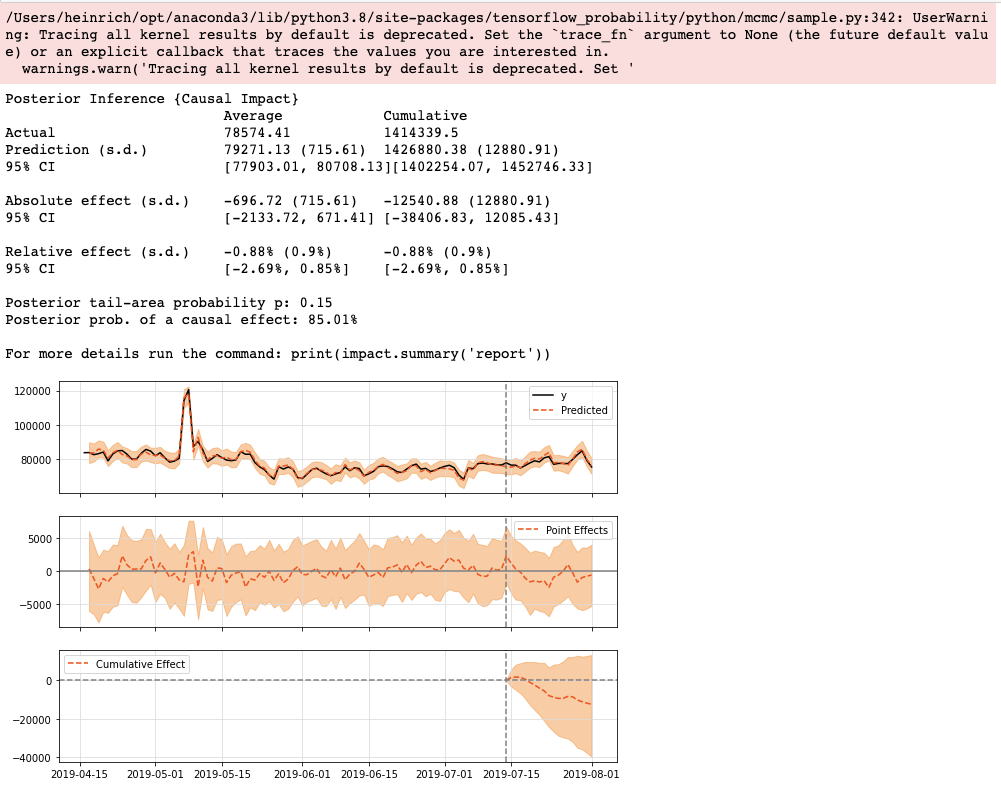
# 打印详细报告
print(ci.summary(output='report'))

总结
这里的分享较为浅显,就当是一种冷门数据分析方法的科普吧,如果想深入了解的同学可自行查找资源进行充电~
共勉~