摘要

近年来，围绕图卷积网络（GCN）这一主题出现了大量的文献。如何有效地利用复杂图中丰富的结构信息（例如具有heterogeneous types of entities and relations(异构实体和关系类型) 的知识图谱）是该领域的主要公开挑战。
大多数GCN方法要么局限于同质边类型（Homogeneous type of edges）（例如，仅引用链接），要么只关注节点的表示学习，而不是 联合传播和更新节点和边的嵌入以实现目标驱动目标 。

本文通过提出一个新的框架来解决这些局限性，即基于知识嵌入的图卷积网络（KE-GCN），它结合了GCN在基于图的信念传播中的强大功能和先进的知识嵌入（又称知识图嵌入）方法的优势，并且超越了它们。

我们的理论分析表明，KE-GCN以图卷积的新视角，将几种著名的GCN方法作为特例进行了简单的统一。在基准数据集上的实验结果表明，在知识图对齐和实体分类任务中，KE-GCN的性能优于强基线方法

“heterogeneous types of entities and relations”（异构实体和关系类型）指的是图谱中存在多种不同类型的实体和关系。异构实体类型指的是图谱中不同种类的实体，可以是人、地点、组织、概念等。每个实体类型具有自己的属性和特征，例如人物的姓名、年龄、职业等。异构关系类型表示图谱中不同实体之间的关系或连接方式。关系类型描述了实体之间的语义关联，例如人物之间的亲属关系、地点之间的空间关系、概念之间的层次关系等。

“Homogeneous type of edges”（同质边类型）
指的是在一个图结构或网络中，存在相同类型的边连接着节点之间。
在图论和网络分析中，图可以由节点（顶点）和边组成。节点表示图中的实体，而边表示节点之间的关系或连接。同质边类型意味着图中的边属于相同的类别或类型，具有相同的属性和语义含义。
举个例子，考虑一个社交网络图，其中节点表示用户，边表示用户之间的关注关系。如果所有的边都代表用户之间的关注关系，那么这些边就属于同质边类型。它们具有相同的属性和意义，即表示用户之间的关注连接。

“Citation links only”（仅引用链接）
指的是在图谱中的某个实体或节点上，仅提供了对其他实体或节点的引用链接，而没有提供这些实体的具体信息或属性。KG的每个实体通常具有一系列的属性和特征，以描述其详细信息。
当一个实体或节点在知识图谱中仅以引用链接的形式出现时，意味着该节点没有直接提供相关实体的具体信息，而是通过引用链接将其与其他实体关联起来。这些引用链接可以指向其他实体的节点或外部资源，例如文献、网页或其他知识库。
"Citation links only"的存在可以有多种原因。其中一种可能是为了简化图谱的规模和复杂性，将某些实体的详细信息存储在其他资源中，而在图谱中只提供对这些资源的引用链接。这样可以减少图谱的存储空间和复杂性，并使得图谱更加灵活和可扩展。

“Jointly propagating and updating the embeddings of both nodes and edges for target-driven objectives”（联合传播和更新节点和边的嵌入以实现目标驱动目标）
是指在图嵌入学习中，同时传播和更新节点和边的表示向量（嵌入），以实现特定的目标任务或目标驱动的学习。目标是将图中的节点和边映射到一个低维向量空间中，以捕捉节点和边之间的语义关系和结构特征。
"Jointly propagating and updating the embeddings of both nodes and edges"意味着在学习过程中，同时对节点和边的嵌入进行传播和更新。传播是指将嵌入向量从一个节点或边传递到其相邻节点或边，以在整个图中传播和聚合信息。更新是指根据目标任务的误差或优化目标，通过梯度下降等方法更新嵌入向量的值。
"Target-driven objectives"表示学习目标或任务的驱动。这些目标可以是不同的，比如节点分类、边预测、图聚类等。通过联合传播和更新节点和边的嵌入，可以在学习过程中同时优化节点和边的表示，以最大程度地利用节点和边之间的关系和结构信息，以实现特定的目标任务。
这种联合传播和更新的方法能够更全面地捕捉图的结构和语义信息，并在目标驱动的学习中提供更好的性能。通过同时考虑节点和边的嵌入，可以更好地建模复杂的图关系和任务要求。
因此，"jointly propagating and updating the embeddings of both nodes and edges for target-driven objectives"指的是在图嵌入学习中，同时传播和更新节点和边的表示向量，以实现特定的目标任务或目标驱动的学习。这种方法可以更好地利用图的结构和语义信息，提供更好的性能和表达能力。

介绍

在最近的机器学习研究中，图卷积网络（GCNs）由于其强大的 基于图的节点特征归纳和信念传播 方法而受到越来越多的关注，并已成功应用于许多现实世界的问题，包括自然语言处理、计算机视觉、推荐系统、流行病学预测等。

现有的GCN有相同的核心思想，即使用图来识别每个节点的邻域，并通过邻域嵌入的递归聚合来学习该节点的嵌入（向量表示）。换言之，图卷积在平滑基于在整个图上的置信传播的节点的学习表示（潜在向量）方面发挥着核心作用。然而，GCN的早期工作也有一个限制因素，即图卷积只用于学习固定边条件下的节点嵌入，而不是联合学习节点和边的最佳嵌入。后来的工作与节点嵌入的学习平行地朝着学习输入图中边的权重的方向发展，它比早期的GCN更强大，更能适应下游任务的模型。然而，这些GCN有一个共同的约束，即输入图中的边必须是同源的，例如引用图中的链接或共生计数矩阵中的元素。这种约束（或假设）极大地限制了GCN在广泛的现实世界应用中的适用性，在这些应用中，对异构关系（边）建模的能力对于基于图的层次和推理的真正效用至关重要。鉴于异构类型的关系在知识库中承载着丰富的语义信息，缺少边缘嵌入的能力从根本上限制了大多数GCN的表达能力和预测能力。

“Graph-based node feature induction and belief propagation”（基于图的节点特征归纳和信念传播）是指在图结构中利用节点特征归纳和信念传播的方法来推断节点的特征表示。
首先，"graph-based node feature induction"是指利用图结构的信息来推断或生成节点的特征表示。这可以通过考虑节点之间的连接关系、邻居节点的特征等方式来实现，以生成更丰富和具有语义信息的节点特征表示。
其次，"belief propagation"是一种在图上进行信息传播和推理的方法。它基于图模型中的概率推理技术，通过迭代地传播节点之间的信念或概率信息来更新节点的状态。在每次迭代中，节点会根据其邻居节点的信息进行更新，并将更新后的信息传播给其他邻居节点。
因此，"graph-based node feature induction and belief propagation"结合了两种方法。它利用图结构的信息进行节点特征归纳，生成丰富的节点特征表示，并使用信念传播的方式在图上进行信息传播和推理。通过这种结合，可以在推断节点特征的过程中充分利用图的拓扑结构和节点之间的关系，从而获得更准确和全面的节点特征表示。这对于图分析、节点分类、关系预测等任务具有重要意义。

递归聚合（Recursive Aggregation）
是指通过迭代地聚合节点的邻居信息来更新节点的表示。
递归聚合的过程通常由多个GCN层组成，每一层都会更新节点的表示。在每一层中，节点会聚合其邻居节点的特征，并结合自身的特征进行更新。这个过程可以迭代多次，以便节点能够获取更多的上下文信息和全局结构。
具体而言，递归聚合的步骤如下：
1.初始化：为每个节点分配初始的特征向量。
2.聚合：对于每个节点，将其邻居节点的特征进行聚合。这通常涉及到对3.邻居节点特征的加权平均或拼接操作。
4.更新：将聚合得到的特征与节点自身的特征进行结合，得到更新后的节点表示。这可以通过使用神经网络层（如全连接层）来实现。
5.重复：重复进行聚合和更新的步骤，直到达到预定的层数或收敛条件。

作为一个间接相关的领域，知识图谱的完善方法（也称为知识图嵌入）近年来得到了深入的研究。针对基于观察到的三元组预测未知关系实体三元组的任务，已经开发了各种算法来联合优化实体和关系的嵌入。再现方法包括TransE、DistMult、ComplEx、RotatE、QuatE等。

KG完善方法与GCN的主要区别在于，前者在表示学习过程中没有明确利用图卷积的信念传播能力；相反，实体-关系-实体三元组在其目标函数中被独立处理。换句话说，那些方法缺乏使用图形的能力在实体和关系的嵌入空间中增强局部平滑性的结构。

“belief propagation power”（信念传播能力）
是指一个节点在信念传播算法中传播其信念或信息的能力。
信念传播是一种在图结构中进行信息传播和推理的方法，它基于图模型中的概率推理技术。在信念传播算法中，节点之间通过传递消息来更新彼此的信念或概率分布。节点根据其邻居节点的信息，特别是传播到它的消息，来更新自身的概率分布。
"Belief propagation power"衡量了一个节点在信念传播过程中对其他节点的影响程度。一个具有较高信念传播能力的节点能够有效地传播其信息给周围的节点，并对整个图的状态产生较大的影响。
通常，信念传播能力与节点的度数（即与其相连的边的数量）和传播的消息的质量有关。具有更多邻居和更准确、有用的消息的节点往往具有更高的信念传播能力。

如何联合利用GCN模型和KG完善方法的优势，对两个实体和关系进行面向任务的表示学习，是一个公开的研究挑战，这方面的代表性工作，或迄今为止我们所知的唯一此类方法是VR-GCN、TransGCN和CompGCN，使用图神经网络来联合学习实体和关系的多层潜在表示（嵌入）。
具体来说，实体嵌入过程递归地聚合了邻域实体表示和关系表示，这是有意义的；然而，学习过程中的关系嵌入部分将实体表示排除在外，这是这些模型的根本限制。

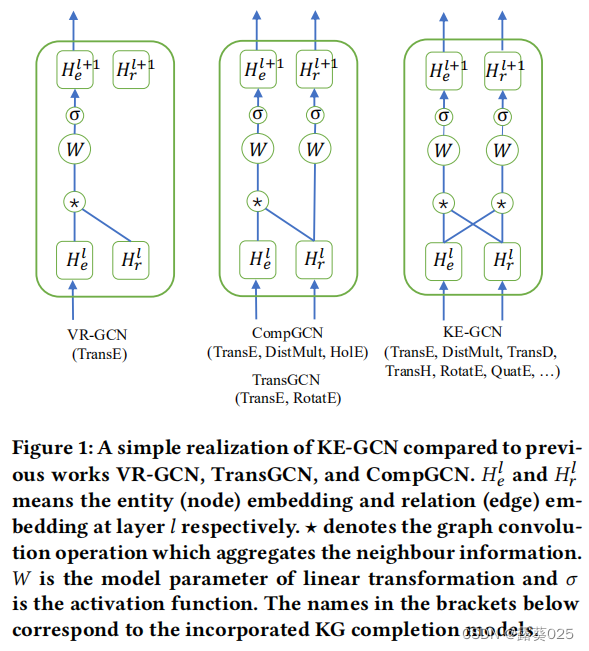
在这里插入图片描述
为了解决上述公开的挑战和现有方法的限制，我们提出了一个新的框架，即KE-GCN（基于知识嵌入的图卷积网络）。它对现有的GCN模型进行了理论上合理的推广，允许通过图卷积运算将各种知识嵌入方法结合到实体和关系的面向任务嵌入中。特别是为了获取知识图中异构关系的丰富语义，我们的模型中的实体嵌入和关系嵌入都被用来在递归聚合过程中加强彼此的优化。图1说明了以前的工作和我们的模型之间的主要差异。