积跬步至千里 || 矩阵可视化

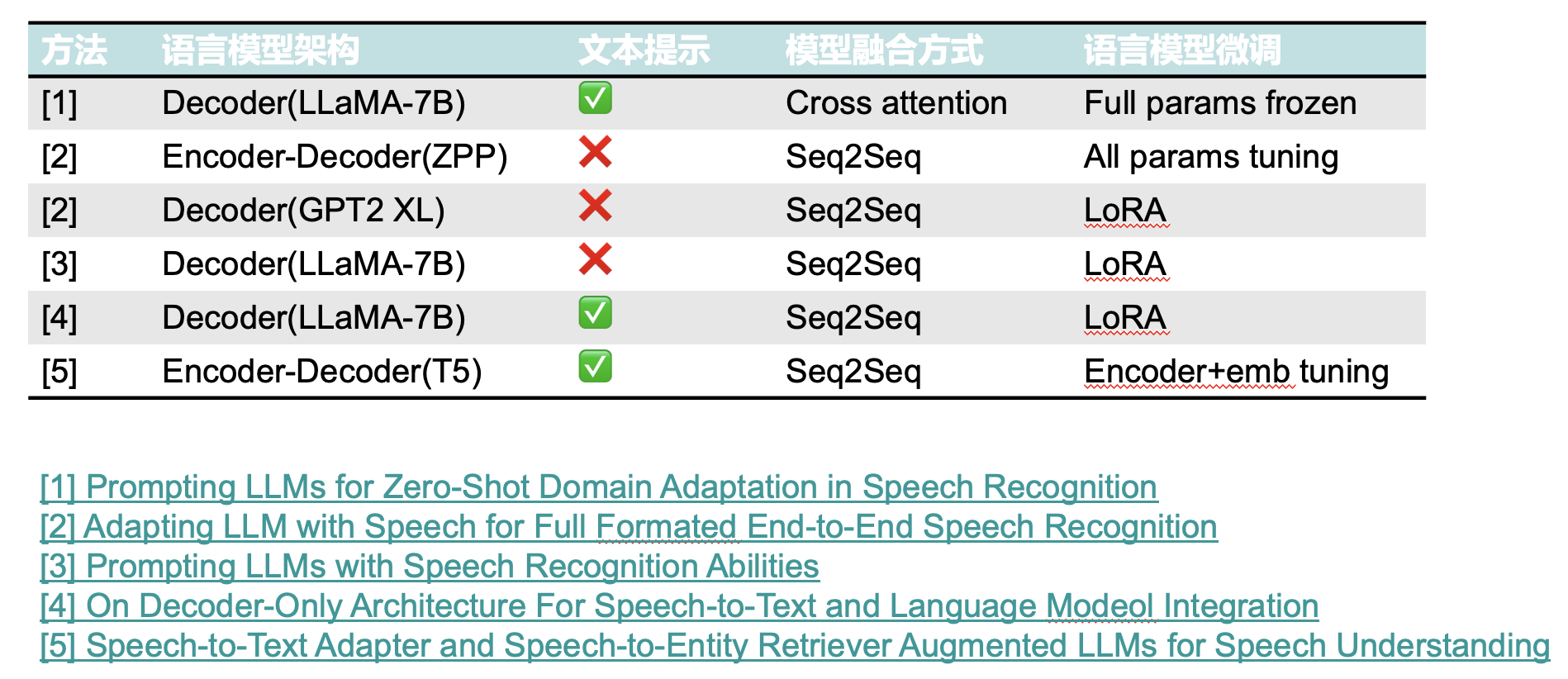
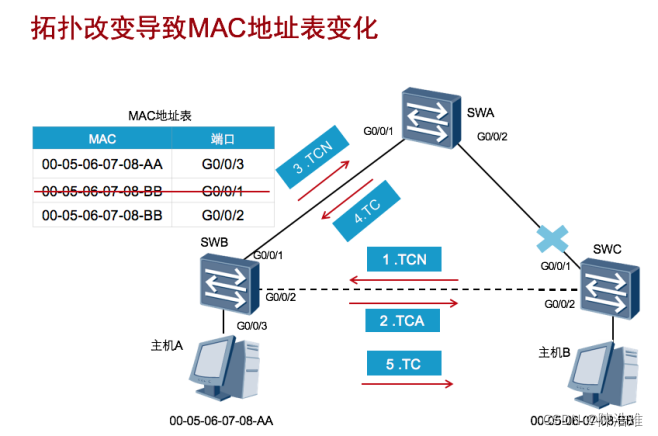
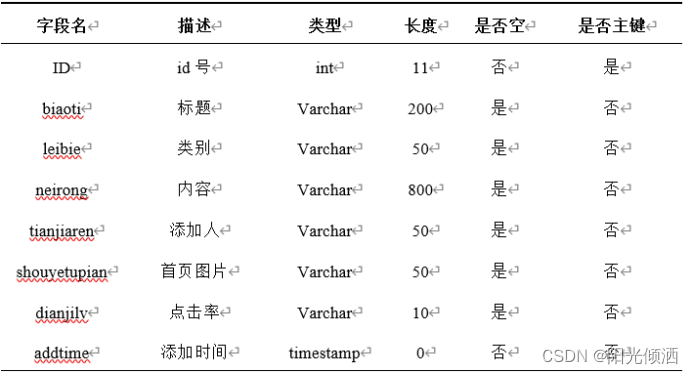
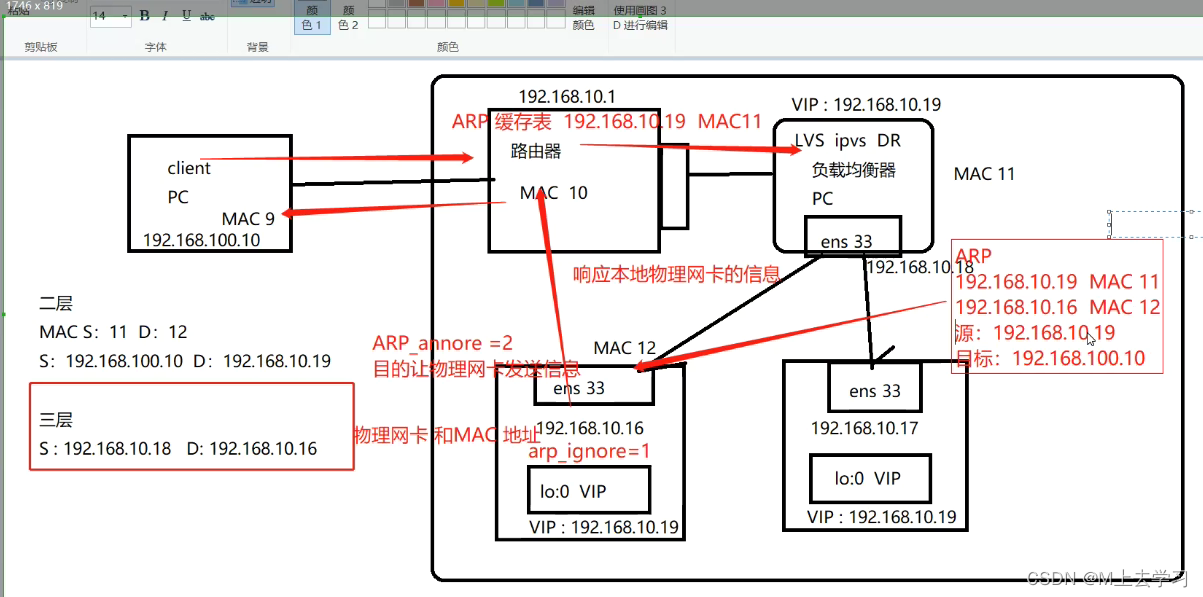
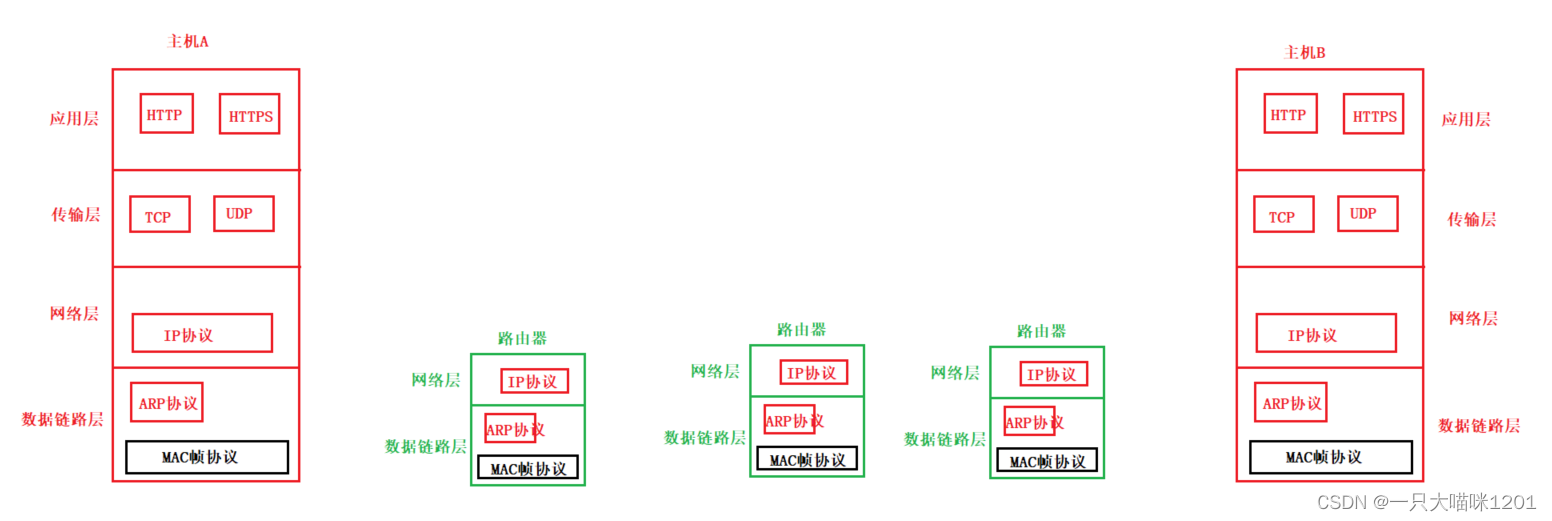
矩阵可视化

矩阵可以很方面地展示事物两两之间的关系，这种关系可以通过矩阵可视化的方式进行简单监控。

定义一个通用类

from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pdclass matrix_monitor():def __init__(self,min_color=-1,max_color=1,grad=5):self.min_color = min_colorself.max_color = max_colorself.grad = graddef fit_transform(self,Matrix):data = pd.DataFrame(Matrix)#设置色条的刻度：tick_=np.arange(self.min_color, self.max_color, self.grad).astype(float)#编辑做为参数的字典：dict_={'orientation':'vertical',"label":"color  \scale","drawedges":True,"ticklocation":"top","extend":"min", \"filled":True,"alpha":0.8,"cmap":"cmap","ticks":tick_}#将字典传入给参数cbar_kws:cmap=sns.heatmap(data,cbar_kws=dict_,center=0.5)plt.show()

调用类

import numpy as npX = data=np.random.randn(100,10)model = matrix_monitor()
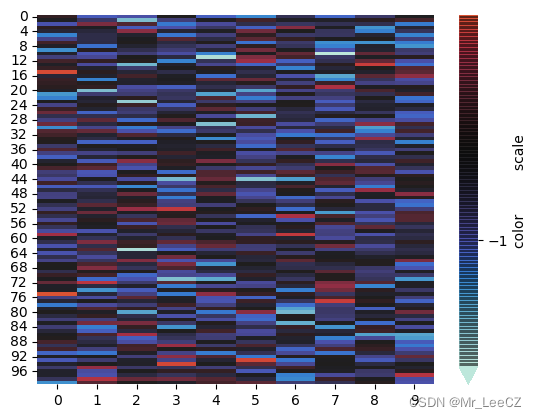
model.fit_transform(X)

结果展示
在这里插入图片描述

另一种方法

# -*- coding: utf-8 -*-
# @Time    : 2022/9/24 16:33
# @Author  : ***
# @E-mail  : ***
# @File    : draw_heatmap.pyimport numpy as np
import matplotlib.pyplot as plt
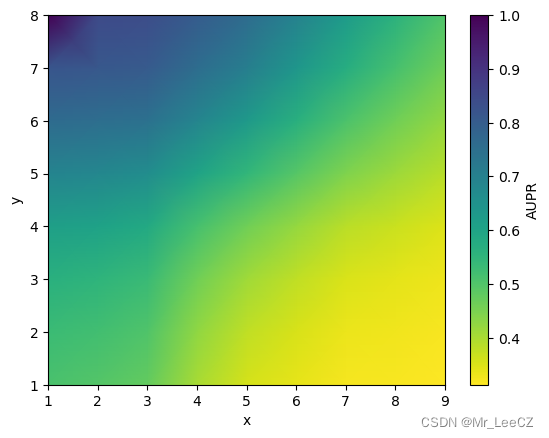
from scipy.interpolate import griddataif __name__ == '__main__':X, Y = np.meshgrid(np.arange(9,0,-1),np.arange(8,0,-1))z = np.array([[0.50183977, 0.561332835, 0.625160768, 0.69396128, 0.759163978, 0.802044391, 0.839099501, 0.845485988,1, ],[0.464608121, 0.514854349, 0.571697125, 0.638777513, 0.707394237, 0.757547047, 0.805266426,0.814383193, 0.819529712, ],[0.42307737, 0.46231148, 0.507083231, 0.566034365, 0.631072187, 0.686196609, 0.743523975, 0.755396779,0.762416452, ],[0.385141269, 0.4129182, 0.44453635, 0.492440329, 0.54721264, 0.601517055, 0.666135176, 0.680423041,0.689101386, ],[0.349207249, 0.366696746, 0.384802277, 0.420102726, 0.461066828, 0.515066771, 0.585729701,0.603058967, 0.613716782, ],[0.330000562, 0.341282639, 0.351972084, 0.379004624, 0.410013296, 0.460646534, 0.534264624,0.553158381, 0.564695194, ],[0.319270694, 0.327231515, 0.333579852, 0.35462508, 0.378290545, 0.426066004, 0.500875256,0.520510426, 0.532623573, ],[0.312393427, 0.31783125, 0.321113142, 0.338438575, 0.357088955, 0.401471861, 0.477147046,0.497178064, 0.509567816, ],])c = plt.pcolormesh(X, Y, z, cmap='viridis_r', shading='gouraud')# 彩虹热力图# c = plt.pcolormesh(x_r, y_r, z, cmap='viridis_r')# 普通热力图plt.colorbar(c, label='AUPR')plt.xlabel('x')plt.ylabel('y')
#    plt.savefig('heatmap.tif', dpi=300)plt.show()