[保研/考研机试] KY124 二叉搜索树浙江大学复试上机题 C++实现

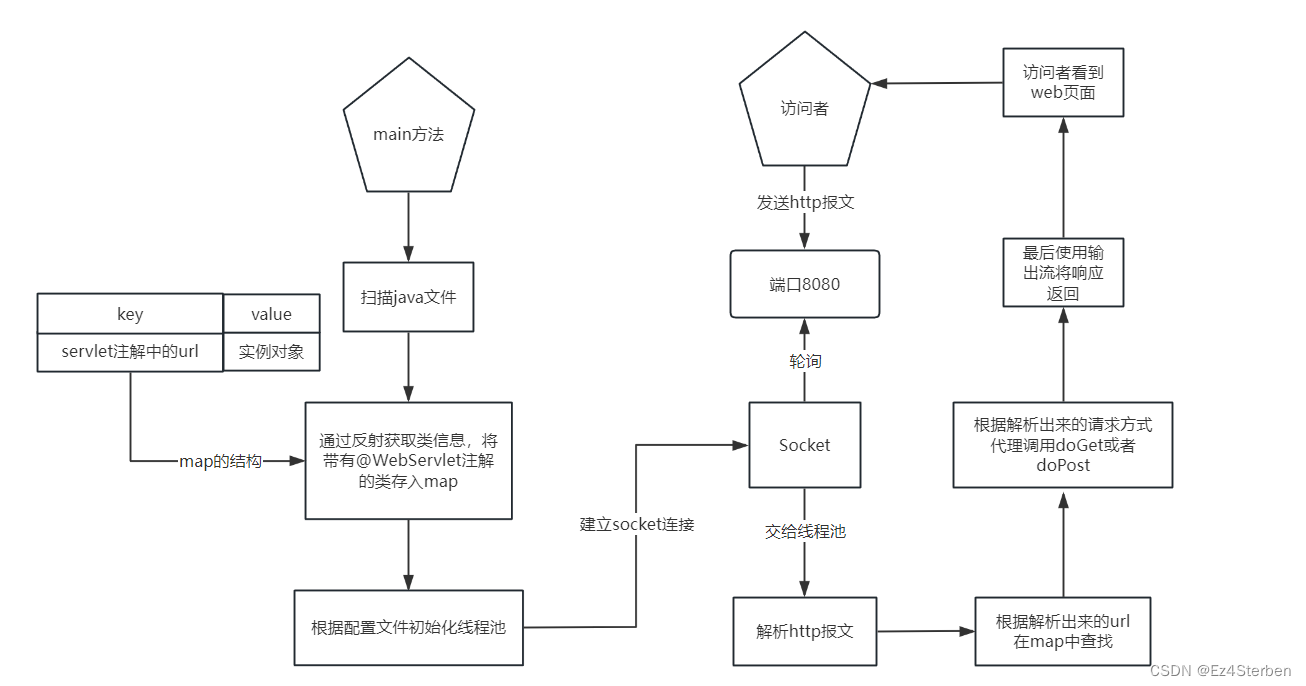
题目链接：

二叉搜索树_牛客题霸_牛客网判断两序列是否为同一二叉搜索树序列。题目来自【牛客题霸】https://www.nowcoder.com/share/jump/437195121692722892652

描述

判断两序列是否为同一二叉搜索树序列

输入描述：

开始一个数n，(1<=n<=20) 表示有n个需要判断，n= 0 的时候输入结束。接下去一行是一个序列，序列长度小于10，包含(0~9)的数字，没有重复数字，根据这个序列可以构造出一颗二叉搜索树。接下去的n行有n个序列，每个序列格式跟第一个序列一样，请判断这两个序列是否能组成同一颗二叉搜索树。

输出描述：

如果序列相同则输出YES，否则输出NO

示例1：

输入:

输出:

YES
NO

方法1思路：

定义了二叉搜索树节点结构 TreeNode，包含数据域 data，左子节点指针 leftChild，右子节点指针 rightChild。
Insert 函数用于将字符插入到二叉搜索树中，根据大小关系将字符插入左子树或右子树中。
PreOrder 函数实现了先序遍历，将遍历结果存入向量 v 中。
在 main 函数中，首先读取一个整数 n，表示要进行的测试用例数量。
对于每个测试用例，读取第一棵树的字符序列，构建二叉搜索树，然后对其进行先序遍历，将结果存入向量 v1 中。
读取第二棵树的字符序列，同样构建二叉搜索树，进行先序遍历，将结果存入向量 v2 中。
将向量 v1 与向量 v2 逐一比较，如果有不同的元素，则结果标志设为 NO，否则设为 YES，最后输出结果标志。

方法1源代码：

#include<iostream>
#include<string>
#include<vector>
using namespace std;// 定义二叉搜索树节点结构
struct TreeNode {char data; // 节点数据TreeNode* leftChild; // 左子节点指针TreeNode* rightChild; // 右子节点指针TreeNode(char c) : data(c), leftChild(NULL), rightChild(NULL) {} // 构造函数
};// 将字符插入到二叉搜索树中
TreeNode* Insert(TreeNode* root, char x) {if (root == NULL) {root = new TreeNode(x); // 创建新节点}else if (x < root->data) {root->leftChild = Insert(root->leftChild, x); // 向左子树插入}else if (x > root->data) {root->rightChild = Insert(root->rightChild, x); // 向右子树插入}return root;
}// 先序遍历，将遍历结果存入向量 v
void PreOrder(TreeNode* root, vector<char>& v) {if (root == NULL) {return;}PreOrder(root->leftChild, v); // 遍历左子树PreOrder(root->rightChild, v); // 遍历右子树v.push_back(root->data); // 将节点数据存入向量
}int main() {int n;while (cin >> n) {if (n == 0) {break;}string s1;cin >> s1;vector<char> v1; // 存储第一棵树的先序遍历结果TreeNode* tree1 = NULL; // 第一棵树的根节点if (s1 != "") {for (int i = 0; i < s1.size(); i++) {tree1 = Insert(tree1, s1[i]); // 将字符插入第一棵树中}PreOrder(tree1, v1); // 对第一棵树进行先序遍历，并将结果存入 v1}for (int i = 0; i < n; i++) {string s2;cin >> s2;if (s1 == "" && s2 == "") {cout << "YES" << endl; // 如果两棵树都为空，输出 YESbreak;}if (s1 == "" || s2 == "") {cout << "NO" << endl; // 如果其中一棵树为空，输出 NObreak;}vector<char> v2; // 存储第二棵树的先序遍历结果TreeNode* tree2 = NULL; // 第二棵树的根节点for (int i = 0; i < s2.size(); i++) {tree2 = Insert(tree2, s2[i]); // 将字符插入第二棵树中}PreOrder(tree2, v2); // 对第二棵树进行先序遍历，并将结果存入 v2string flag = "YES"; // 初始化结果标志为 YESfor (int i = 0; i < v1.size(); i++) {if (v1[i] != v2[i]) {flag = "NO"; // 如果两棵树的先序遍历结果不同，将结果标志设为 NObreak;}}cout << flag << endl; // 输出结果标志}}return 0;
}

方法2思路：

定义了二叉树节点结构 TreeNode，包含数据域 data，左子节点指针 leftChild，右子节点指针 rightChild。
Insert 函数用于将字符插入到二叉树中。根据字符大小关系，字符被插入到左子树或右子树中。
isSame 函数判断两棵二叉树是否相同。递归判断两棵二叉树的节点数据、左子树和右子树是否相同。
在 main 函数中，首先读取一个整数 n，表示要比较的二叉树个数。然后读取第一颗二叉树的先序遍历结果，并将字符插入到二叉树中。接着循环读取第二颗二叉树的先序遍历结果，将字符插入到二叉树中，并调用 isSame 函数判断两棵二叉树是否相同，输出对应结果。

方法2源代码：

#include<iostream>
#include<string>
#include<vector>
using namespace std;// 定义二叉树节点结构
struct TreeNode {char data; // 节点数据TreeNode* leftChild; // 左子节点指针TreeNode* rightChild; // 右子节点指针TreeNode(char c) : data(c), leftChild(NULL), rightChild(NULL) {} // 构造函数
};// 将字符插入到二叉树中
TreeNode* Insert(TreeNode* root, char x) {if (root == NULL) {root = new TreeNode(x); // 创建新节点}else if (x < root->data) {root->leftChild = Insert(root->leftChild, x); // 插入到左子树}else if (x > root->data) {root->rightChild = Insert(root->rightChild, x); // 插入到右子树}return root;
}// 判断两棵二叉树是否相同
bool isSame(TreeNode* root1, TreeNode* root2) {if (root1 == NULL && root2 == NULL) {return true; // 两个为空，相同}if (root1 == NULL || root2 == NULL) {return false; // 一个为空，一个不为空，不相同}if (root1->data != root2->data) {return false; // 节点数据不同，不相同}// 递归判断左子树和右子树return isSame(root1->leftChild, root2->leftChild) && isSame(root1->rightChild, root2->rightChild);
}int main() {int n;while (cin >> n) {if (n == 0) {break;}string s1;cin >> s1; // 读取第一颗二叉树的先序遍历结果TreeNode* root1 = NULL;for (int i = 0; i < s1.size(); i++) {root1 = Insert(root1, s1[i]); // 将字符插入到第一颗二叉树中}for (int i = 0; i < n; i++) {string s2;cin >> s2; // 读取第二颗二叉树的先序遍历结果TreeNode* root2 = NULL;for (int i = 0; i < s2.size(); i++) {root2 = Insert(root2, s2[i]); // 将字符插入到第二颗二叉树中}bool res = isSame(root1, root2); // 判断两棵二叉树是否相同if (res) {cout << "YES" << endl; // 输出结果}else {cout << "NO" << endl; // 输出结果}}}return 0;
}