1. 数学基础

1.1 标量和向量

标量 Scalar
一个标量就是一个单独的数

向量 Vector
一个向量是一列数
可以把向量看做空间中的点，每个元素是不同坐标轴上的坐标
向量中有几个数，就叫几维向量
如4维向量：[1,2,3,4]

1.2 向量运算

向量加和: A +B = B + A 需要维度相同
[1,2] + [3,4] = [4, 6]

向量内积: A * B = B * A 需要维度相同
[1,2] * [3, 4] = 1 * 3 + 2* 4 = 11

1.3 矩阵

矩阵 matrix
是一个二维数组。矩阵中的每一个值是一个标量，可以通过行号和列号进行索引
矩阵加法 需要维度相同

矩阵乘法
不满足交换律 A * B != B* A
当左矩阵A的列数等于右矩阵B的行数时，A与B可以相乘
M x N 矩阵乘以 N x P矩阵得到M x P维度矩阵

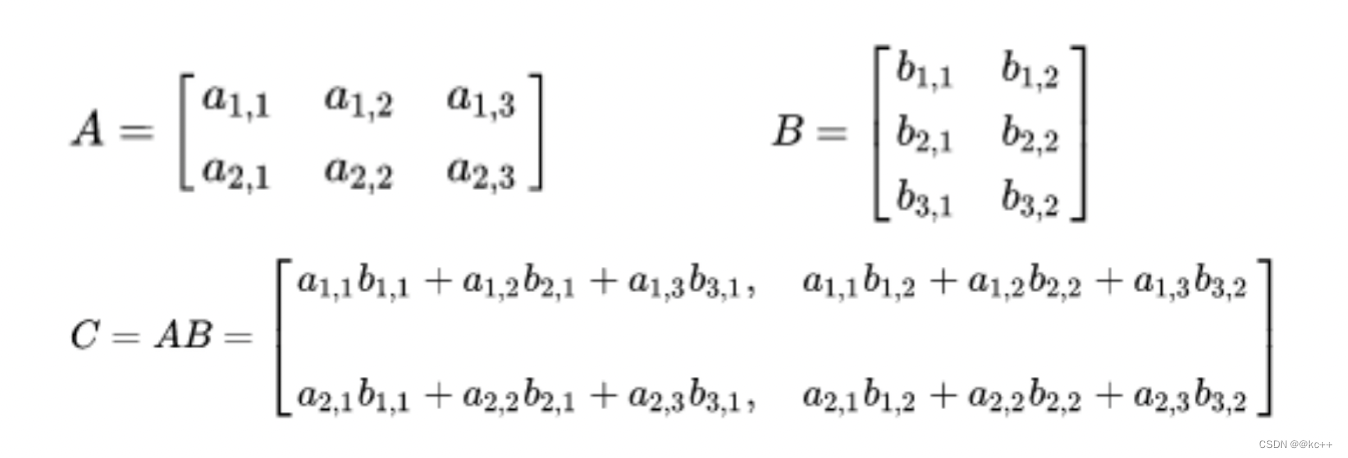
符合分配律
A*(B+C) = A*B + A * C

符合结合律
A * (B * C) = (A * B) * C

另一种矩阵乘法 – 矩阵点乘
两矩阵必须形状一致

1.4 张量

张量 tensor
将三个2 x 2的矩阵排列在一起，就可以称为一个 3 x 2 x 2的张量
将4个3 x 2 x 2的张量排列在一起，就可以成为一个 4 x 3 x 2 x 2维度的张量。
张量是神经网络的训练中最为常见的数据形式。
所有的输入，输出，中间结果，几乎都是以张量的形式存在。

1.5 导数

导数表示函数变化的方向

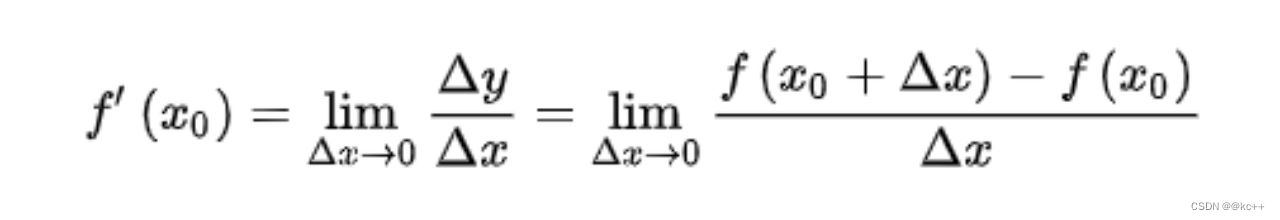
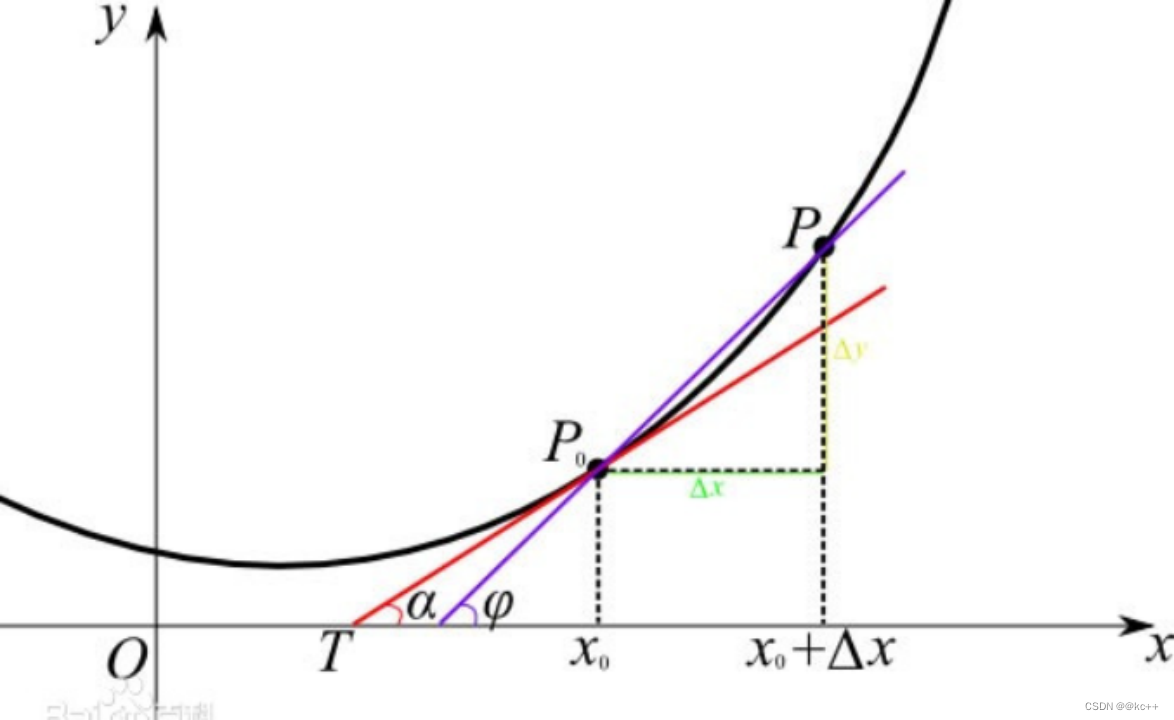
常见导数

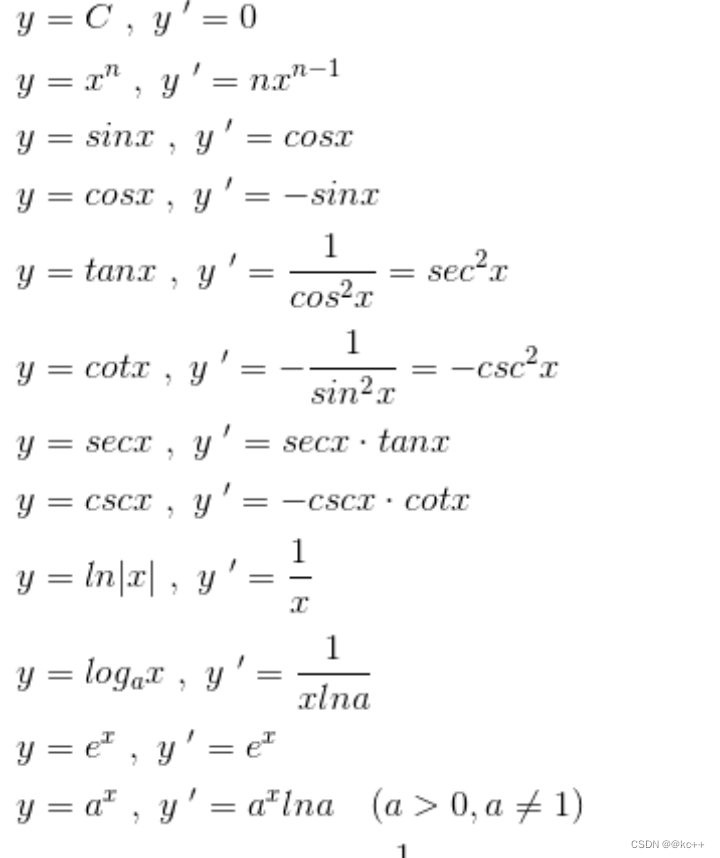
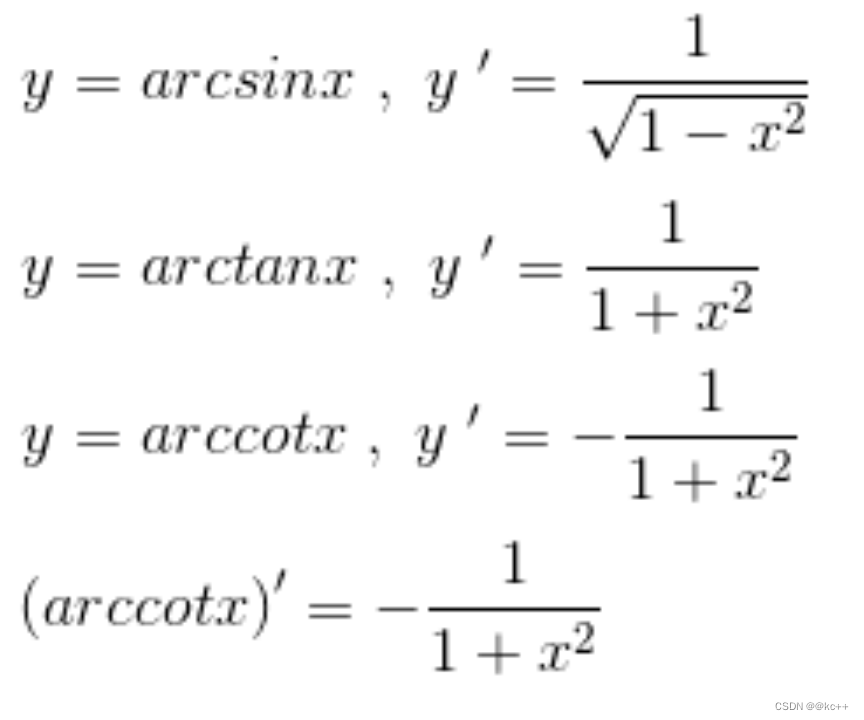
求导法则
加（减）法则：[f(x)+g(x)]‘=f(x)’+g(x)’

乘法法则：[f(x)*g(x)]‘=f(x)’*g(x)+g(x)'*f(x)

除法法则：[f(x)/g(x)]‘=[f(x)’*g(x)-g(x)'*f(x)]/g(x)2

链式法则：若h(x)=f(g(x))，则h’(x)=f’(g(x))g’(x)

2. numpy常用操作

NumPy 是 Python 中的一个开源库，提供大量的数学函数和多维数组对象，以及各种派生对象（如掩码数组和矩阵），这些工具可用于各种数学和逻辑操作。它是大多数数据科学和科学计算Python工具的基础。

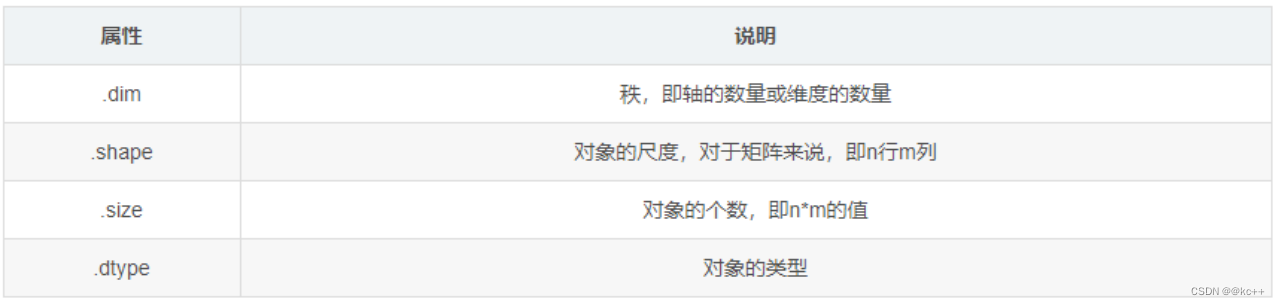
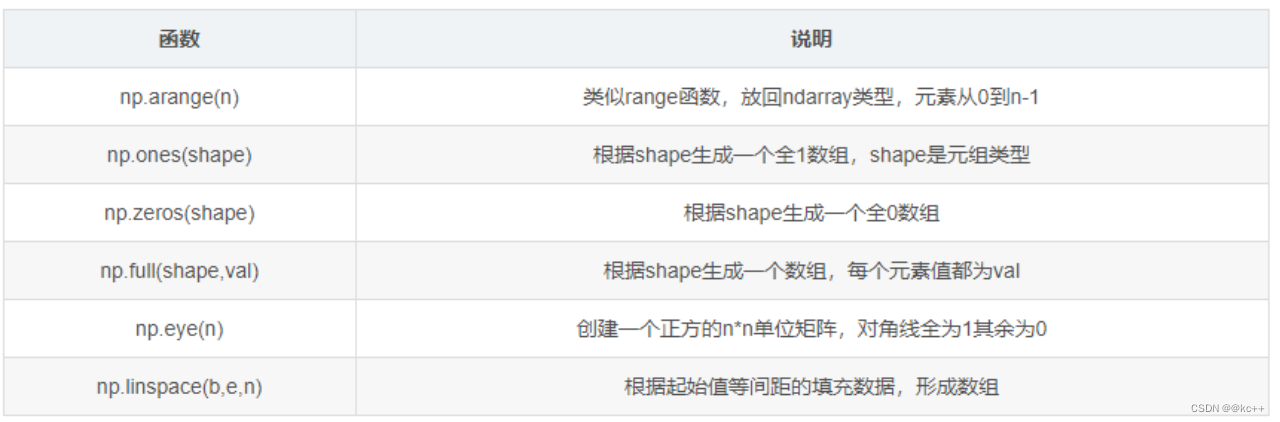
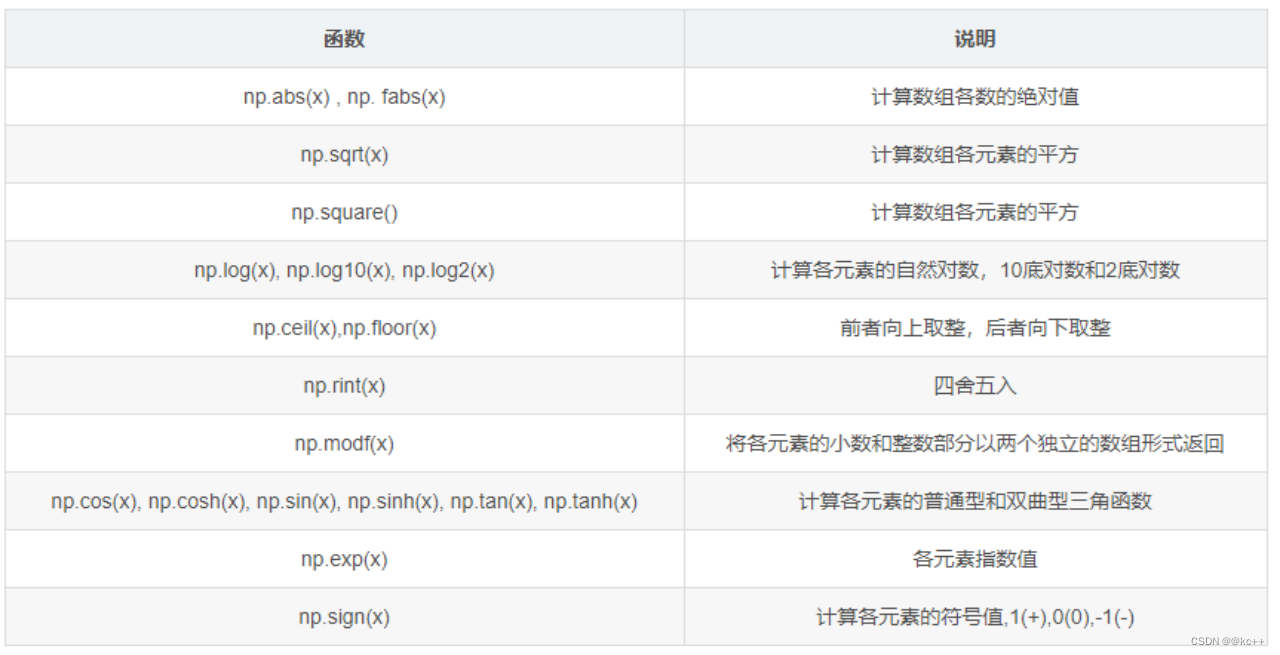
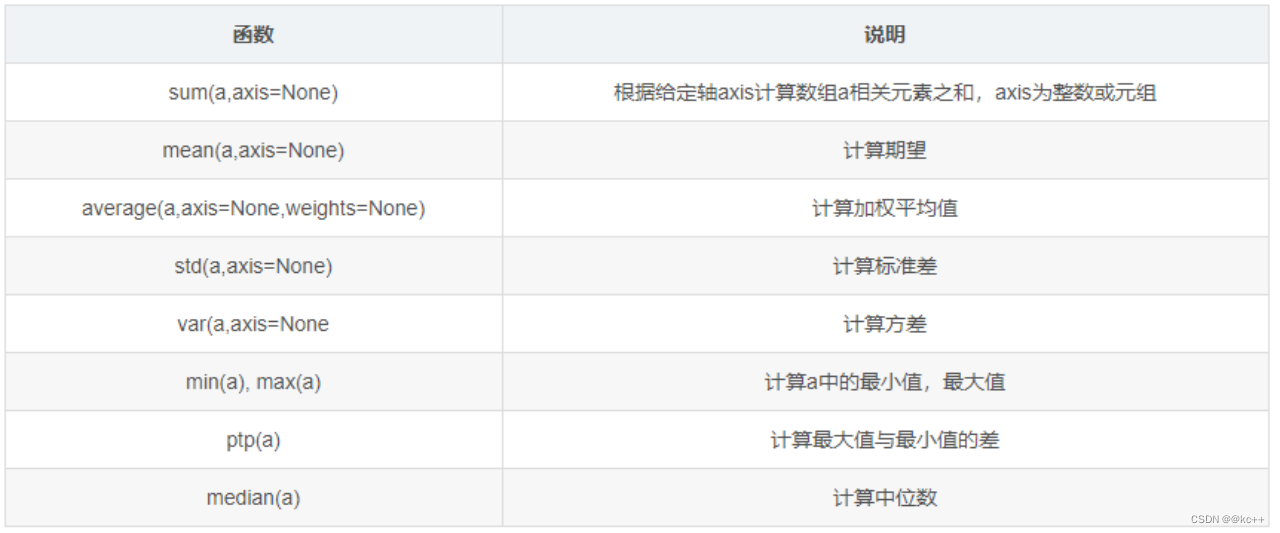
代码示例

#coding:utf8import torch
import numpy as np#numpy基本操作
x = np.array([[1,2,3],[4,5,6]])
#
print(x.ndim)
print(x.shape)
print(x.size)
print(np.sum(x))
print(np.sum(x, axis=0))
print(np.sum(x, axis=1))
print(np.reshape(x, (3,2)))
print(np.sqrt(x))
print(np.exp(x))
print(x.transpose())
print(x.flatten())#
# print(np.zeros((3,4,5)))
# print(np.random.rand(3,4,5))
#
# x = np.random.rand(3,4,5)
x = torch.FloatTensor(x)
print(x.shape)
print(torch.exp(x))
print(torch.sum(x, dim=0))
print(torch.sum(x, dim=1))
print(x.transpose(1, 0))
print(x.flatten())

3. 梯度下降算法

梯度下降算法是一个用于寻找函数最小值的迭代优化算法。在机器学习和深度学习中，通常使用梯度下降来优化损失函数，从而训练模型的参数。

梯度下降的核心思想是使用函数的梯度（或近似梯度）来确定在函数值减小的方向上迭代更新参数。换句话说，如果你站在山坡上并想找到最短的路径下山，那么在每一步，你应该朝着最陡峭的下坡方向走。

算法步骤：

1. 初始化参数（通常是随机的）。
2. 计算损失函数的梯度。
3. 更新参数，使其沿着梯度的负方向移动：
   θ=θ−α×∇θ ，其中 α 是学习率。
4. 重复步骤 2 和 3，直到满足停止准则（例如，梯度接近于零，达到最大迭代次数，或损失变化很小）。

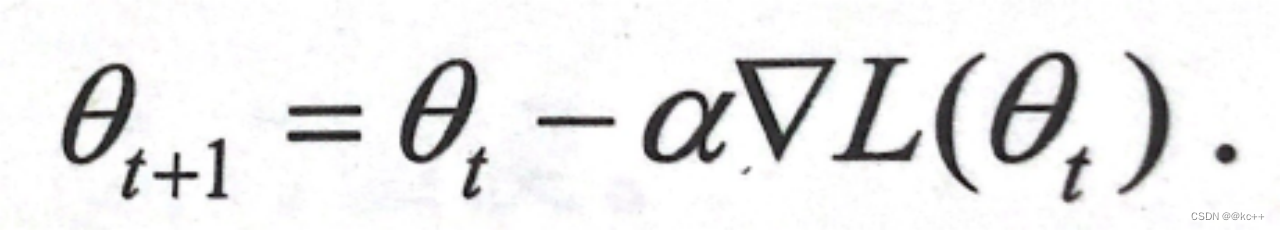
学习率 α 决定了每次迭代时参数更新的步长。太大的学习率可能会使算法在最小值附近震荡，而太小的学习率可能会导致算法收敛得太慢。很多高级的优化算法（如 Adam、RMSprop 等）都是为了在训练过程中自动调整学习率。

权重更新方式

Gradient descent
所有样本一起计算梯度（累加）

Stochastic gradient descent
每次使用一个样本计算梯度

Mini-batch gradient descent
每次使用n个样本计算梯度（累加）

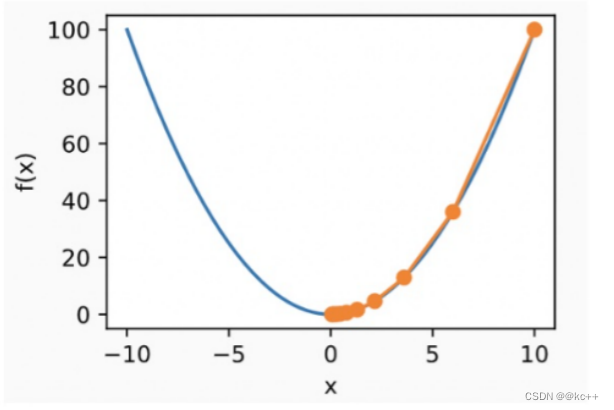
找极小值问题

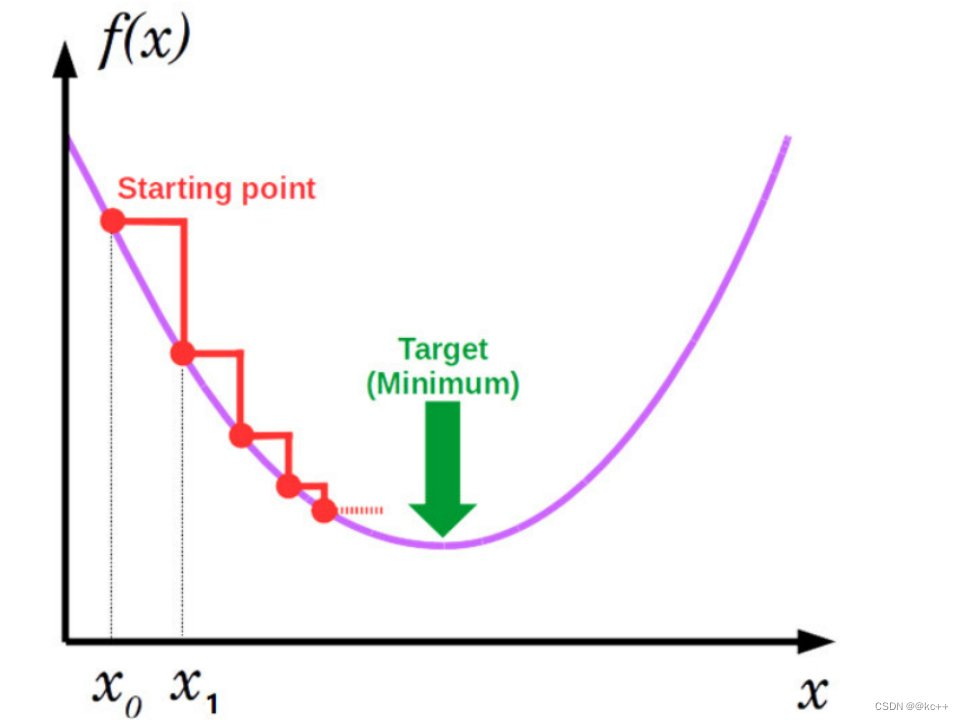
函数f(x)的值受x影响

目标：找到合适的x值，使得f(x)最小

方法：

1. 任取一点x0，计算在这一点的导数值f(x0)
2. 根据导数的正负，决定x0应当调大还是调小
3. 迭代进行1,2直到x不在变化（或变化极小）

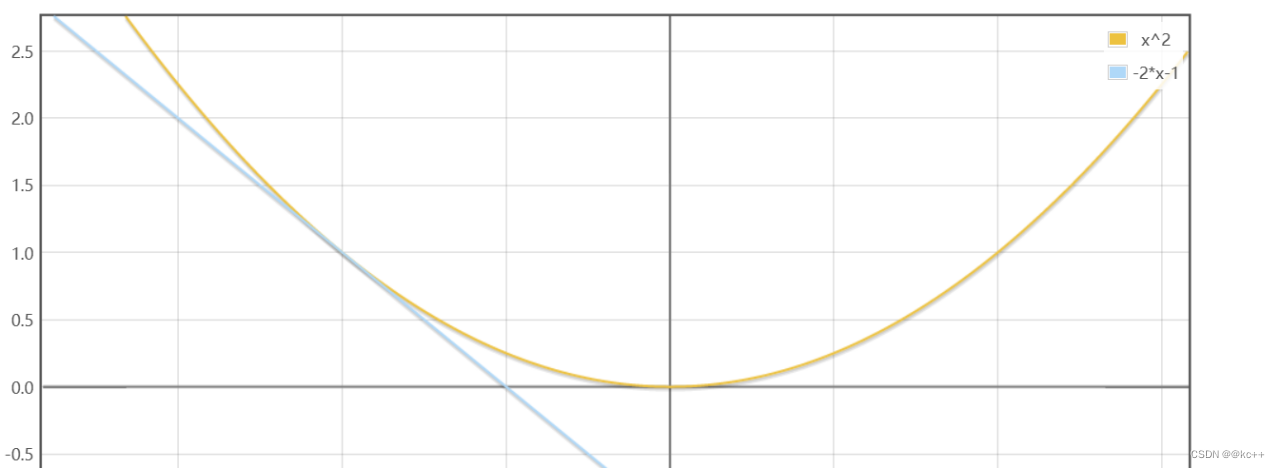
原函数为 y = x2 导函数为 y = 2*x
在x = -1这个点，导数值为 -2
该点导数为负数，说明在这一点，如果x增大，y会减小
所以f(x)最小值的点应当在-1的右侧（大于-1）

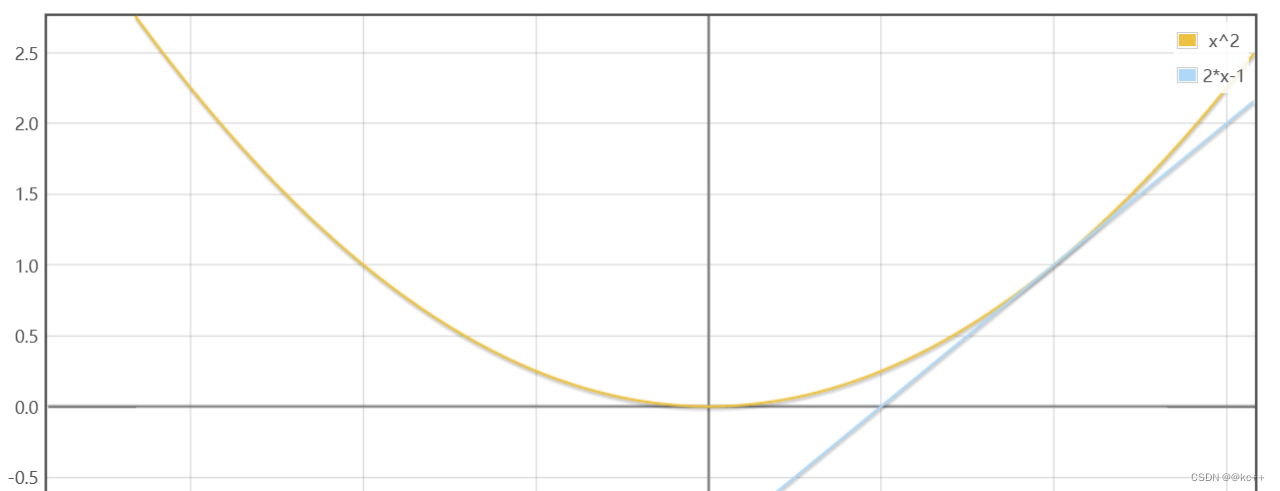
原函数为 y = x2 导函数为 y = 2*x
在x = 1这个点，导数值为 2
该点导数为正数，说明在这一点，如果x增大，y会增大
所以f(x)最小值的点应当在-1的左侧（小于1）

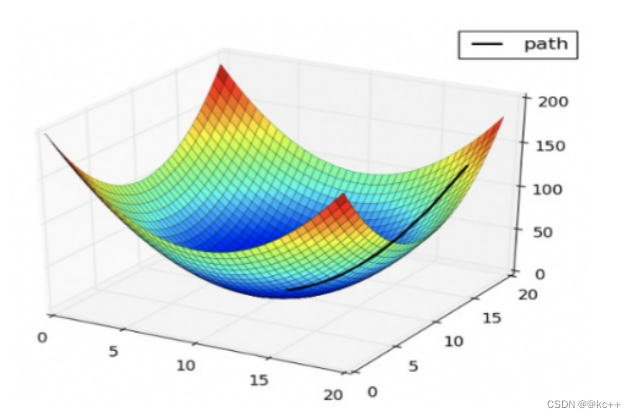
梯度

• 梯度：可以理解为多元函数的导数，意义与导数基本一致

原函数：y = 3x2
导函数: y = 6x
在x=1处的导数值：6

原函数：y = 3x12 + 4x22 + 5x32
导函数：y = {6x1 , 8x2 , 10x3}
在[1，1，1]处的梯度是[6，8，10]
梯度是个向量

4. 反向传播

4.1 完整的反向传播过程

1. 根据输入x和模型当前权重，计算预测值y’
2. 根据y’和y使用loss函数计算loss
3. 根据loss计算模型权重的梯度
4. 使用梯度和学习率，根据优化器调整模型权重

4.2 代码演示

# coding:utf8import torch
import torch.nn as nn
import numpy as np
import copy"""
基于pytorch的网络编写
手动实现梯度计算和反向传播
加入激活函数
"""class TorchModel(nn.Module):def __init__(self, hidden_size):super(TorchModel, self).__init__()self.layer = nn.Linear(hidden_size, hidden_size, bias=False)self.activation = torch.sigmoidself.loss = nn.functional.mse_loss  # loss采用均方差损失# 当输入真实标签，返回loss值；无真实标签，返回预测值def forward(self, x, y=None):y_pred = self.layer(x)y_pred = self.activation(y_pred)if y is not None:return self.loss(y_pred, y)else:return y_pred# 自定义模型，接受一个参数矩阵作为入参
class DiyModel:def __init__(self, weight):self.weight = weightdef forward(self, x, y=None):y_pred = np.dot(self.weight, x)y_pred = self.diy_sigmoid(y_pred)if y is not None:return self.diy_mse_loss(y_pred, y)else:return y_pred# sigmoiddef diy_sigmoid(self, x):return 1 / (1 + np.exp(-x))# 手动实现mse，均方差lossdef diy_mse_loss(self, y_pred, y_true):return np.sum(np.square(y_pred - y_true)) / len(y_pred)# 手动实现梯度计算def calculate_grad(self, y_pred, y_true, x):# 前向过程# wx = np.dot(self.weight, x)# sigmoid_wx = self.diy_sigmoid(wx)# loss = self.diy_mse_loss(sigmoid_wx, y_true)# 反向过程# 均方差函数 (y_pred - y_true) ^ 2 / n 的导数 = 2 * (y_pred - y_true) / ngrad_loss_sigmoid_wx = 2/len(x) * (y_pred - y_true)# sigmoid函数 y = 1/(1+e^(-x)) 的导数 = y * (1 - y)grad_sigmoid_wx_wx = y_pred * (1 - y_pred)# wx对w求导 = xgrad_wx_w = x# 导数链式相乘grad = grad_loss_sigmoid_wx * grad_sigmoid_wx_wxgrad = np.dot(grad.reshape(len(x), 1), grad_wx_w.reshape(1, len(x)))return grad# 梯度更新def diy_sgd(grad, weight, learning_rate):return weight - learning_rate * grad# adam梯度更新def diy_adam(grad, weight):# 参数应当放在外面，此处为保持后方代码整洁简单实现一步alpha = 1e-3  # 学习率beta1 = 0.9  # 超参数beta2 = 0.999  # 超参数eps = 1e-8  # 超参数t = 0  # 初始化mt = 0  # 初始化vt = 0  # 初始化# 开始计算t = t + 1gt = gradmt = beta1 * mt + (1 - beta1) * gtvt = beta2 * vt + (1 - beta2) * gt ** 2mth = mt / (1 - beta1 ** t)vth = vt / (1 - beta2 ** t)weight = weight - (alpha / (np.sqrt(vth) + eps)) * mthreturn weightx = np.array([1, 2, 3, 4])  # 输入
y = np.array([0.1, -0.1, 0.01, -0.01])  # 预期输出# torch实验
torch_model = TorchModel(len(x))
torch_model_w = torch_model.state_dict()["layer.weight"]
print(torch_model_w, "初始化权重")
numpy_model_w = copy.deepcopy(torch_model_w.numpy())
# numpy array -> torch tensor, unsqueeze的目的是增加一个batchsize维度
torch_x = torch.from_numpy(x).float().unsqueeze(0)
torch_y = torch.from_numpy(y).float().unsqueeze(0)
# torch的前向计算过程，得到loss
torch_loss = torch_model(torch_x, torch_y)
print("torch模型计算loss：", torch_loss)
# #手动实现loss计算
diy_model = DiyModel(numpy_model_w)
diy_loss = diy_model.forward(x, y)
print("diy模型计算loss：", diy_loss)# #设定优化器
learning_rate = 0.1
optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate)
# optimizer = torch.optim.Adam(torch_model.parameters())
optimizer.zero_grad()
#
# #pytorch的反向传播操作
torch_loss.backward()
print(torch_model.layer.weight.grad, "torch 计算梯度")  # 查看某层权重的梯度# #手动实现反向传播
grad = diy_model.calculate_grad(diy_model.forward(x), y, x)
print(grad, "diy 计算梯度")
#
# #torch梯度更新
# optimizer.step()
# #查看更新后权重
# update_torch_model_w = torch_model.state_dict()["layer.weight"]
# print(update_torch_model_w, "torch更新后权重")
#
# #手动梯度更新
# diy_update_w = diy_sgd(grad, numpy_model_w, learning_rate)
# diy_update_w = diy_adam(grad, numpy_model_w)
# print(diy_update_w, "diy更新权重")

5. 网络结构 – 全连接层

全连接层又称线性层
计算公式：y = w * x + b
W和b是参与训练的参数
W的维度决定了隐含层输出的维度，一般称为隐单元个数（hidden size）
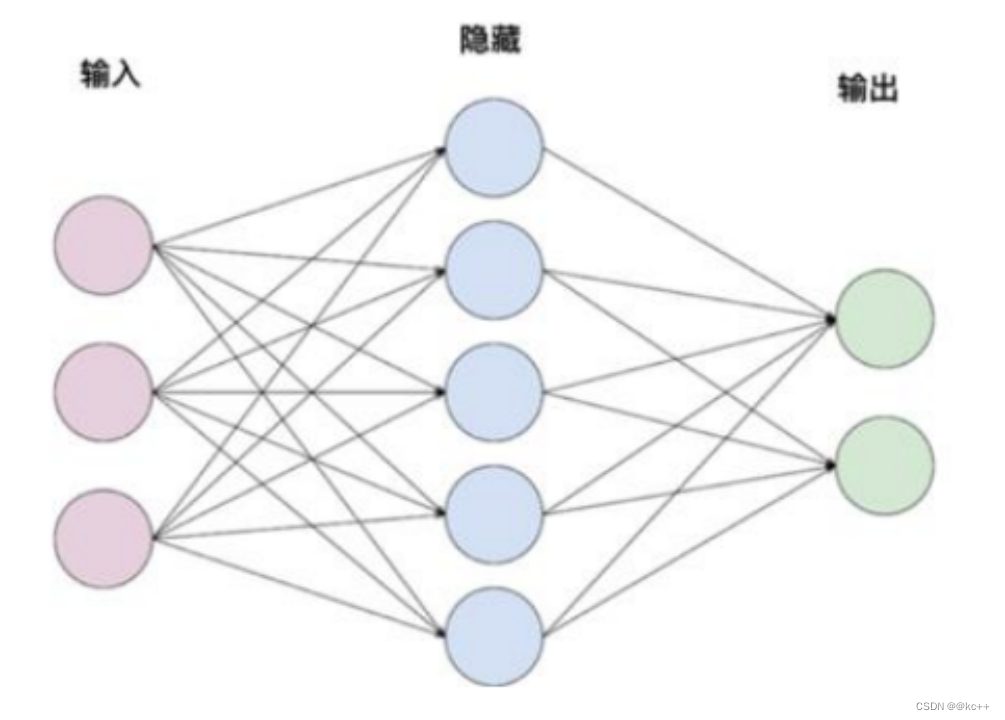
举例：
输入：x （维度1 x 3）
隐含层1：w（维度3 x 5）
隐含层2: w（维度5 x 2）

代码示例

#coding:utf8import torch
import torch.nn as nn
import numpy as np"""
numpy手动实现模拟一个线性层
"""#搭建一个2层的神经网络模型
#每层都是线性层
class TorchModel(nn.Module):def __init__(self, input_size, hidden_size1, hidden_size2):super(TorchModel, self).__init__()self.layer1 = nn.Linear(input_size, hidden_size1)self.layer2 = nn.Linear(hidden_size1, hidden_size2)def forward(self, x):hidden = self.layer1(x)   #shape: (batch_size, input_size) -> (batch_size, hidden_size1)y_pred = self.layer2(hidden) #shape: (batch_size, hidden_size1) -> (batch_size, hidden_size2)return y_pred#自定义模型
class DiyModel:def __init__(self, w1, b1, w2, b2):self.w1 = w1self.b1 = b1self.w2 = w2self.b2 = b2def forward(self, x):hidden = np.dot(x, self.w1.T) + self.b1y_pred = np.dot(hidden, self.w2.T) + self.b2return y_pred#随便准备一个网络输入
x = np.array([34.1, 0.3, 1.2])
#建立torch模型
torch_model = TorchModel(len(x), 5, 2)
print(torch_model.state_dict())
print("-----------")
#打印模型权重，权重为随机初始化
torch_model_w1 = torch_model.state_dict()["layer1.weight"].numpy()
torch_model_b1 = torch_model.state_dict()["layer1.bias"].numpy()
torch_model_w2 = torch_model.state_dict()["layer2.weight"].numpy()
torch_model_b2 = torch_model.state_dict()["layer2.bias"].numpy()
print(torch_model_w1, "torch w1 权重")
print(torch_model_b1, "torch b1 权重")
print("-----------")
print(torch_model_w2, "torch w2 权重")
print(torch_model_b2, "torch b2 权重")
print("-----------")
#使用torch模型做预测
torch_x = torch.FloatTensor([x])
y_pred = torch_model.forward(torch_x)
print("torch模型预测结果：", y_pred)
#把torch模型权重拿过来自己实现计算过程
diy_model = DiyModel(torch_model_w1, torch_model_b1, torch_model_w2, torch_model_b2)
#用自己的模型来预测
y_pred_diy = diy_model.forward(np.array([x]))
print("diy模型预测结果：", y_pred_diy)

6. 激活函数

模型添加非线性因素，使模型具有拟合非线性函数的能力

6.1 激活函数-Sigmoid

一种非线性映射，将任意输入映射到0-1之间

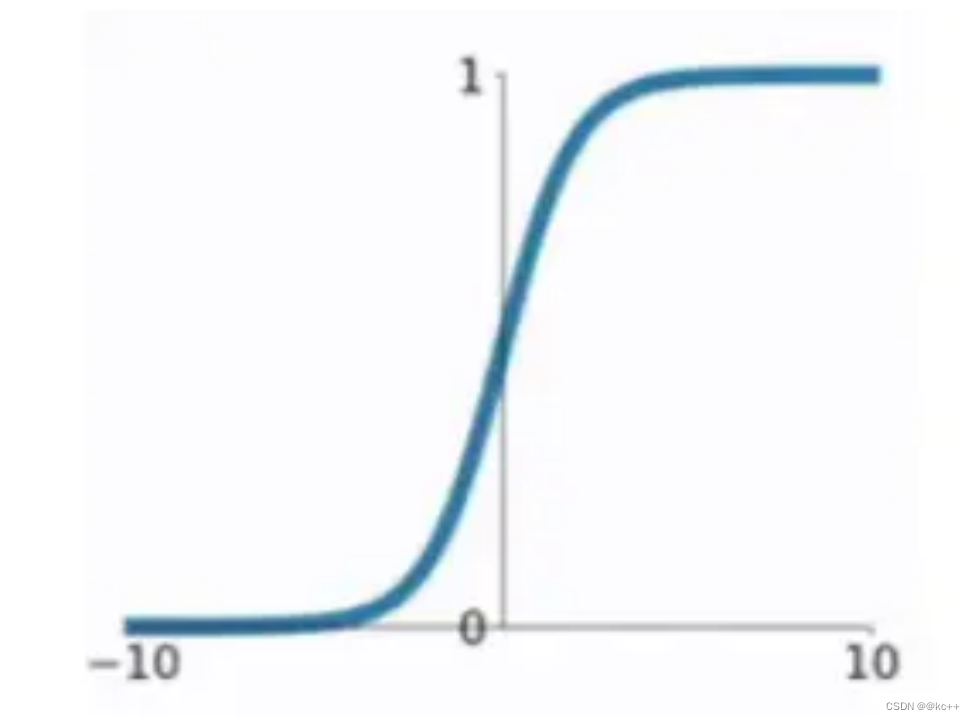
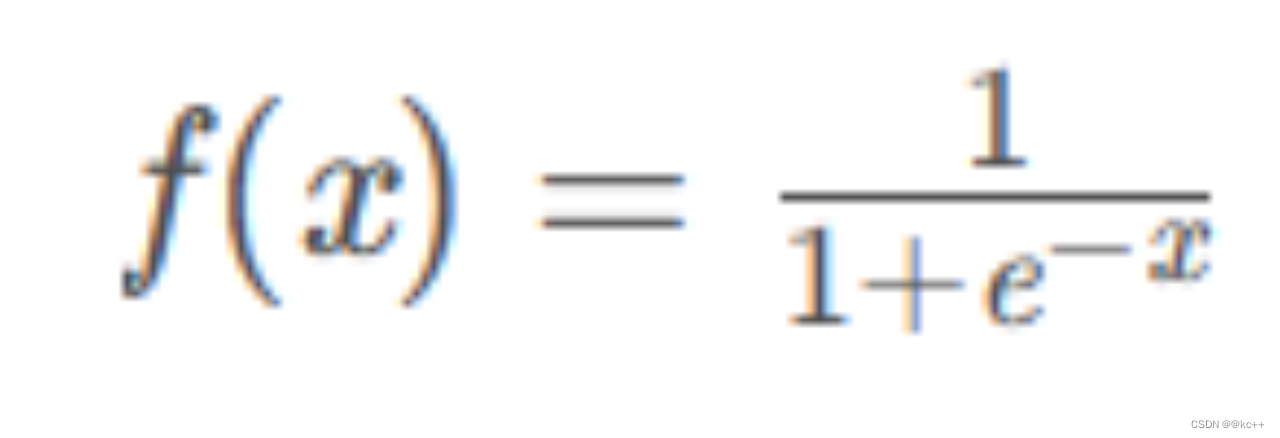
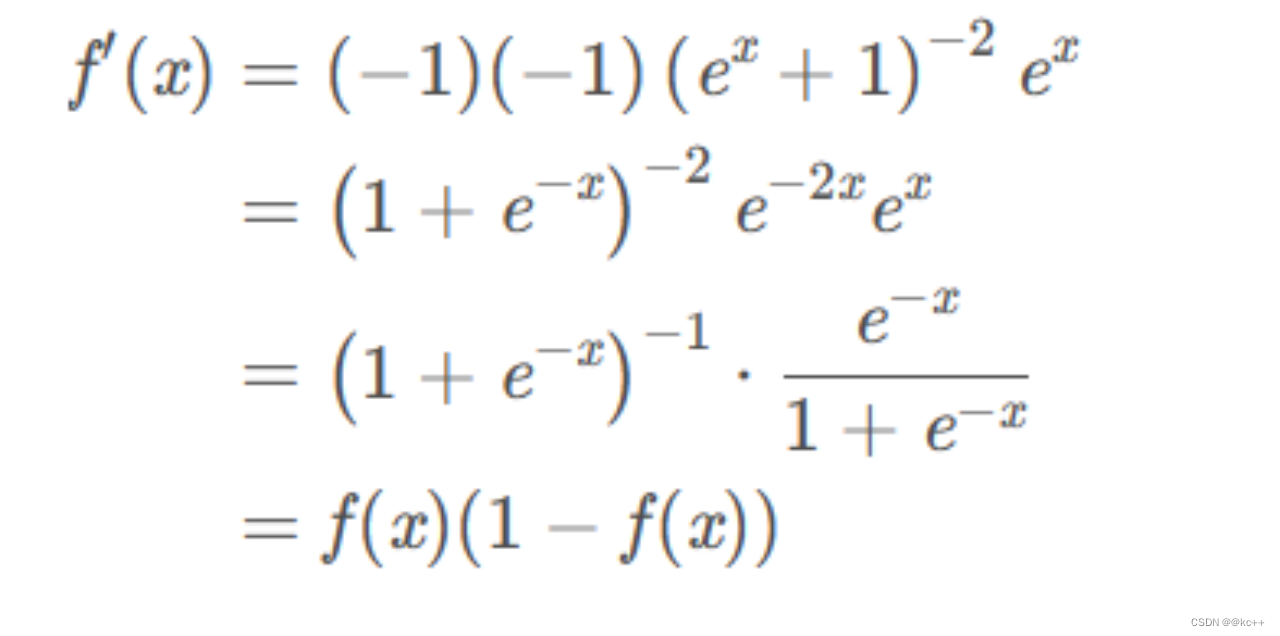
缺点：

1. 计算耗时，包含指数运算
2. 非0均值，会导致收敛慢
3. 易造成梯度消失

代码示例

import numpy as npdef sigmoid(z):return 1 / (1 + np.exp(-z))# 示例
z = np.array([-1.0, 0.0, 1.0])
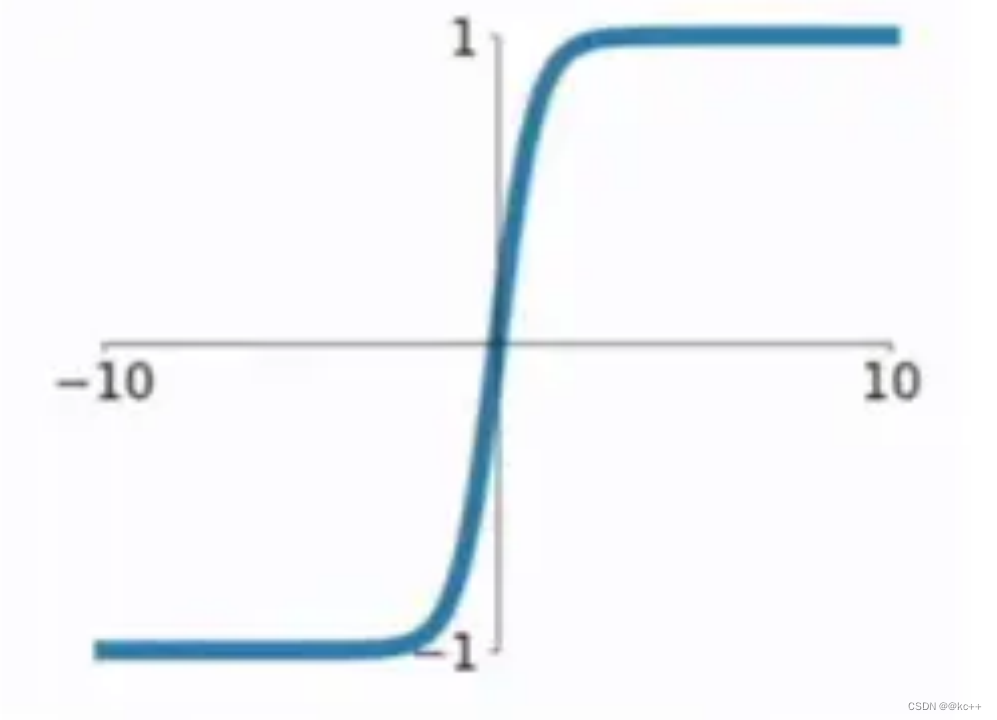
print(sigmoid(z))

6.2 激活函数-tanh

以0为均值，解决了sigmoid的一定缺点，但是依然存在梯度消失问题计算同样非常耗时

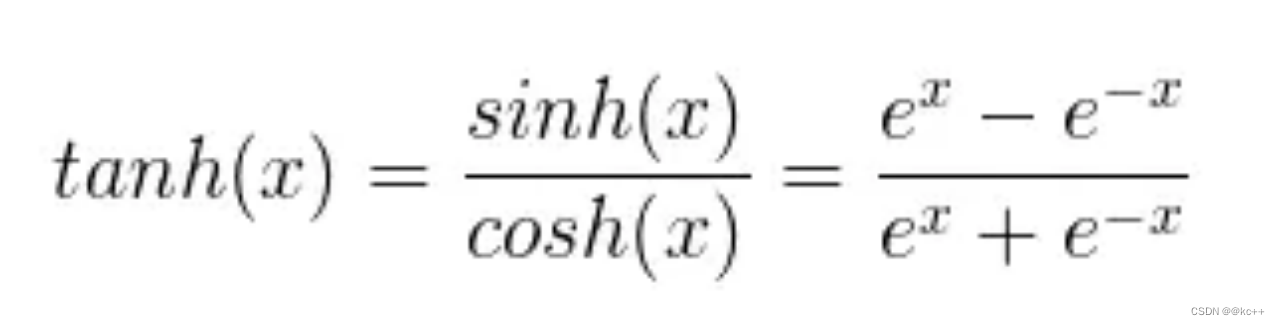
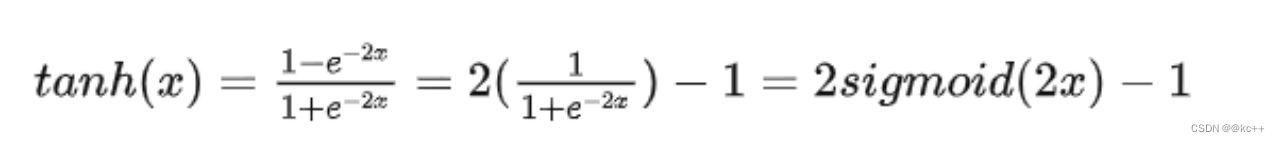
import numpy as npdef tanh(z):return np.tanh(z)# 示例
z = np.array([-1.0, 0.0, 1.0])
print(tanh(z))

6.3 激活函数-Relu

在正区间不易发生梯度消失
计算速度非常快
一定程度上降低过拟合的风险

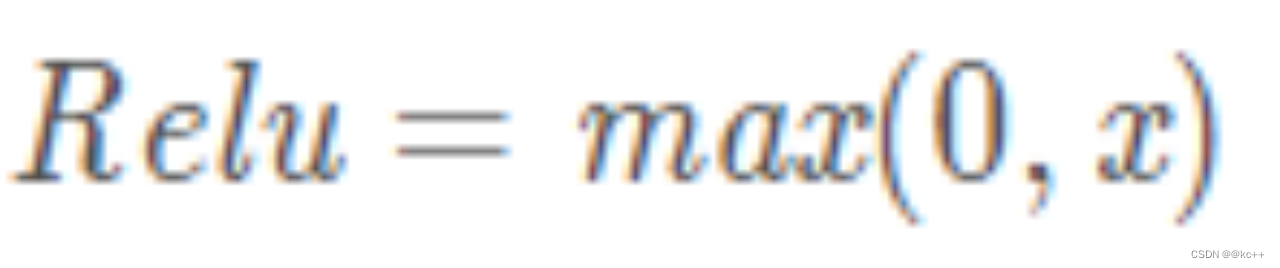
import numpy as npdef relu(z):return np.maximum(0, z)# 示例
z = np.array([-1.0, 0.0, 1.0])
print(relu(z))

6.4 激活函数-Softmax

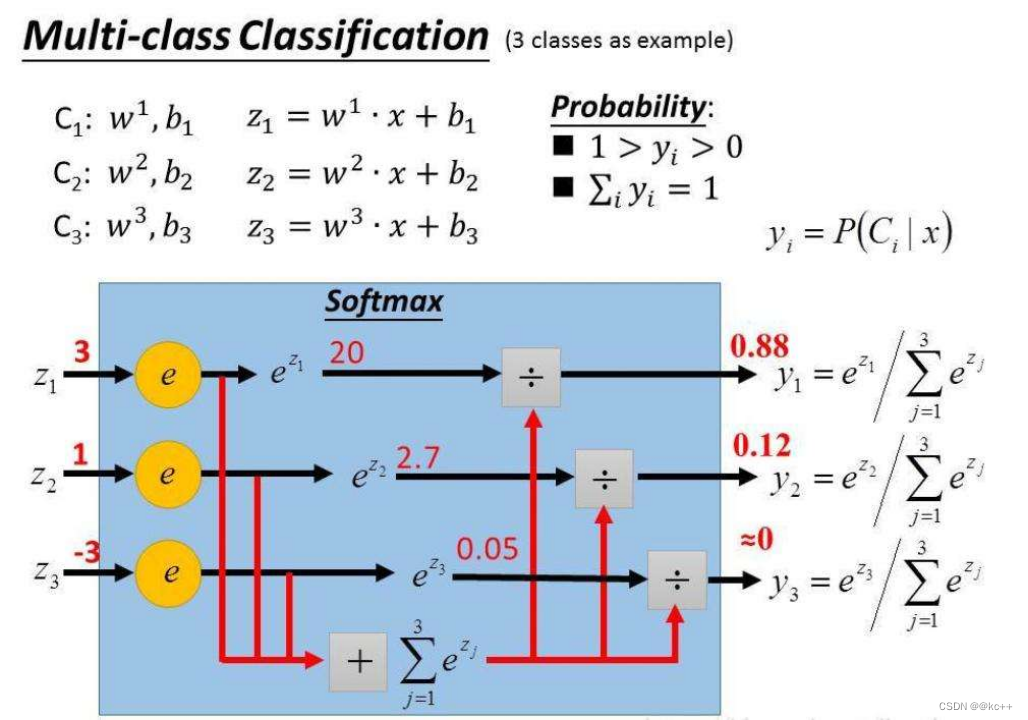
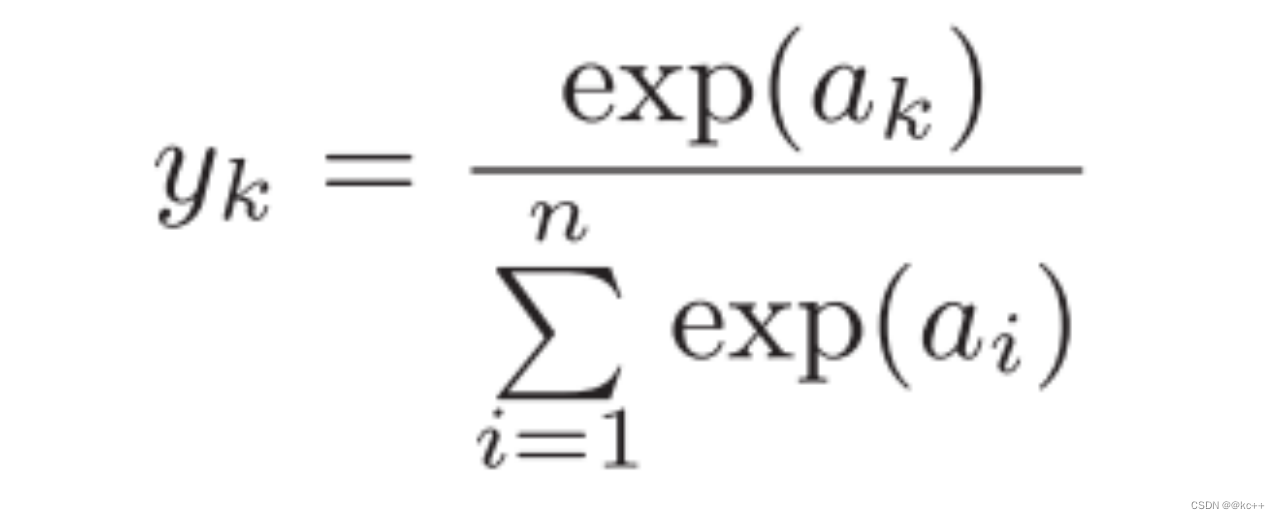
代码示例

#coding:utf8
import torch
import numpy'''
softmax的计算
'''def softmax(x):res = []for i in x:res.append(numpy.exp(i))res = [r / sum(res) for r in res]return res#e的1次方
print(numpy.exp(1))x = [1,2,3,4]
#torch实现的softmax
print(torch.softmax(torch.Tensor(x), 0))
#自己实现的softmax
print(softmax(x))

7. 损失函数

损失函数（也称为代价函数或误差函数）是一个核心组件于许多机器学习、统计学和优化任务中。它用于描述模型预测值与真实值之间的差异。通过最小化损失函数，我们可以找到模型的最佳参数，使模型的预测更加接近实际值。

7.1 损失函数-均方差

MSE mean square error
对均方差在做开根号，可以得到根方差

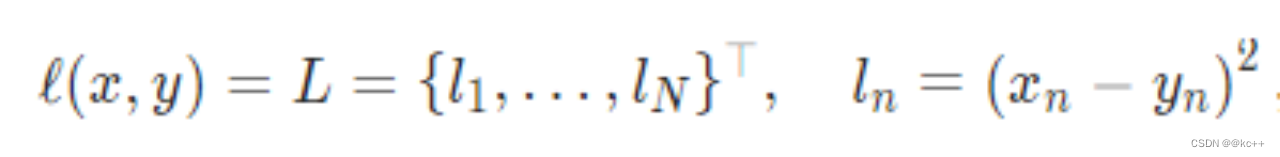
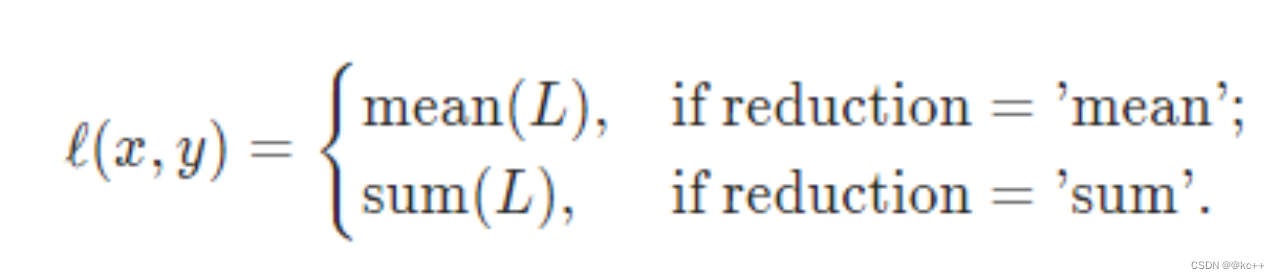
import numpy as npdef mean_squared_error(y_true, y_pred):return ((y_true - y_pred) ** 2).mean()# 示例
y_true = np.array([2.0, 4.0, 6.0])
y_pred = np.array([2.5, 3.5, 5.5])
print(mean_squared_error(y_true, y_pred))

7.2 损失函数-交叉熵

Cross Entropy
常用于分类任务
分类任务中，网络输出经常是所有类别上的概率分布
公式：

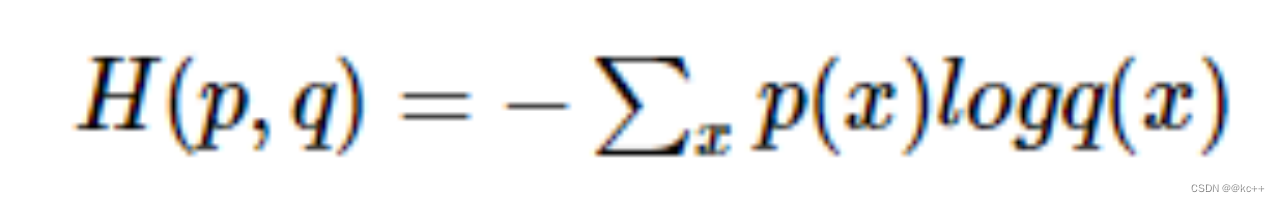
假设一个三分类任务，某样本的正确标签是第一类，则p = [1, 0, 0], 模型预测值假设为[0.5, 0.4, 0.1], 则交叉熵计算如下：

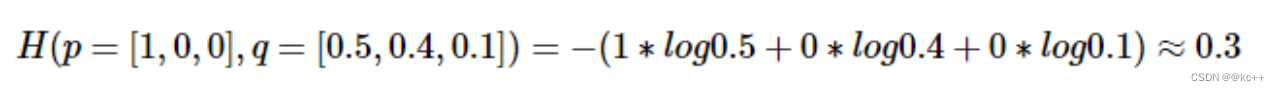
代码示例

import torch
import torch.nn as nn
import numpy as np'''
手动实现交叉熵的计算
'''#使用torch计算交叉熵
ce_loss = nn.CrossEntropyLoss()
#假设有3个样本，每个都在做3分类
pred = torch.FloatTensor([[0.3, 0.1, 0.3],[0.9, 0.2, 0.9],[0.5, 0.4, 0.2]])
#正确的类别分别为1,2,0
target = torch.LongTensor([1, 2, 0])
loss = ce_loss(pred, target)
print(loss, "torch输出交叉熵")#实现softmax函数
def softmax(matrix):return np.exp(matrix) / np.sum(np.exp(matrix), axis=1, keepdims=True)#验证softmax函数
# print(torch.softmax(pred, dim=1))
# print(softmax(pred.numpy()))#将输入转化为onehot矩阵
def to_one_hot(target, shape):one_hot_target = np.zeros(shape)for i, t in enumerate(target):one_hot_target[i][t] = 1return one_hot_target#手动实现交叉熵
def cross_entropy(pred, target):batch_size, class_num = pred.shapepred = softmax(pred)target = to_one_hot(target, pred.shape)entropy = - np.sum(target * np.log(pred), axis=1)return sum(entropy) / batch_sizeprint(cross_entropy(pred.numpy(), target.numpy()), "手动实现交叉熵")

7.3 损失函数-其他

指数损失

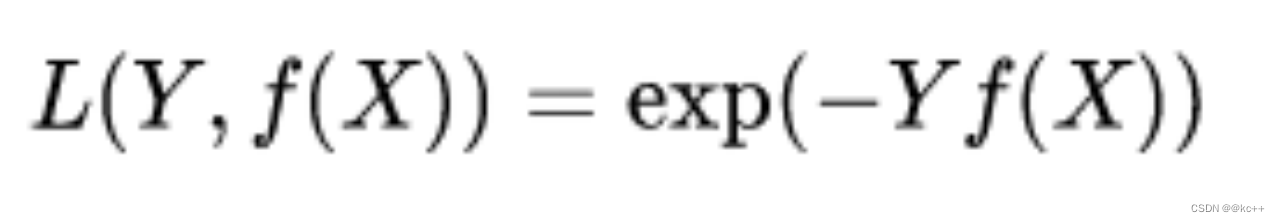
对数损失

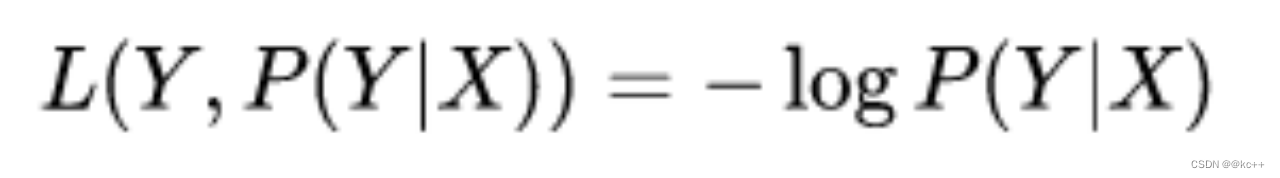
0/1损失

Hinge损失（二分类）

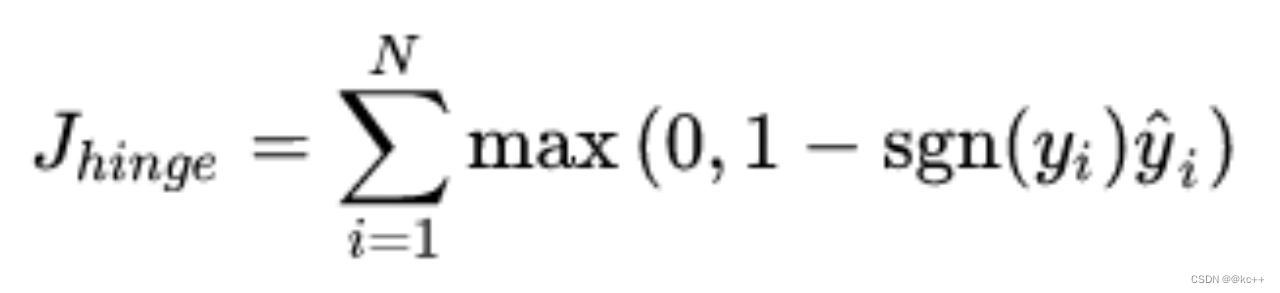
8. 优化器

优化器-Adam

1. 实现简单，计算高效，对内存需求少
2. 超参数具有很好的解释性，且通常无需调整或仅需很少的微调
3. 更新的步长能够被限制在大致的范围内（初始学习率）
4. 能够表现出自动调整学习率
5. 很适合应用于大规模的数据及参数的场景
6. 适用于不稳定目标函数
7. 适用于梯度稀疏或梯度存在很大噪声的问题

9. Pytorch

代码示例

# coding:utf8import torch
import torch.nn as nn
import numpy as np
import random
import json
import matplotlib.pyplot as plt"""基于pytorch框架编写模型训练
实现一个自行构造的找规律(机器学习)任务
规律：x是一个5维向量，如果第1个数>第5个数，则为正样本，反之为负样本"""class TorchModel(nn.Module):def __init__(self, input_size):super(TorchModel, self).__init__()self.linear = nn.Linear(input_size, 1)  # 线性层self.activation = torch.sigmoid  # sigmoid归一化函数self.loss = nn.functional.mse_loss  # loss函数采用均方差损失# 当输入真实标签，返回loss值；无真实标签，返回预测值def forward(self, x, y=None):x = self.linear(x)  # (batch_size, input_size) -> (batch_size, 1)y_pred = self.activation(x)  # (batch_size, 1) -> (batch_size, 1)if y is not None:return self.loss(y_pred, y)  # 预测值和真实值计算损失else:return y_pred  # 输出预测结果# 生成一个样本, 样本的生成方法，代表了我们要学习的规律
# 随机生成一个5维向量，如果第一个值大于第五个值，认为是正样本，反之为负样本
def build_sample():x = np.random.random(5)if x[0] > x[4]:return x, 1else:return x, 0# 随机生成一批样本
# 正负样本均匀生成
def build_dataset(total_sample_num):X = []Y = []for i in range(total_sample_num):x, y = build_sample()X.append(x)Y.append([y])return torch.FloatTensor(X), torch.FloatTensor(Y)# 测试代码
# 用来测试每轮模型的准确率
def evaluate(model):model.eval()test_sample_num = 100x, y = build_dataset(test_sample_num)print("本次预测集中共有%d个正样本，%d个负样本" % (sum(y), test_sample_num - sum(y)))correct, wrong = 0, 0with torch.no_grad():y_pred = model(x)  # 模型预测for y_p, y_t in zip(y_pred, y):  # 与真实标签进行对比if float(y_p) < 0.5 and int(y_t) == 0:correct += 1  # 负样本判断正确elif float(y_p) >= 0.5 and int(y_t) == 1:correct += 1  # 正样本判断正确else:wrong += 1print("正确预测个数：%d, 正确率：%f" % (correct, correct / (correct + wrong)))return correct / (correct + wrong)def main():# 配置参数epoch_num = 10  # 训练轮数batch_size = 20  # 每次训练样本个数train_sample = 5000  # 每轮训练总共训练的样本总数input_size = 5  # 输入向量维度learning_rate = 0.001  # 学习率# 建立模型model = TorchModel(input_size)# 选择优化器optim = torch.optim.Adam(model.parameters(), lr=learning_rate)log = []# 创建训练集，正常任务是读取训练集train_x, train_y = build_dataset(train_sample)# 训练过程for epoch in range(epoch_num):model.train()watch_loss = []for batch_index in range(train_sample // batch_size):x = train_x[batch_index * batch_size : (batch_index + 1) * batch_size]y = train_y[batch_index * batch_size : (batch_index + 1) * batch_size]optim.zero_grad()  # 梯度归零loss = model(x, y)  # 计算lossloss.backward()  # 计算梯度optim.step()  # 更新权重watch_loss.append(loss.item())print("=========\n第%d轮平均loss:%f" % (epoch + 1, np.mean(watch_loss)))acc = evaluate(model)  # 测试本轮模型结果log.append([acc, float(np.mean(watch_loss))])# 保存模型torch.save(model.state_dict(), "model.pth")# 画图print(log)plt.plot(range(len(log)), [l[0] for l in log], label="acc")  # 画acc曲线plt.plot(range(len(log)), [l[1] for l in log], label="loss")  # 画loss曲线plt.legend()plt.show()return# 使用训练好的模型做预测
def predict(model_path, input_vec):input_size = 5model = TorchModel(input_size)model.load_state_dict(torch.load(model_path))  # 加载训练好的权重# print(model.state_dict())model.eval()  # 测试模式with torch.no_grad():  # 不计算梯度result = model.forward(torch.FloatTensor(input_vec))  # 模型预测for vec, res in zip(input_vec, result):print("输入：%s, 预测类别：%d, 概率值：%f" % (vec, round(float(res)), res))  # 打印结果if __name__ == "__main__":main()test_vec = [[0.47889086,0.15229675,0.31082123,0.03504317,0.18920843],[0.94963533,0.5524256,0.95758807,0.95520434,0.84890681],[0.78797868,0.67482528,0.13625847,0.34675372,0.99871392],[0.1349776,0.59416669,0.92579291,0.41567412,0.7358894]]predict("model.pth", test_vec)