1. 求函数最优值
1.1求一元函数的最小值
如果给定了一个一元数学函数,可以使用 fminbnd 函数求该函数在给定区间中的局部最小值。例如,请考虑 MATLAB® 提供的 humps.m 函数。下图显示了 humps 的图。
x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel('x')
ylabel('humps(x)')
grid on
若要计算 humps 函数在 (0.3,1) 范围内的最小值,请使用
x = fminbnd(@humps,0.3,1) x = 0.6370
您可以通过使用 optimset 创建选项并将 Display 选项设置为 'iter' 来查看求解过程的详细信息。将所得选项传递给 fminbnd 。
options = optimset('Display','iter');
x = fminbnd(@humps,0.3,1,options) Func-count x f(x) Procedure
1 0.567376 12.9098 initial
2 0.732624 13.7746 golden
3 0.465248 25.1714 golden
4 0.644416 11.2693 parabolic
5 0.6413 11.2583 parabolic
6 0.637618 11.2529 parabolic
7 0.636985 11.2528 parabolic
8 0.637019 11.2528 parabolic
9 0.637052 11.2528 parabolic
Optimization terminated:
the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04
x = 0.6370
这种迭代输出显示了 x 的当前值以及每次计算函数时 f(x) 处的函数值。对于 fminbnd,一次函数计算对应一次算法迭代。最后一列显示 fminbnd 在每次迭代中使用的过程,即黄金分割搜索或抛物线插值。。
1.2 求多元函数的最小值
fminsearch 函数与 fminbnd 类似,不同之处在于前者处理多变量函数。请指定起始向量 x 0,而非起始区间。 fminsearch 尝试返回一个向量 x,该向量是数学函数在此起始向量附近的局部最小值。要尝试执行 fminsearch ,请创建一个三元(即 x 、 y 和 z )函数 three_var 。
function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2; 现在,使用 x = -0.6 、 y = -1.2 和 z = 0.135 作为起始值求此函数的最小值。
v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v) a =
0.0000 -1.5708 0.1803
1.3 求函数最大值
fminbnd 和 fminsearch 求解器尝试求目标函数的最小值。如果您有最大化问题,即以下形式的问题:

然后定义 g(x) = –f(x),并对 g 取最小值。
例如,要计算 tan(cos(x)) 在 x = 5 附近的最大值,请计算:
[x fval] = fminbnd(@(x)-tan(cos(x)),3,8) x =
6.2832
fval =
-1.5574
最大值为 1.5574(报告的 fval 的负值),并出现在 x = 6.2832。此答案是正确的,因为最大值为 tan(1)= 1.5574(最多五位数),该值出现在 x = 2π = 6.2832 位置。
1.4 fminsearch 算法
fminsearch 使用 Lagarias 等人的著作 [1] 中所述的 Nelder-Mead 单纯形算法。此算法对 n 维向量 x 使用 n + 1 个点组成的单纯形。此算法首先向 x 0 添加各分量 x 0 (i) 的 5%,以围绕初始估计值 x 0 生成一个单纯形。然后,该算法使用上述 n 个向量作为单纯形的除 x 0 之外的元素。(如果 x0 (i) = 0,则算法使用0.00025 作为分量 i)。然后,此算法按照以下过程反复修改单纯形。 注意 fminsearch 迭代输出方式中的关键字在相应的步骤说明后以 粗体 形式显示。
步骤1 用 x(i) 表示当前单纯形中的点列表 i = 1,...,n + 1。
步骤2 按最小函数值 f(x(1)) 到最大函数值 f(x(n + 1)) 的顺序对单纯形中的点进行排序。在迭代的每个步骤 中,此算法都会放弃当前的最差点 x(n + 1) 并接受单纯形中的另一个点。[或者在下面的步骤 7 中,此算法会更改值在 f(x(1)) 上方的所有 n 个点。]
步骤3 生成反射点
r = 2m – x(n + 1), (9-1)
其中
m = Σx(i)/n, i = 1...n, (9-2)
并计算 f(r)。
步骤4 如果 f(x(1)) ≤ f(r) < f(x(n)),则接受 r 并终止此迭代。 反射
步骤5 如果 f(r) < f(x(1)),则计算延伸点 s
s = m + 2(m – x(n + 1)), (9-3)
并计算 f(s)。
a 如果 f(s) < f(r),接受 s 并终止迭代。 扩展
b 否则,接受 r 并终止迭代。 反射
步骤6 如果 f(r) ≥ f(x(n)),则在 m 和 x(n + 1) 或 r(取目标函数值较低者)之间执行收缩。
a 如果 f(r) < f(x(n + 1))(即 r 优于 x(n + 1)),则计算
c = m + (r – m)/2 (9-4)
并计算 f(c)。如果 f(c) < f(r),则接受 c 并终止迭代。 外收缩
否则,继续执行步骤 7(收缩)。
b 如果 f(r) ≥ f(x(n + 1)),则计算
cc = m + (x(n + 1) – m)/2 (9-5)
并计算 f(cc)。如果 f(cc) < f(x(n + 1)),则接受 cc 并终止迭代。内收缩
否则,继续执行步骤 7(收缩)。
步骤7 计算 n 点
v(i) = x(1) + (x(i) – x(1))/2 (9-6)
并计算 f(v(i)),i = 2,...,n + 1。下一迭代中的单纯形为 x(1), v(2),...,v(n + 1)。收缩
下图显示了 fminsearch 可在此过程中计算的点以及每种可能的新单纯形。原始单纯形采用粗体边框。迭代将在符合停止条件之前继续运行。

2.非线性函数的数据拟合
此示例说明如何使用非线性函数对数据进行拟合。在本示例中,非线性函数是标准指数衰减曲线
y ( t ) = A exp( − λt ),
其中,y ( t ) 是时间 t 时的响应, A 和 λ 是要拟合的参数。对曲线进行拟合是指找出能够使误差平方和最小化的参数 A 和 λ
∑(i=1→n) [y i − A exp( − λt i )]^ 2 ,
其中,时间为 t i ,响应为 y i , i = 1, …, n 。误差平方和为目标函数。
2.1 创建样本数据
通常,您要通过测量获得数据。在此示例中,请基于 A = 40 和 λ = 0 . 5 且带正态分布伪随机误差的模型创建人工数据。
rng default % for reproducibility
tdata = 0:0.1:10;
ydata = 40*exp(-0.5*tdata) + randn(size(tdata));2.2 编写目标函数
编写一个函数,该函数可接受参数 A 和 lambda 以及数据 tdata 和 ydata ,并返回模型 y ( t ) 的误差平方和。将要优化的所有变量( A 和 lambda )置入单个向量变量 ( x)。
type sseval function sse = sseval(x,tdata,ydata)
A = x(1);
lambda = x(2);
sse = sum((ydata - A*exp(-lambda*tdata)).^2);
将此目标函数保存为 MATLAB® 路径上名为 sseval.m 的文件。fminsearch 求解器适用于一个变量 x 的函数。但 sseval 函数包含三个变量。额外变量 tdata 和 ydata 不是要优化的变量,而是用于优化的数据。将 fminsearch 的目标函数定义为仅含有一个变量 x 的函数:
fun = @(x)sseval(x,tdata,ydata); 有关包括额外参数(例如 tdata 和 ydata )的信息,请参阅“参数化函数” 。
2.3 求最优拟合参数
从随机正参数集 x0 开始,使用 fminsearch 求使得目标函数值最小的参数。
x0 = rand(2,1);
bestx = fminsearch(fun,x0) bestx = 2×1
40.6877
0.4984
结果 bestx 与生成数据的参数 A = 40 和 lambda = 0.5 相当接近。
2.4 检查拟合质量
要检查拟合质量,请绘制数据和生成的拟合响应曲线。根据返回的模型参数创建响应曲线。
A = bestx(1);
lambda = bestx(2);
yfit = A*exp(-lambda*tdata);
plot(tdata,ydata,'*');
hold on
plot(tdata,yfit,'r');
xlabel('tdata')
ylabel('Response Data and Curve')
title('Data and Best Fitting Exponential Curve')
legend('Data','Fitted Curve')
hold off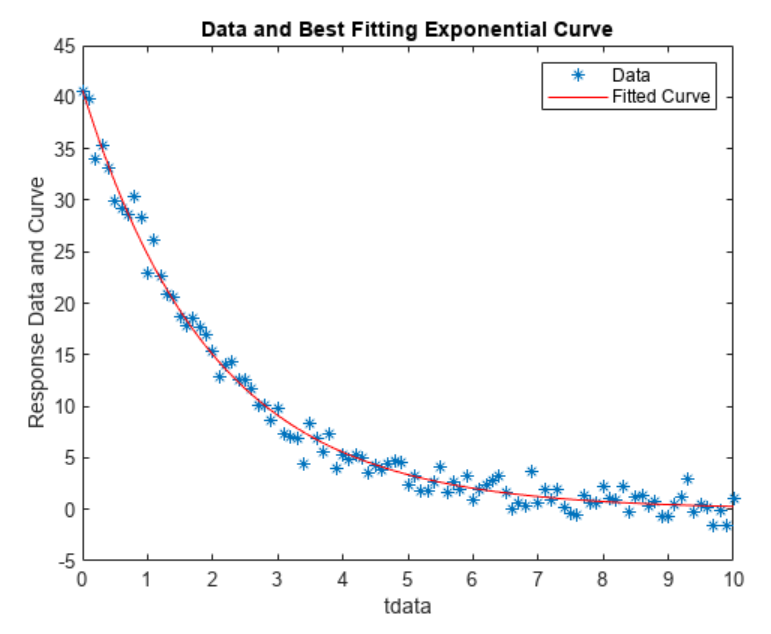





![[LeetCode111双周赛LeetCode359周赛] DP双指针](https://img-blog.csdnimg.cn/c17d9f8164d4447f87a5288aa724b9dd.png)


![java八股文面试[数据结构]——ArrayList和LinkedList区别](https://img-blog.csdnimg.cn/8d2841c06cf74e17b71e62919779f046.png)