树
无论是符号表还是线性表,随着元素的增多,增删查操作耗时增加,为了提高运算效率,需要树。
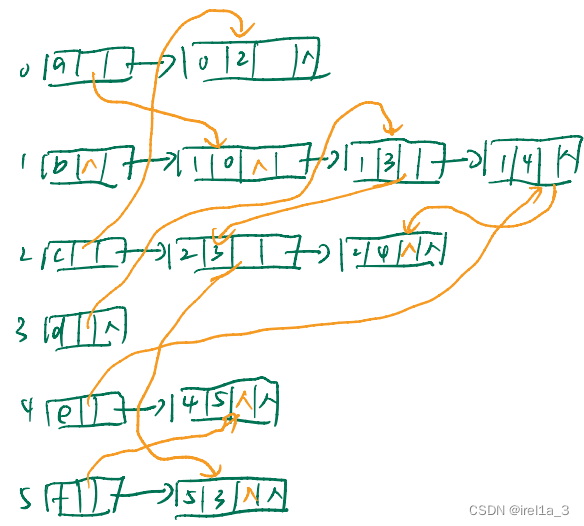
树是由N(N>=1)个有限结点组成一个具有层次关系的集合。
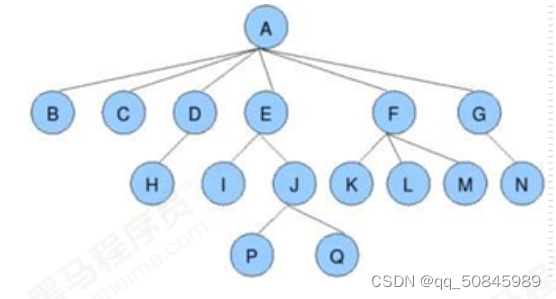
特征:
1.每个结点有零个或多个结点
2.没有父结点的结点为根节点
3.每个非根结点只有一个父结点
术语:
1.结点的度:一个结点含有的子树的个数。
2.叶结点:度为0的结点。
3.分支结点:度不为0的结点。
4.结点的层次:从根节点开始,根结点的层次为1,根的后继层次为2.
5.结点的层序编号:将树中的结点,按照上层到下层,同层从左到右的次序排成一个线性序列,变成自然数。
6.树的度:树中所有结点的度的最大值。
7.树的高度:树中结点的最大层次。
8.树林:m个互不相交的树的集合,将一个非空树的根节点删除,树就变成了一个森林。给森林增加一个统一的根结点,森林就变成了一棵树。

9.孩子结点:一个结点的直接后继结点。
10.双亲结点:一个结点的直接前驱结点。
11.兄弟结点:同一双亲结点的孩子结点。
二叉树
二叉树:度不超过2的树(每个结点最多有两个子结点)。
满二叉树:一个二叉树,每层的结点树都达到最大值。
完全二叉树:叶结点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层左侧位置。

private class Node<Key,Value>{
//存储键
public Key key;
//存储值
private Value value;
//记录左子结点
public Node left;
//记录右子结点
public Node right;
public Node(Key key, Value value, Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}二叉树插入:
插入方法put实现思想:
1.如果当前树中没有任何一个结点,则直接把新结点当做根结点使用
2.如果当前树不为空,则从根结点开始:
2.1如果新结点的key小于当前结点的key,则继续找当前结点的左子结点;
2.2如果新结点的key大于当前结点的key,则继续找当前结点的右子结点;
2.3如果新结点的key等于当前结点的key,则树中已经存在这样的结点,替换该结点的value值即可。
//向指定的树x中添加key-value,并返回添加元素后新的树
private Node put(Node x, Key key, Value value) {
if (x == null) {
//个数+1
N++;
return new Node(key, value, null, null);
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//新结点的key大于当前结点的key,继续找当前结点的右子结点
x.right = put(x.right, key, value);
} else if (cmp < 0) {
//新结点的key小于当前结点的key,继续找当前结点的左子结点
x.left = put(x.left, key, value);
} else {
//新结点的key等于当前结点的key,把当前结点的value进行替换
x.value = value;
}
return x;
}查询方法get实现思想:
从根节点开始:
1.如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;
2.如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;
3.如果要查询的key等于当前结点的key,则树中返回当前结点的value。
public Value get(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;
return get(x.right, key);
} else if (cmp < 0) {
//如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;
return get(x.left, key);
} else {
//如果要查询的key等于当前结点的key,则树中返回当前结点的value。
return x.value;
}
}
删除方法delete实现思想:
1.找到被删除结点;
2.找到被删除结点右子树中的最小结点minNode
3.删除右子树中的最小结点
4.让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子
树
5.让被删除结点的父节点指向最小结点minNode
//删除指定树x中的key对应的value,并返回删除后的新树
public Node delete(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//新结点的key大于当前结点的key,继续找当前结点的右子结点
x.right = delete(x.right, key);
} else if (cmp < 0) {
//新结点的key小于当前结点的key,继续找当前结点的左子结点
x.left = delete(x.left, key);
} else {
//新结点的key等于当前结点的key,当前x就是要删除的结点
//1.如果当前结点的右子树不存在,则直接返回当前结点的左子结点
if (x.right == null) {
return x.left;
}
//2.如果当前结点的左子树不存在,则直接返回当前结点的右子结点
if (x.left == null) {
return x.right;
}
//3.当前结点的左右子树都存在
//3.1找到右子树中最小的结点
Node minNode = x.right;
while (minNode.left != null) {
minNode = minNode.left;
}
//3.2删除右子树中最小的结点
Node n = x.right;
while (n.left != null) {
if (n.left.left == null) {
n.left = null;
} else {
n = n.left;
}
}
//3.3让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点
minNode的右子树
minNode.left = x.left;
minNode.right = x.right;
//3.4让被删除结点的父节点指向最小结点minNode
x = minNode;
//个数-1
N--;
}
return x;
}二叉树遍历
前序遍历:先访问根节点,然后再访问左子树,最后访问右子树。
中序遍历:先访问左子树,再访问根节点,最后访问右子树。
后序遍历:先访问左子树,再访问右子树,最后访问根结点。
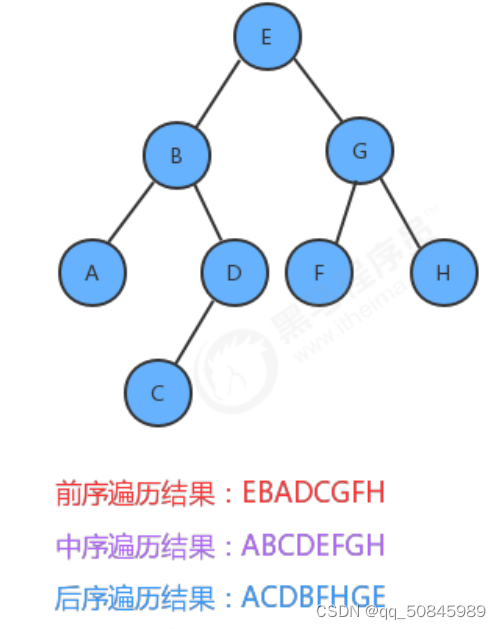
前序遍历思想:
1.把当前结点的key放入到队列中;
2.找到当前结点的左子树,如果不为空,递归遍历左子树
3.找到当前结点的右子树,如果不为空,递归遍历右子树
//使用前序遍历,把指定树x中的所有键放入到keys队列中
private void preErgodic(Node x,Queue<Key> keys){
if (x==null){
return;
}
//1.把当前结点的key放入到队列中;
keys.enqueue(x.key);
//2.找到当前结点的左子树,如果不为空,递归遍历左子树
if (x.left!=null){
preErgodic(x.left,keys);
}
//3.找到当前结点的右子树,如果不为空,递归遍历右子树
if (x.right!=null){
preErgodic(x.right,keys);
}
}