课程推荐: 13 非线性规划算法在数学建模中的应用与编程实现_哔哩哔哩_bilibili
一、非线性规划模型
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不像线性规划有单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。
1.1 案例
投资决策问题:
某企业有n个项目可供选择投资,并且至少要对其中一个项目投资。已知该企业拥有总资金A元,投资于第i, i = 1,2,…,n个项目需花资金
元,并预计可收益
元。试选择最佳投资方案。
Q:为什么说这个题目是非线性的呢?
A:限制条件指明至少要投资一个项目,因此目标函数不能仅考虑收益最大,还要考虑花资金最小。
设置决策变量:
则,投资总额为
,投资总收益为
。
限制条件:
模型:
1.2 非线性规划的数学模型
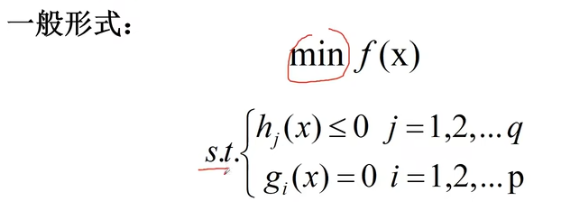
在一组等式或不等式的约束下,求一个函数的最大值(或最小值)问题,其中至少有一个非线性函数,这类问题称之为非线性规划问题。
非线性规划在mathlab中的标准格式:

非线性规划在mathlab中的命令:
[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x的返回值是决策向量x的取值,fval返回的是目标函数的取值,其中fun是目标函数需用m文件定义。
- x0是x的初始值。
- A,b,Aeq,beq定义了线性约束Ax≤b,Aeq-x=beq,如果没有线性约束,则A=[],b=[],Aeq=[],beq=[]。
- lb和ub是变量x的下界和上界,如果上界和下界没有约束,即x无下界也无上界,则lb=[],ub=[]。
- nonlcon是用M文件定义的非线性约束函数c(x),ceq(x)。
- options定义了优化参数,可以使用Matlab缺省的参数设置。