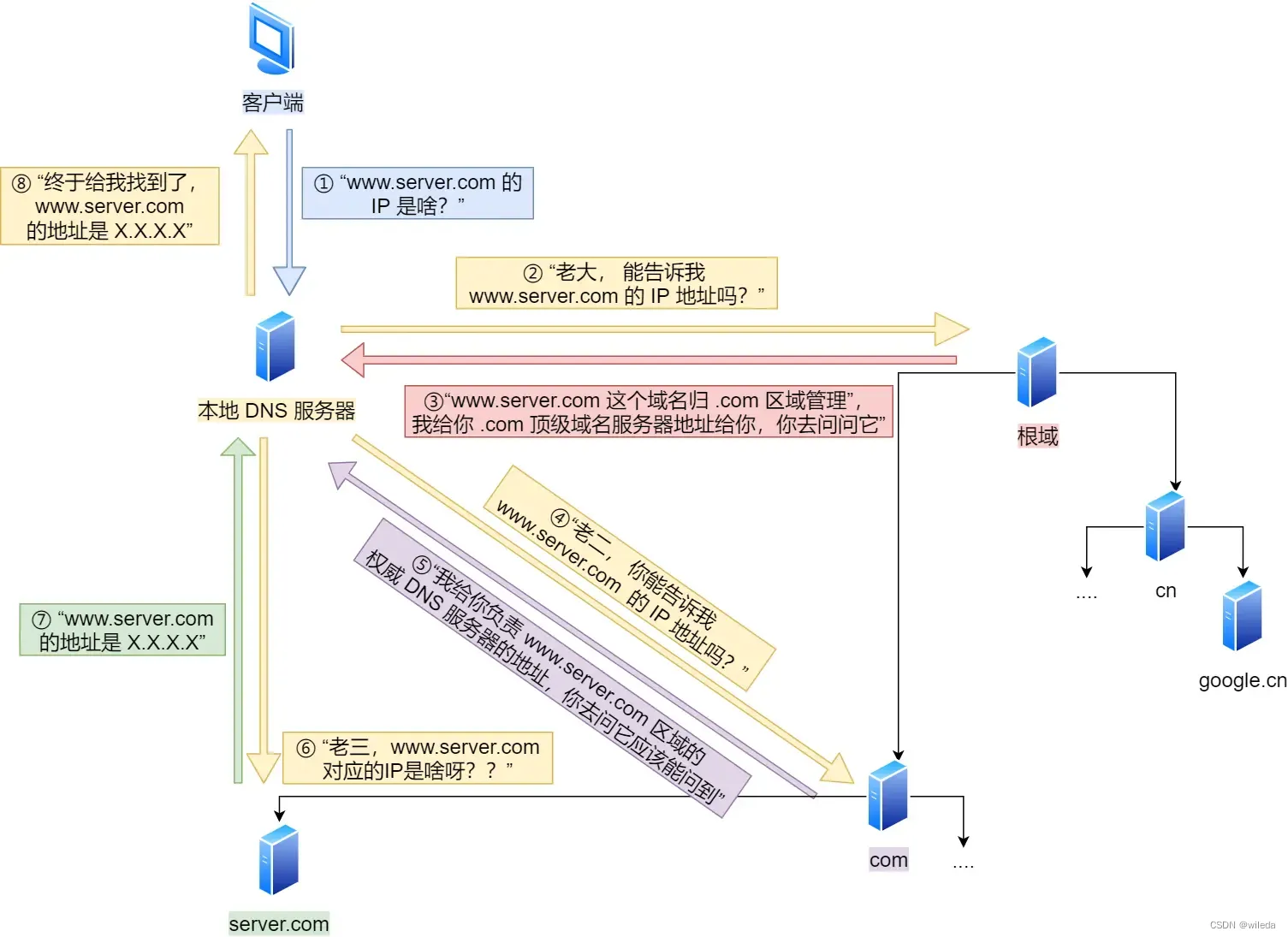
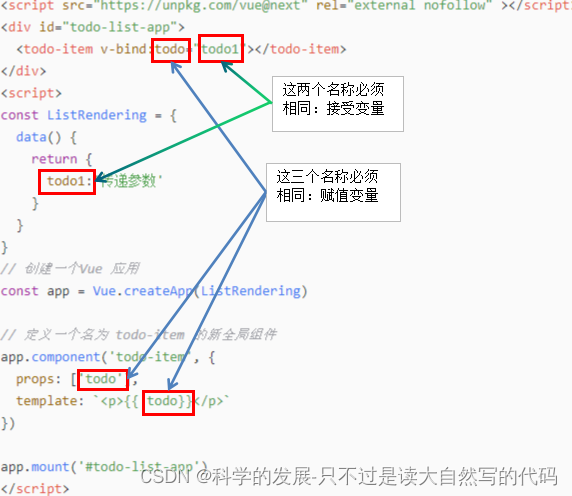
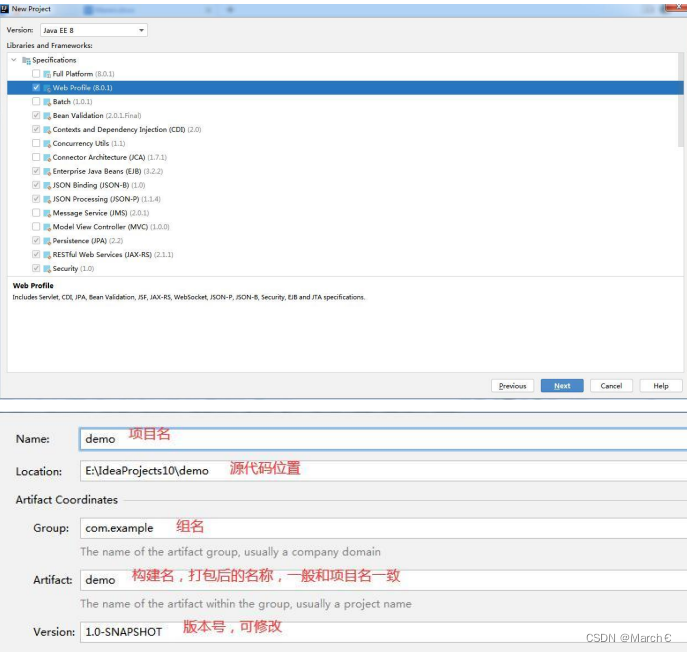
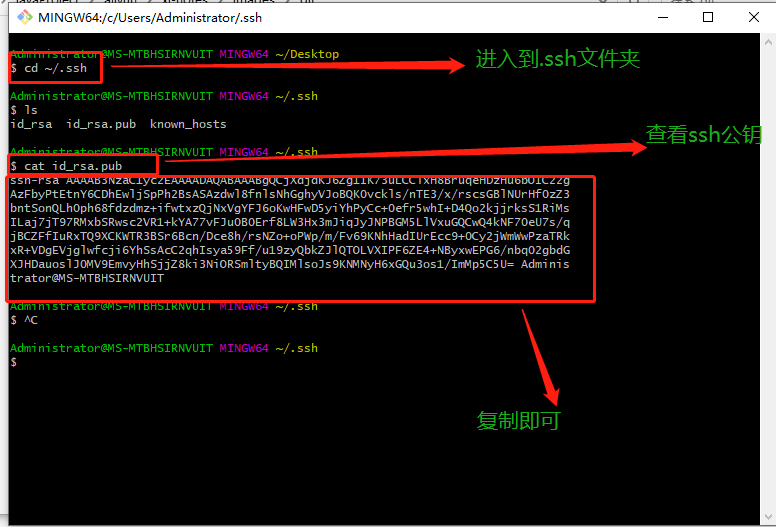
矩阵的乘法的映射图(不属于本文)
矩阵的乘法具有不可交换性
A*B != B*A
A左乘*B != A右乘*B
假设A!=0, B!=0, 但是可能存在 A*B=0
假设A!=0, 但是可能存在 A*A=0
如果已知 A*B=C,那么 B= A-*C ,但是B != C*A-
线性代数,矩阵,属于代数学,不属于几何学,
想理解矩阵乘法的几何意义有点难
3.3 特征值和特征向量是什么?
直接说现在:特征向量这个块往哪个方向进行了拉伸,各个方向拉伸了几倍。这也让人很容易理解为什么,行列式的值就是特征值的乘积。
特征向量也代表了一些良好的性质,即这些线在线性变换后没有发生方向的偏移(可以逆转)只是长度发生了改变。

4 线性代数的基本概念
为啥学数学?为啥学线代? - 知乎大问题:学数学有啥用?学线性代数有啥用? 小问题:专业、数学、计算机编程,该学哪个? 计算化学和其它计算xx一样,最重要的不是对编程语言的掌握,而是把一个化学问题构造成一个可计算的数学问题吧?这里面最重…https://zhuanlan.zhihu.com/p/586540676
一般的数学,研究数字之间的关系,有些数字用变量代替
而线性代数,研究数组--向量之间的关系 y=ax 其中 y,a,x都是数组,不只是a是数组
RGB颜色就是一种用数组来表达颜色的方式,而不是用数字
A,B两个同阶同秩N阵,看上去结构一样,但两厢相乘,在做在右,地位差别巨大。
在左,你就是基,是空间的根本,是坐标系,是往哪去、能到哪的定海神针,是如来佛手;在右,你就只是乾坤已定后数量的选择,你是翻十个跟头,还是翻十一个(都出不了如来佛掌不是)?无论右侧有多少变,折腾的结果都在左侧框定的空间里。
矩阵相乘,在左在右,意义不同 - 知乎补2(20220102) 一下原文只从代数的角度解释了矩阵在左在右的不同含义导致的矩阵乘法不可交换,本补从左右矩阵数组(列向量)的不同实体性质再来解释一下。 线代与函数的最大区别在于函数是研究数字之间的关系的,线…https://zhuanlan.zhihu.com/p/166080173矩阵乘法的本质是什么? - 知乎矩阵的乘法,本质是一种运动。我这里提供一个我认为具有启发性的模型,来阐述为什么矩阵乘法是运动。1 线…https://www.zhihu.com/question/21351965/answer/204058188


一直不解,为什么如此定义矩阵的乘法,为什么这样一种怪异的乘法规则却能够在实践中发挥如此巨大的功效? - 知乎大家讲了这么多有的没的,我给大家举个“矩阵”在现实世界中用到的例子:==============================…https://www.zhihu.com/question/30898332/answer/2687307391



先讲讲基与维数。一个线性空间必定存在基,线性空间的任意元素都可以由基线性表出,且表出方式唯一,这个唯一的表出的组合就是这个元素在这个基下的坐标。线性表出且表出方式唯一的充分必要条件是什么?这里又引出了线性无关以及极大线性无关组的概念,极大线性无关组元素的个数又能引出秩的概念。由秩又能引出维度的概念。以上这些概念都是为了刻画线性空间的基与维数而衍生出来的,并不是凭空出现无中生有的。
下面再谈谈同构。线性空间千千万,应如何研究呢?同构就是这样一个强大的概念,任何维数相同的线性空间之间是同构的,空间的维数是简单而深刻的,简单的自然数居然能够刻画空间最本质的性质。借助于同构,要研究任意一个n维线性空间,只要研究Rⁿ就行了。
n维线性空间作为一个整体,我们自然想到能不能先研究它的局部性质?所以自然而然的导出了子空间的概念以及整个空间的直和分解。直和分解要求把整个空间分解为两两不交的子空间之和,通过研究各个简单的子空间的性质,从而得出整个空间的性质。
4.2 线性映射
核空间
1)线性映射的核空间。这是线性映射的一个重要的概念,什么是线性映射的核空间呢?简单的说,就是映射到零的原像的集合,记作KER。用正比例函数来类比,显然当k不等于0时,它的核是零空间,当k为零时,它的核空间是整个R。
有时候需要判定一个线性映射是不是单射,按照定义来还是没那么好证的,这时我们可以从它的核来判定,只要它的核是零,那么这个线性映射必然是单射。
2)线性映射的像。当自变量取遍整个定义域时,它的像的取值范围成为一个线性子空间,称为像空间,记作IM。
3)线性映射的矩阵表示。一个抽象的线性映射应如何'解析'的表达出来呢?这个表达式写出来就是一个矩阵,且这个矩阵依赖于基的选择。也就是说在不同的基下,线性映射有不同的矩阵。基有无穷个,相应的矩阵有无穷个。这就给用矩阵研究线性映射带来了麻烦。
幸好我们有相似矩阵。同一个线性映射在不同的基下的矩阵是相似关系,相似不变量有秩,行列式,迹,特征值,特征多项式等。所以可以通过相似矩阵来研究线性映射的秩,行列式,迹,特征值,特征多项式等性质。
线性映射的矩阵有无穷多,那么这其中有哪些是值得关注的呢?第一就是标准正交基下的矩阵了,这也是最常见的。
然而一个线性映射的矩阵在标准正交基下可能特别复杂,所以需要选择一组特殊的基,让它的矩阵在这个基下有最简单的矩阵表示。如果存在这样的基,使得线性映射的矩阵为对角矩阵,则称这个线性映射可对角化。
然而是不是所有线性映射都可以对角化呢,遗憾的是,并不是。那么就要问,如果一个线性映射不能对角化,那么它的最简矩阵是什么?这个问题的答案是若尔当标准型。可以证明,在复数域上,任何线性映射都存在唯一的若尔当标准型。




网上推荐的线性代数的课程
- 一般推荐的都是国外的课程和书
- 首推这个mit的线性代数
麻省理工学院 - MIT - 线性代数(我愿称之为线性代数教程天花板)_哔哩哔哩_bilibili麻省理工学院 - MIT - 线性代数(我愿称之为线性代数教程天花板)共计35条视频,包括:1.01方程组的几何解释、2.02矩阵消元、3.03乘法和逆矩阵等,UP主更多精彩视频,请关注UP账号。https://www.bilibili.com/video/BV16Z4y1U7oU/?spm_id_from=333.337.search-card.all.click&vd_source=5fa6d2958ae880d9550a17f8050fd5ed
-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】_哔哩哔哩_bilibili-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】共计15条视频,包括:00-序言、01-向量究竟是什么、02-线性组合.张成的空间与基等,UP主更多精彩视频,请关注UP账号。https://www.bilibili.com/video/BV1ib411t7YR/?spm_id_from=333.337.search-card.all.click&vd_source=5fa6d2958ae880d9550a17f8050fd5ed
理解矩阵(一)——孟岩https://www.douban.com/note/779302982/?_i=07066238wuC-1A8分钟带你彻底弄懂《线性代数》 - 知乎这篇文章写得真好,解开了我的迷雾,另外,感觉想要真正理解线性代数,还是需要理解线性代数的几何意义 原文链接: https://mp.weixin.qq.com/s?__biz=MjM5NDQ0NjM5Mg==&mid=2650426885&idx=1&sn=a196…https://zhuanlan.zhihu.com/p/535053668線代啟示錄 | I seek not to know the answers, but to understand the questions.I seek not to know the answers, but to understand the questions.https://ccjou.wordpress.com/
线性代数的本质(转发) - 知乎线性代数的本质 在机器学习领域,线性代数无处不在,偶尔在网上看到这篇文章,觉得很好,就转过来了,希望能对大家有所启示。 线性代数课程,无论你从行列式入手还是直接从矩阵入手,从一开始就充斥着莫名其妙。 …https://zhuanlan.zhihu.com/p/362462011
1 线性代数和矩阵的各种概念
- 线性代数
- 向量
- 矩阵
- 行列数
- 什么是线性?什么是线性变化
- 等等
1.1 各种逻辑图
下图是网上找的思维导图。