169. 多数元素

难度：简单

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：

• n == nums.length
• 1 <= n <= 5 * 104
• -109 <= nums[i] <= 109

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。 

思路：采用两两相消的方法，因为多数元素出现的次数是大于n/2的，所以只要两两不相等的元素相消，剩下的那个元素就肯定是多数元素了

代码：

class Solution {public int majorityElement(int[] nums) {int more = nums[0];int count = 1;for(int i = 1; i < nums.length;i++ ){if(more == nums[i]) {count++;}else if(count == 0) {more = nums[i];count++;}else {count--;}}return more;}
}

运行结果：

 

189. 轮转数组

难度：中等

相关企业

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

• 1 <= nums.length <= 105
• -231 <= nums[i] <= 231 - 1
• 0 <= k <= 105

进阶：

• 尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
• 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

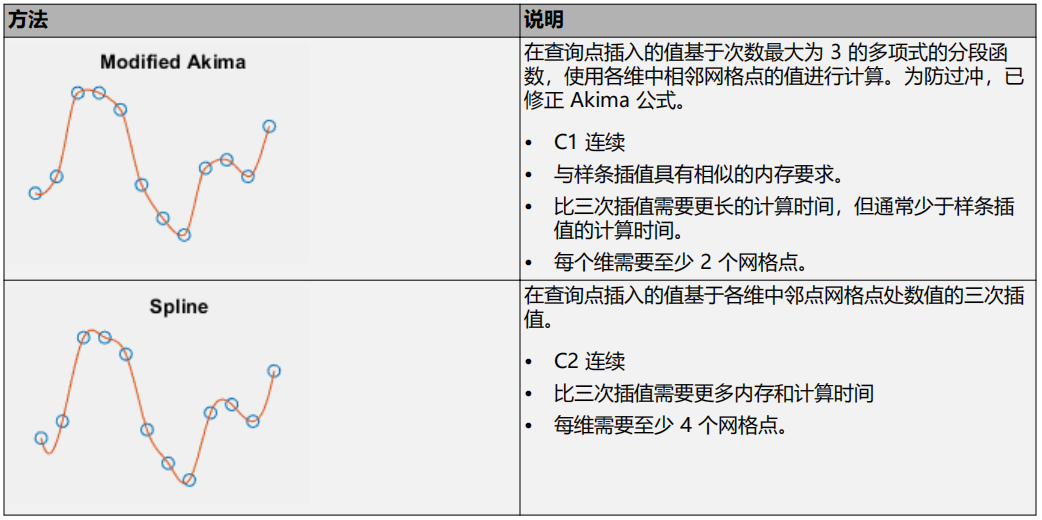
 思路：翻转三次，如图所示

 代码：

class Solution {public void reverse(int[] nums,int left,int right){       while(left < right){int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;left++;right--;}}public void rotate(int[] nums, int k) {int length = nums.length;k%=length;reverse(nums,0,length-1);reverse(nums,0,k-1);reverse(nums,k,length-1);}
}

运行结果：