【算法训练-链表】合并两个有序链表、合并K个有序链表

废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！首先，链表对应的数据结构在这篇Blog中：【基本数据结构一】线性数据结构：链表，基于对基础知识的理解来进行题目解答。本篇Blog的主题是合并有序链表，近半年考察还是比较多的
在这里插入图片描述

合并两个有序链表

先来个基础版，合并两个已排序的链表

题干

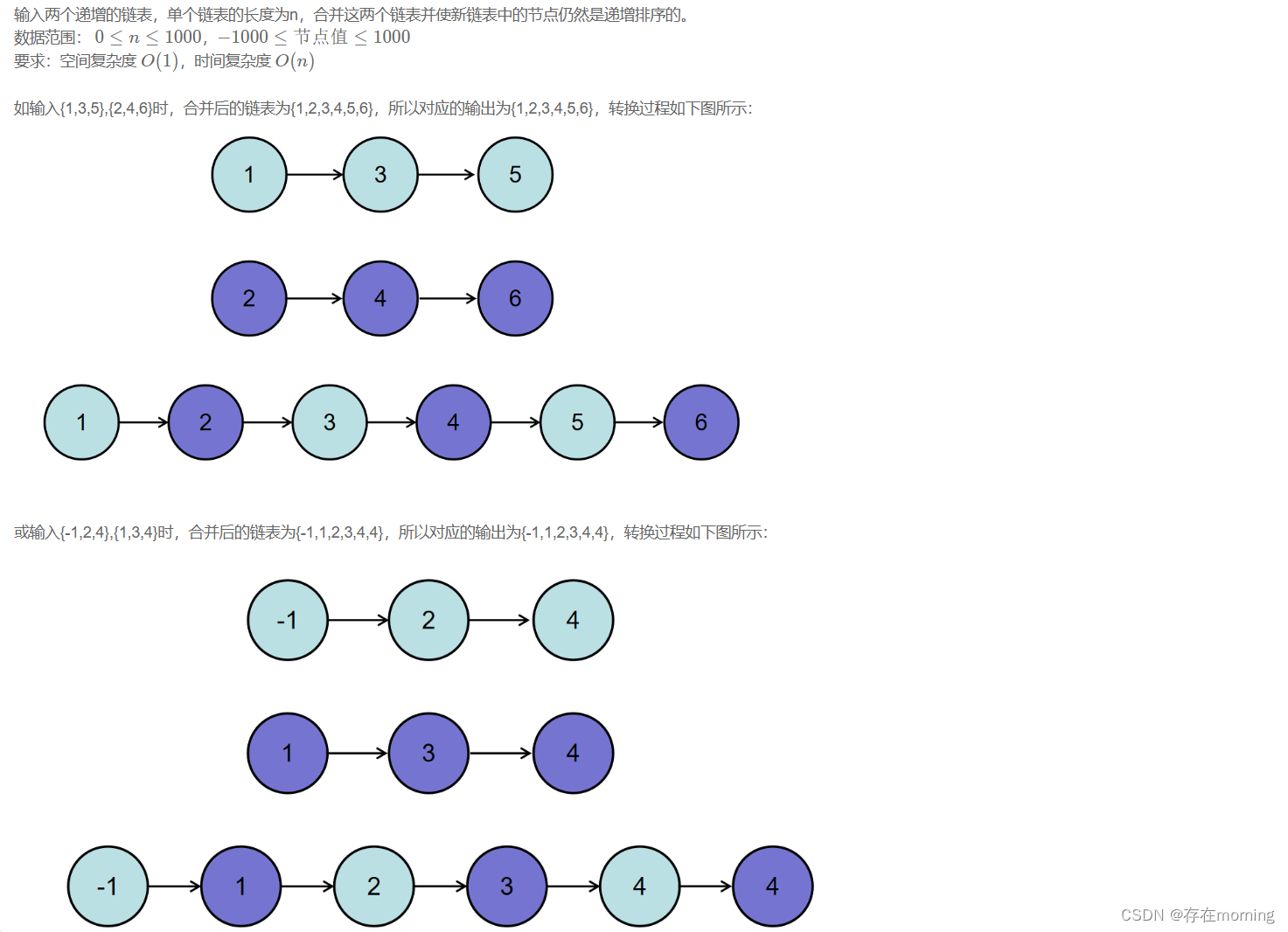
在这里插入图片描述

输入：
{1,3,5},{2,4,6}返回值：
{1,2,3,4,5,6}

输入：
{},{}返回值：
{}

输入：
{-1,2,4},{1,3,4}返回值：
{-1,1,2,3,4,4}

解题思路

整体目标就是在两个链表中选节点来构建新链表

设置result为哨兵结点，放置于新链表之前，最后返回的就是dummy.next；
设置cur为当前节点，从dummy开始，当两个链表都非空时进入循环，令新链表的下一个节点cur.next为val更小的节点，相应的链表节点后移一位，每次循环记得cur也要后移一位
如果循环结束后还有链表非空，cur指向非空链表，返回dummy.next

如下图所示：
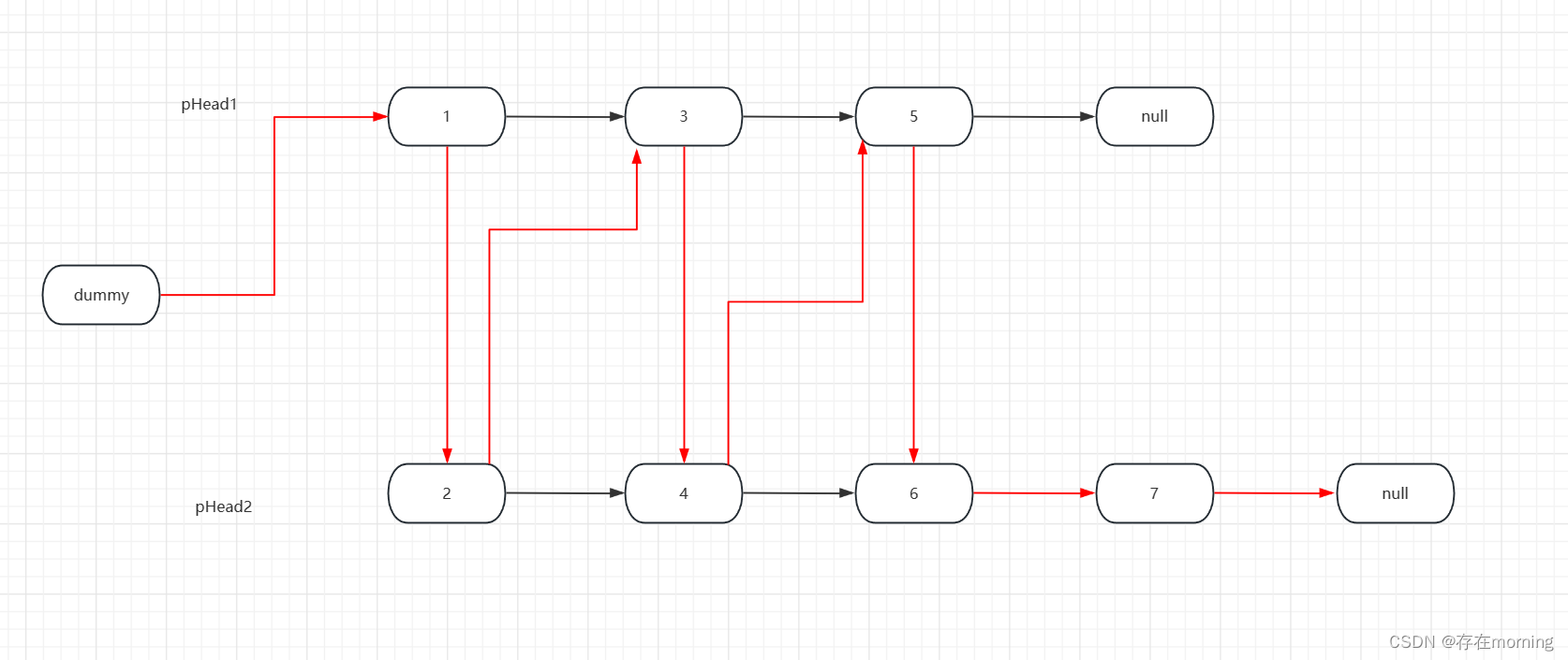
在这里插入图片描述

解题代码

Java实现

import java.util.*;/** public class ListNode {*   int val;*   ListNode next = null;*   public ListNode(int val) {*     this.val = val;*   }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param pHead1 ListNode类* @param pHead2 ListNode类* @return ListNode类*/public ListNode Merge (ListNode pHead1, ListNode pHead2) {// 1 如果其中一个为空列表，直接返回另一个if (pHead1 == null && pHead2 == null) {return null;}if (pHead1 == null) {return pHead2;}if (pHead2 == null) {return pHead1;}// 2 定义哨兵节点用来返回最终链表，cur用来检索两个链表的较小值节点ListNode dummy = new ListNode(-1);ListNode cur = dummy;while (pHead1 != null && pHead2 != null) {if (pHead1.val <= pHead2.val) {cur.next = pHead1;pHead1 = pHead1.next;} else {cur.next = pHead2;pHead2 = pHead2.next;}cur = cur.next;}// 3 一个链表空后，直接将另一个链表剩余部分拼接if (pHead1 == null) {cur.next = pHead2;}if (pHead2 == null) {cur.next = pHead1;}return dummy.next;}
}

时间复杂度O(N+M)：M N分别表示pHead1, pHead2的长度； 空间复杂度O(1)：常数级空间

合并K个有序链表

OK，难度升级，两个变成K个有序链表进行合并

题干

在这里插入图片描述

输入：
[{1,2,3},{4,5,6,7}]返回值：
{1,2,3,4,5,6,7}

输入：
[{1,2},{1,4,5},{6}]返回值：
{1,1,2,4,5,6}

解题思路

归并排序是什么？简单来说就是将一个数组每次划分成等长的两部分，对两部分进行排序即是子问题。对子问题继续划分，直到子问题只有1个元素。还原的时候呢，将每个子问题和它相邻的另一个子问题利用上述双指针的方式，1个与1个合并成2个，2个与2个合并成4个，因为这每个单独的子问题合并好的都是有序的，直到合并成原本长度的数组。

对于这k个链表，就相当于上述合并阶段的k个子问题，需要划分为链表数量更少的子问题，直到每一组合并时是两两合并，然后继续往上合并，这个过程基于递归：

终止条件：划分的时候直到左右区间相等或左边大于右边。
返回值：每级返回已经合并好的子问题链表。
本级任务：对半划分，将划分后的子问题合并成新的链表。

具体做法：

步骤一：从链表数组的首和尾开始，每次划分从中间开始划分，划分成两半，得到左边n/2个链表和右边n/2个链表
步骤二：继续不断递归划分，直到每部分链表数为1.
步骤三：将划分好的相邻两部分链表，按照两个有序链表合并的方式合并，合并好的两部分继续往上合并，直到最终合并成一个链表。

如下图所示，先进行合并链表划分
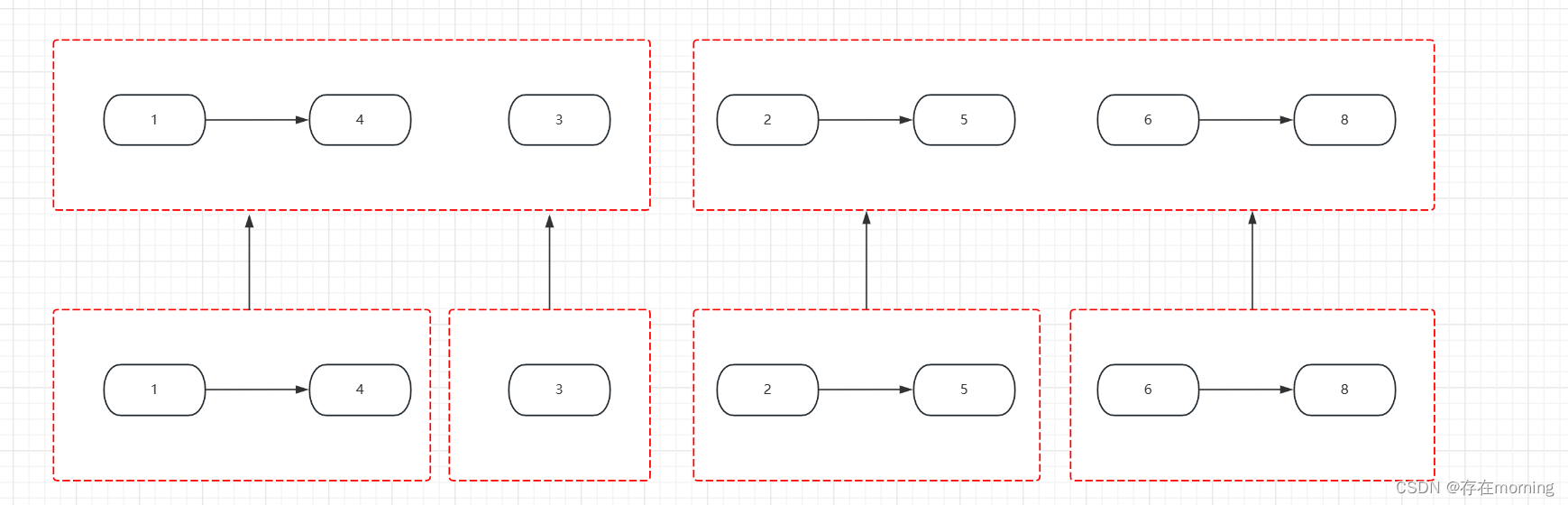
在这里插入图片描述
划分完子问题，子问题处理完返回到上一层级

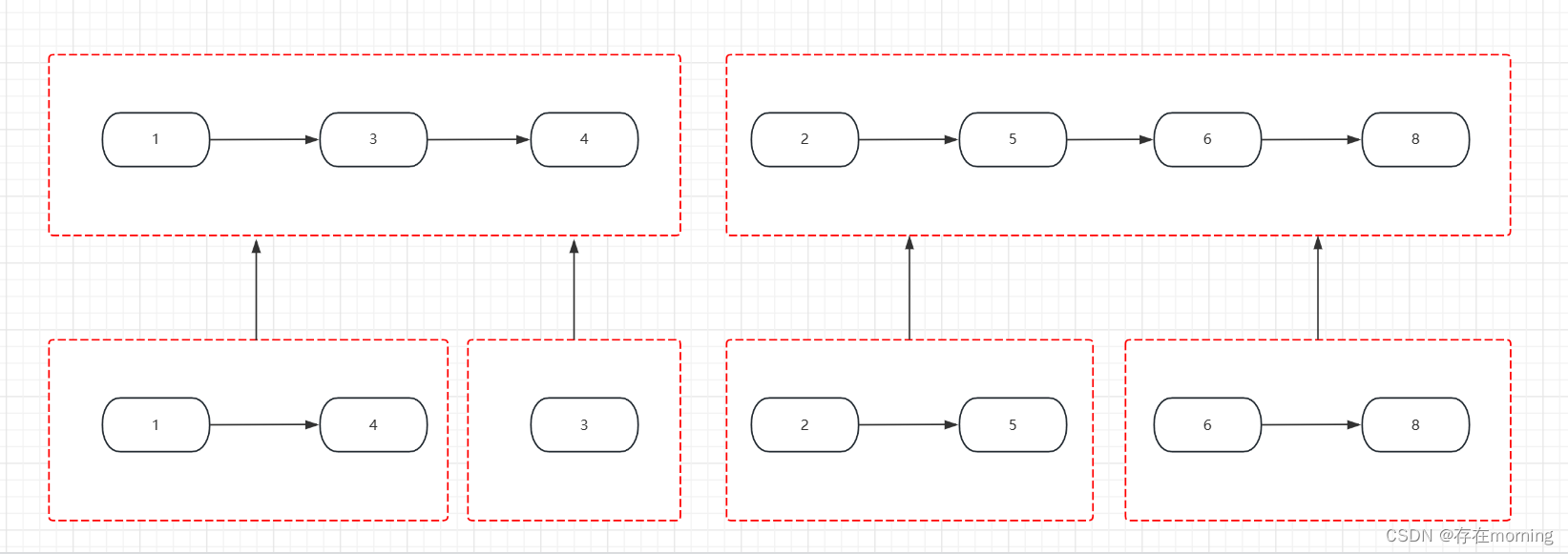
解题代码

Java实现代码

import java.util.*;/** public class ListNode {*   int val;*   ListNode next = null;*   public ListNode(int val) {*     this.val = val;*   }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param lists ListNode类ArrayList* @return ListNode类*/public ListNode mergeKLists (ArrayList<ListNode> lists) {return divideMerge(lists, 0, lists.size() - 1);}private ListNode divideMerge(ArrayList<ListNode> lists, int left, int right) {if (left > right) {return null;}// 终止条件，拿到了单独的链表if (left == right) {return lists.get(left);}int mid = (left + right) / 2;// 对两个相邻链表进行合并return merge(divideMerge(lists, left, mid), divideMerge(lists, mid + 1, right));}private ListNode merge(ListNode pHead1, ListNode pHead2) {// 1 链表非空判断if (pHead1 == null && pHead2 == null) {return null;}if (pHead1 == null) {return pHead2;}if (pHead2 == null) {return pHead1;}// 2 定义哨兵节点和最终返回链表ListNode dummy = new ListNode(-1);ListNode cur = dummy;while (pHead1 != null && pHead2 != null) {if (pHead1.val <= pHead2.val) {cur.next = pHead1;pHead1 = pHead1.next;} else {cur.next = pHead2;pHead2 = pHead2.next;}cur = cur.next;}// 3 如果一个链表空了，直接挂载另一个链表剩余节点if (pHead1 == null) {cur.next = pHead2;}if (pHead2 == null) {cur.next = pHead1;}return dummy.next;}
}

时间复杂度：O(nlogk)，其中n为所有链表的总节点数，分治为二叉树型递归，最坏情况下二叉树每层合并都是O(n)个节点，而分治次数为：O(logk)，所以总的时间复杂度就是O(nlogk)

空间复杂度：最坏情况下合并O(logk)，所以递归栈的深度为O(logk)

拓展：递归和分治的区别

递归（Recursion）和分治（Divide and Conquer）是两种解决问题的方法，它们有一些相似之处，但也存在一些关键的区别。

递归（Recursion）：
递归是一种问题解决方法，其中函数在其执行过程中调用自身来解决更小规模的子问题，直到达到基本情况，然后逐层返回结果以构建原始问题的解。递归的核心思想是将一个大问题划分为与原问题结构相同但规模更小的子问题，然后通过逐步解决这些子问题来解决原始问题。

分治（Divide and Conquer）：
分治是一种将问题分解为多个相互独立的子问题，然后解决这些子问题并将它们的解合并以得到原始问题解的方法。分治的核心思想是将一个大问题划分为多个独立的子问题，这些子问题可以并行地解决，然后将它们的解合并起来以得到原问题的解。

关键区别：

目标：
- 递归的目标是通过将问题分解为与原问题结构相同但规模更小的子问题，然后逐层解决这些子问题来得到原问题的解。
- 分治的目标是将问题分解为多个相互独立的子问题，然后并行地解决这些子问题，并将它们的解合并以得到原问题的解。
子问题之间的关系：
- 递归中，子问题之间的关系通常是相同结构的，但规模不同。
- 分治中，子问题通常是相互独立的，没有交叉。
解决方式：
- 递归解决问题时，通常需要考虑如何将问题分解为更小的子问题，然后将这些子问题的解组合起来。
- 分治解决问题时，通常需要考虑如何将问题分解为独立的子问题，然后并行地解决这些子问题，最后将它们的解合并起来。
合并过程：
- 递归中，解决子问题的过程是逐层递归地调用函数，然后逐层返回结果。
- 分治中，解决子问题的过程可以并行地进行，然后将子问题的解合并。