目录
交叉熵的简单理解:真实分布与非真实分布的交叉,完全对应,熵为0
交叉熵的简单理解:真实分布与非真实分布的交叉,完全对应,熵为0

这个式子就是熵的表达式. 简单来说, 其意义就是在最优化策略下, 猜到颜色所需要的问题的个数。熵代表的是随机变量或整个系统的不确定性,熵越大,随机变量或系统的不确定性就越大。
现在已经了解了熵是什么, 那么, 下面解释交叉熵(cross entropy) 的含义.对于第二个例子, 如果仍然使用第一个例子中的策略, 如下图:

1/8 的概率, 硬币是橘色, 需要两个问题, 1/2 的概率是蓝色, 仍然需要两个问题, 也就是说,认为小球的分布为(1/4,1/4,1/4,1/4),这个分布就是非真实分布。平均来说, 需要的问题数是 1/8×2+1/8×2+1/4×2+1/2×2=2。 因此, 在例子二中使用例子一的策略是一个比较差的策略. 其中2是这个方案中的交叉熵。而最优方案的交叉熵是1.75。
给定一个策略, 交叉熵就是在该策略下猜中颜色所需要的问题的期望值。更普遍的说,交叉熵用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出成本的大小。
交叉的字面意思在于:真实分布与非真实分布的交叉。给定一个方案, 越优的策略, 最终的交叉熵越低。具有最低的交叉熵的策略就是最优化策略,也就是上面定义的熵。因此, 在机器学习中, 我们需要最小化交叉熵。完全对应,熵为0
其中, p 是真正的概率, 例如例子二中, 橘色和绿色是 1/8, 红色是 1/4, 蓝色是 1/2。p^是错误地假设了的概率, 例如, 在例子二中我们错误地假设了所有的颜色的概率都是 1/4。p和 p^ 可能有点容易混淆. 记住一点, log是用来计算在 你的策略下猜中所需要的问题数, 因此, log中需要的是你的预测概率p^。在决策树中, 如果建立的树不是最优的, 结果就是对于输出的概率分布的假设是错误地, 导致的直接结果就是交叉熵很高。交叉熵不仅仅应用在决策树中, 在其他的分类问题中也有应用。
分类问题
在二分类问题中, 标签 y 是 1 的似然是对于标签 y 的预测 y^, 同样的, 标签是 0 的似然是 1y^. 我们需要最大化似然函数, 而且, 由于二分类问题的特殊性, 根据伯努力分布(Bernoulli distribution),可以把似然函数写成
当 y=1 的时候, 第二项为 1, 因此, 优化的是 y^
当 y=0 的时候, 第一项为 1, 优化的是 1y^.对上面的似然函数取对数, 结果是:
最大化似然函数, 就是对上面表达式取负然后最小化。也是交叉熵的表达式。 交叉熵有时候也被称为对数损失函数。注意与上边例子区别是多了个负号,上边例子是消除不确定性需要付出的成本;而现在这个加了负号的交叉熵,则是最终的目标函数。
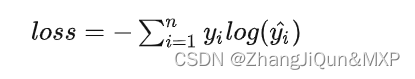
举例来说, 假设我有 3 枚硬币, 正正反, 记为 1,1,0. 预测结果是 0.8, 0.9, 0.3, 那么, 交叉熵的均值是:
1/3(1×log0.8+1×log0.9+(10)×log(10.3))
假设有一个完美的算法, 直接预测出了 1,1,0, 那么交叉熵的结果就是 0.