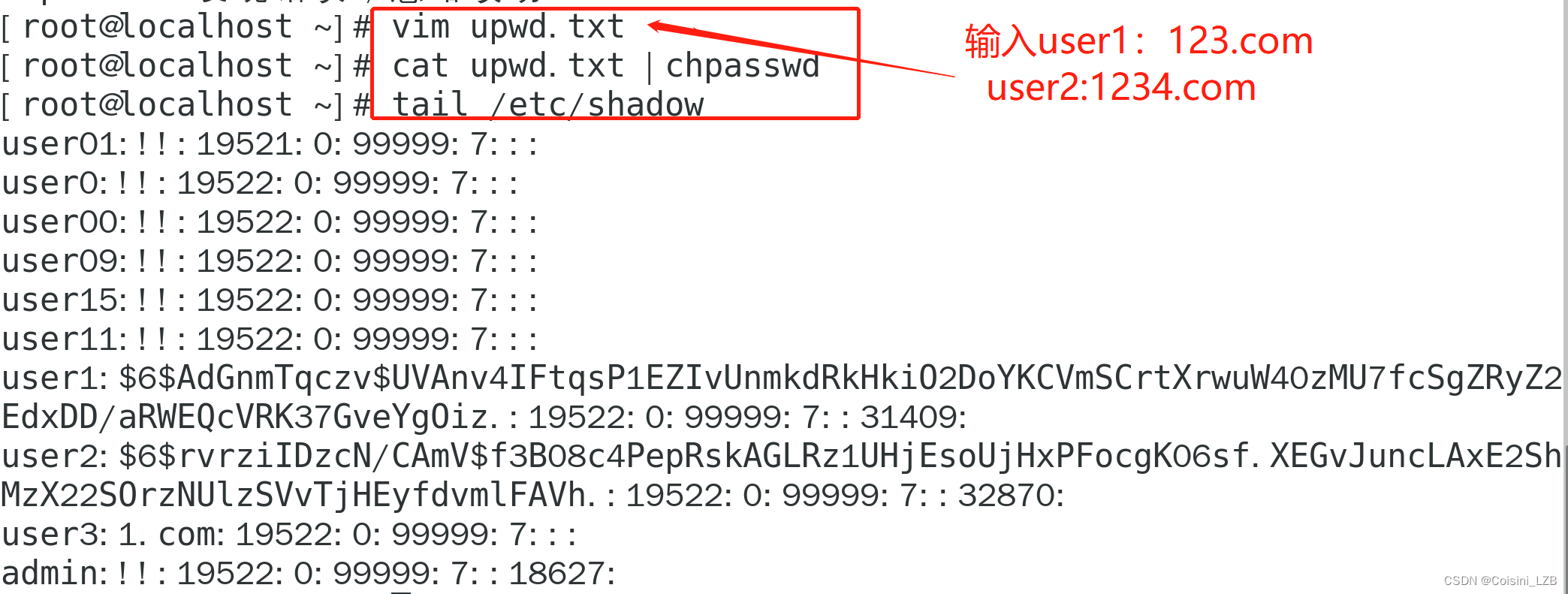
😄嘻嘻，朋友们，大家好！昨天我们学习了左移，今天我们来谈谈右移>>。

⭐️简单来说，右移就是将一个数二进制表达整体向右移动，也就是去掉一个数的二进制表达的末位，右移一位就去掉一位，右移两位就去掉两位。一般情况下右移就是除以2的幂并向下取整。

下面就让我们来详细看看吧！

在这里插入图片描述

文章目录

一、基础知识
- 1️⃣ 右移的二进制表示：
- 2️⃣ 右移的执行结果：
- 3️⃣ 对负数右移：-x>>y=-⌈(x>>y)⌉(不建议用)
- - 1. -9>>1
  - 2. ((unsigned int)-9) >> 2
- 4️⃣ 右移负数位：
二、拓展应用：
- 1. 去除低k位：
- 2. 取第k位的值：
三、写在后面的话：

一、基础知识

✨右移运算符是一个二元运算符，右移操作是也一种位操作，用来将一个数的二进制表达的所有位向右移动指定的位数。

✨我们知道，无符号整数都是非负数，所以负数只出现在有符号整数中。（所以我们这里可以不分有符号整数和无符号整数）：

对于正数，直接右移（左侧添0，可视为不添）
对于负数，右移后左侧添1；0你懂的

1️⃣ 右移的二进制表示：

✨x>>y 表示将x的二进制表达向右移动y位（其中x和y都是整数）。
如：1001 >> 2 ----> 10 （直接去掉后两位）

2️⃣ 右移的执行结果：

✨右移操作相当于将一个数除以2的n次方。
x>>y <=> [ $\frac {x}{2^y}$ ] ,方括号一般认为是向下取整。咦？不是常说右移是除以2，左移是乘以2吗，你这怎么还向下取整了呢？
在这里插入图片描述
👉因为不是所有的数都能被2整除，所以根据C语言右移的规则，应当向下取整。(C语言除法结果是正数则向下取整，结果为负数则向零取整)

所以上面的1001>>2 = [ $\frac {9}{2^2}$ ] = [ $\frac {9}{4}$ ] = 2(向下取整)

代码如下：

#include<stdio.h>int main(void)
{int a = 0b1001;unsigned int b = a ;printf("%d\n", a>>2);printf("%u\n", b>>2);return 0;
}

执行结果如下：

在这里插入图片描述
可以看出结果是9/4=2；
下面我们继续增大右移的位数：

#include<stdio.h>int main(void)
{int a = 0b1001;//9unsigned int b = a ;printf("%d\n", a>>4);printf("%u\n", b>>4);return 0;
}

在这里插入图片描述
可以看出9/16=0，没什么问题。

当然，这里也可以从补码（移位）的角度来解释。9的二进制表达一共4位有效，向右移动4位后显然是0。

3️⃣ 对负数右移：-x>>y=-⌈(x>>y)⌉(不建议用)

注：-x>>y并不等于-(x>>y)

如：-9>>1 是多少呢？相信你心中已经有答案了，请看下图！

#include<stdio.h>int main(void)
{int a = -9;unsigned int b = a ;printf("%d\n", a >> 1);//	-9>>1printf("%d\n", a / 2);//	-9/2printf("%d\n", a>>2);//		-9>>2printf("%d\n", a >> 3);//	-9>>3printf("%u\n", b>>2);//		(unsigned int )-9>>2return 0;
}

执行结果如下：
在这里插入图片描述

我们先来看a，a是一个有符号整数-9，现在对其右移。

1. -9>>1

(1)值的角度：
-9>>1 = [-9/2] = [-4.5] = -5 （向下取整），但-(9>>1)=-([9/2])=-4
注意：这里千万要和-9/2 = -4区分开来！因为在C语言中，对于负数的取整通常是向零取整（向上取整）。也就是说，负数会被取整为最接近且大于等于它的整数。
如：(int)(-3.9) = -3 ；(int)(-2.1) = -2;

对应的符合见下图，左面是向下取整，右面是向上取整：
在这里插入图片描述
下面是它们的图像：

❤️向下取整（高斯函数）：
在这里插入图片描述
❤️向上取整：

这里我就不展开讨论了，以后有机会再深入去了解其二者的相关知识。

(2)补码的角度：
- 9的补码是：00000000 00000000 0000000 00001001
- -9的补码是：11111111 11111111 11111111 11110110 + 1-->11111111 11111111 11111111 11110111
- -9的补码右移一位：11111111 11111111 11111111 11111011(左侧补1)
- 转换成机器数（原码）：10000000 00000000 00000000 00000100+1-->10000000 00000000 00000000 00000101 = -5

😄综上我们得到了-x>>y = -⌈(x>>y)⌉ = -(⌈ $\frac {x}{2^y}$ ⌉)，注意，此处是向上取整，但计算机中默认正整数除法是向下取整，所以你可能要用ceil函数自己处理。

-9>>2,-9>>3与上面的推理过程类似，此处不再赘述！

2. ((unsigned int)-9) >> 2

现在，就让我们来看看上图的最后一个输出，为什么是1073741821呢？

在这里插入图片描述
✨首先，b的类型是unsigned int ，无符号整型，也就是都是非负的。现在我们执行第一个语句：b=a , 将-9赋值给一个无符号整型，b的值将会变成多少呢？这里我们借助昨天的图来进行求解：👇

✨如何求b的值，言下之意就是让我们从0开始往左数9个数，可以轻松得到b的值是2 ^ 32-9,也就是4294967296-9=4294967287。
✨现在，我们得到了((unsigned int)-9) >> 2 <=> 4294967287>>2,下面从两个方面进行求解：

(1)值的角度：然后另b除以4并向下取整，即[4294967287/4]=4294967287/4=1073741821
(2)移位的角度：
1. 因为2 ^ 32-1的二进制表达是：11111111 11111111 11111111 11111111
2. 所以2 ^ 32-9的二进制表达可以写为：11111111 11111111 11111111 11111111-00000000 00000000 00000000 00001000=11111111 11111111 11111111 11110111
3. 现对其右移两位：00111111 11111111 11111111 11111101，然后将其以十进制的形式输出即可。

验证一下输出：

#include<stdio.h>int main(void)
{int b = 0b00111111111111111111111111111101;printf("%d", b);return 0;
}

执行结果如下：
在这里插入图片描述
执行结果正确，证明上述解法可行。

4️⃣ 右移负数位：

✨昨天我们了解了左移负数位的情况，发现那是未定义的行为，现在我们来看看右移负数位又会如何？let's go!!!
在这里插入图片描述
我们先来看一段代码：

#include<stdio.h>int main(void)
{int a = 9;printf("%d\n", a >>  0);printf("%d\n", a >> -1);printf("%d\n", a >> -2);printf("%d\n", a >> -3);return 0;
}

执行结果如下：
在这里插入图片描述

💔咦❓这个输出有点意思，到底是怎么回事呢❓右移负数位竟然没有报错，那就是合理的❓既然合理，那为啥会出现这种结果呢❓按照我们以往的思维，右移-1位就是左移1位啊❗️结果不应该是18吗，怎么不对呢❓阁下莫急，我们接着往下看：

#include<stdio.h>int main(void)
{int a = 9;printf("%d\n", a >>  0);printf("%d\n", a >> -1);printf("%d\n", a >> -2);printf("%d\n", a >> -3);printf("***\n");printf("%d\n", a >> -30);printf("%d\n", a >> -31);printf("%d\n", a >> -32);printf("%d\n", a >> -33);printf("%d\n", a >> -34);printf("%d\n", a >> -35);return 0;
}

执行效果如下：
在这里插入图片描述
💔咦？下面这个结果也有点出乎意料啊！9>>-30结果是2❗️9>>-32结果是9❗️相信如果你对数字比较敏感的话，应该已经发现了右移负数位的规律。当然，如果没有发现也不用着急，我们继续往下看：

#include<stdio.h>int main(void)
{int a = 9;printf("%d\n", a >>  0);printf("%d\n", a >> -1);printf("%d\n", a >> -2);printf("%d\n", a >> -3);printf("***\n");printf("%d\n", a >> -30);printf("%d\n", a >> -31);printf("%d\n", a >> -32);printf("%d\n", a >> -33);printf("%d\n", a >> -34);printf("%d\n", a >> -35);printf("***\n");printf("%d\n", a >> -62);printf("%d\n", a >> -63);printf("%d\n", a >> -64);printf("%d\n", a >> -65);printf("%d\n", a >> -66);printf("%d\n", a >> -67);return 0;
}

在这里插入图片描述
❤️通过第三个代码我们可以看出:
🌟右移-32位的倍数的时候和右移0位时类似，都是其本身;
🌟右移-30位和右移-62位类似，都是2，那2又有什么特殊之处呢？我们来看看它们的补码：

9的原(补)码是：00000000 00000000 00000000 00001001
2的原(补)码是：00000000 00000000 00000000 00000010

可以看出，9>>2 = 2，且32-(abs(-30)%32)=2， 32- (abs(-62)%32)=2

🌟右移-31位和右移-63位类似，都是4

4的原(补)码是：00000000 00000000 00000000 00000100

我们知道9>>1 = 4，且32-(abs(-31)%32)=1， 32- (abs(-63)%32)=1

所以，经过上述的推导我们可以得出右移负数位的计算公式：
若记右移n位（n为负数），并记结果为result，则
result=32-（abs(n)%32)

（此为博主自己总结的结论，如有错误还请指正，如需引用还请注明出处）

当然，右移负数位在平常很少用到（一般都在一定范围内左移或右移，别自己给自己找麻烦）。

二、拓展应用：

✨下面的第k位均为从右往左第k位（从第0位开始数），如果习惯按第1位开始，则可令k=k+1;

1. 去除低k位：

给定一个数x,将其低k位去除后再输出。
方法：直接右移k位即可，x>>k

2. 取第k位的值：

二进制表达只有0或1，所以第k位要么是0，要么是1。
方法：将x右移k位后 和1位于 or 和0位或
(x>>k)&1 or (x>>k)|0

除此之外，还有其他的一些操作，都可以通过位运算的相关定义得出，此处不再赘述！

三、写在后面的话：

🔥自从chatgpt等大语言模型出现之后，立刻就有了相当广泛的应用。不论是商用还是民用，像是平常询问零碎的知识点，聊天，写代码等等，都有了其一席之地。不可否认，它们的确很强大。但随着其进一步发展，就拿CSDN平台来说，无论是问答还是写博客，都或多或少地存在着它们的影子。

🔥先说写博客方面，过分依赖于gpt写的博客和人写的博客其实差异还是蛮大的，因为前者写的大都比较生硬，基本以大片大片的概念为主，缺乏和观者的互动；并且其所述的知识也不一定都是正确的，所以我想说什么，你懂的。

🔥再说问答方面，我无法忍受一个外行人完全借助gpt来回答各行各业的问题，你回答对了我不说什么，但你完全借其所答，拿着错误的答案去回复别人，这既是一种对问者的不尊敬，也是对自己行为的不负责。我认为，它应该成为一种提升自己能力的工具，而不是将其信奉为教条，它可以用来验证我们的想法，也可以帮我们打开思路，但唯独不能代替我们。
在这里插入图片描述