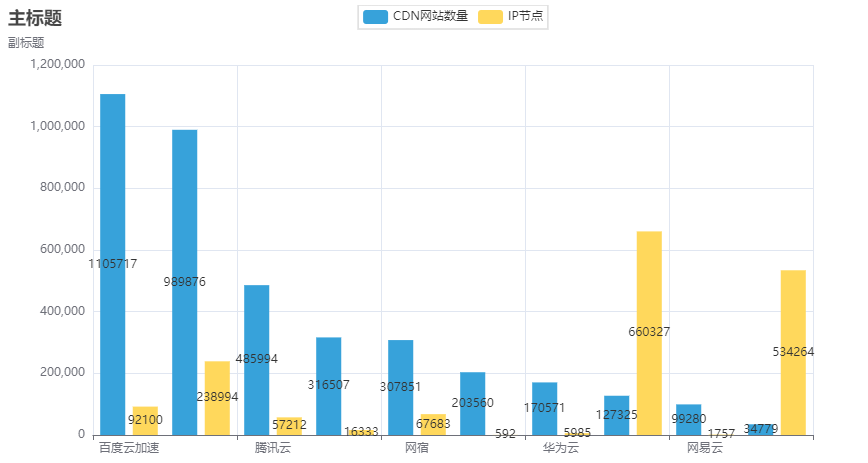
代码示例 :
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><title>Banner 轮播</title><style>/* 取消浏览器或者其它标签的默认的内外边距 */* {margin: 0;padding: 0;}/* 取消列表样式 主要是取消列表的小圆点 */li {list-style: none;}/* 设置图片自适应 */img {width: 100%;}.banner {/* 子绝父相 : 整个父容器需要设置相对定位 内部的子元素使用绝对定位任意摆放 */position: relative;/* 父容器内存尺寸 图片 846x472 需要设置 img 标签图片内容宽度为 100% 自适应 */width: 423px;height: 236px;/* 设置背景 */background-color: pink;/* 上下设置 100 像素边距 左右水平居中 */margin: 100px auto;/* 设置圆角 */border-radius: 20px;/* 超出圆角部分的内容直接隐藏 */overflow: hidden;}/* 并集选择器 将左右按钮中相同的样式提取出来进行设置代码重构 */.left,.right {/* 使用绝对定位 在 相对定位的父容器中任意放置元素 */position: absolute;/* 垂直居中 *//* 首先 走到父容器高度一般 */top: 50%;/* 然后 向上走自己高度的一半 */margin-top: -15px;/*绝对定位的盒子 无须转换,直接给大小就好了*/width: 20px;height: 30px;/* 垂直居中 - 行高 = 高度 */line-height: 30px;/* 半透明黑色背景 */background: rgba(0, 0, 0, .2);/* 取消链接的下划线 */text-decoration: none;/* 设置白色 */color: #fff;}/* 设置向左翻页按钮的样式 绝对定位位置 和 圆角状态样式 */.left {left: 0;/* 复合写法设置圆角矩形 : 左上角 右上角 右下角 左下角 */border-radius: 0 15px 15px 0;}/* 设置向右翻页按钮样式 主要是 绝对定位位置 和 圆角状态样式 */.right {/* 绝对定位右侧 */right: 0;/* 文本右对齐 */text-align: right;/* 复合写法设置圆角矩形 : 左上角 右上角 右下角 左下角 */border-radius: 15px 0 0 15px;}/* 按钮移动后的样式 背景颜色加深一倍 */.left:hover,.right:hover {background: rgba(0, 0, 0, .4);}/* 底部小圆点容器 */.circles {/* 在 相对定位 父容器中 使用 绝对定位 任意摆放 */position: absolute;/* 设置底部小圆点容器居中 *//* 首先 走到父容器宽度的一半 */left: 50%;/* 然后 向左走自己的一半宽度 */margin-left: -35px;/* 绝对定位 下边偏移 15 像素 距离底部 15 像素 */bottom: 15px;/* 设置小圆点父容器的尺寸 */width: 70px;height: 13px;/* 设置小圆点背景 半透明白色 */background: rgba(255, 255, 255, 0.3);/* 四个角都设置 7 像素的圆角 */border-radius: 7px;}/* 设置单个小圆点样式 */.circles li {/* 设置浮动样式 */float: left;/* 小圆点宽高都是 8 像素 设置 50% 或者 4 像素 圆角就可以变为正园 */width: 8px;height: 8px;/* 小圆点默认白色 */background-color: #fff;/* 小圆点分开 */margin: 3px;/* 设置四个方向的圆角为 50% 使得正方形变为圆形 */border-radius: 50%;}/* 被选中的小圆点样式此处注意选择器的优先级 */.circles .current {/* 被选中的 */background-color: #ff5000;}</style>
</head>
<body><div class="banner"><!-- 向左翻页按钮 --><a href="#" class="left"> < </a><!-- 向右翻页按钮 --><a href="#" class="right"> > </a><!-- Banner 图片 --><img src="banner_image.png" alt=""><!-- 底部的小圆点 --><ul class="circles"><li></li><!-- 当前选择的小圆点 --><li class="current"></li><li></li><li></li><li></li></ul></div>
</body>
</html>