目录
1.概述
2.线性结构
3.时间复杂度
4.查找算法
5.树
6.图
1.概述
博主之前写过一个完整的关于数据结构的系列文章,一共十三篇,内容包含,数组、链表、堆栈、队列、时间复杂度、顺序查找、二分查找、二叉树、二叉搜索树、平衡二叉树、红黑树、B树、B+树、大顶堆、小顶堆、图、DFS、BFS、最短路径算法。由于各篇文章分的比较散,本文中将对做一次清单式的总结,这是一份属于你的数据结构大全,请签收。
2.线性结构
文章链接:
数据结构(1)线性结构——数组、链表、堆栈、队列(介绍和JAVA代码实现)_线性结构中队列、数组、栈结构__BugMan的博客-CSDN博客
在线性数据结构中,数据元素之间存在一对一的关系,每个数据元素最多有一个直接前驱和一个直接后继。这种结构中,数据元素按照一定的顺序排列,形成一个线性序列。常见的线性数据结构包括数组、链表、栈和队列。
以下是一些常见的线性数据结构及其特点:
- 数组(Array)
- 数组是一种固定大小的线性结构,它在内存中分配一块连续的存储空间,用于存储相同类型的数据元素。
- 数组的访问是基于索引的,索引从 0 开始,通过索引可以快速访问数组中的元素。
- 插入和删除操作可能需要移动其他元素,因此在数组中执行这些操作可能较慢。
- 链表(Linked List)
- 链表是一种由节点组成的线性结构,每个节点包含数据元素和一个指向下一个节点的引用(或指针)。
- 链表分为单向链表和双向链表。双向链表的节点还包含一个指向前一个节点的引用。
- 链表的插入和删除操作相对较快,因为不需要移动其他元素,但访问元素可能较慢,需要遍历链表。
- 栈(Stack)
- 栈是一种后进先出(LIFO,Last In First Out)的线性结构,只能在栈顶进行插入和删除操作。
- 栈可以用于实现函数调用、表达式求值等场景,常用的操作包括压栈(push)和弹栈(pop)。
- 队列(Queue)
- 队列是一种先进先出(FIFO,First In First Out)的线性结构,元素只能从队列的一端插入,从另一端删除。
- 队列常用于实现任务调度、广度优先搜索等场景,常用的操作包括入队(enqueue)和出队(dequeue)。
3.时间复杂度
文章链接:
数据结构(2)时间复杂度——渐进时间复杂度、渐进上界、渐进下界__BugMan的博客-CSDN博客
时间复杂度是算法分析中用来衡量算法执行时间随输入规模增长而增长的速率。它通常用大O符号(O)来表示。时间复杂度不考虑精确的执行时间,而是关注算法运行时间的增长趋势。
时间复杂度分析的目的是衡量算法在不同规模的输入下的性能表现,从而可以选择更高效的算法来解决问题。
以下是一些常见的时间复杂度:
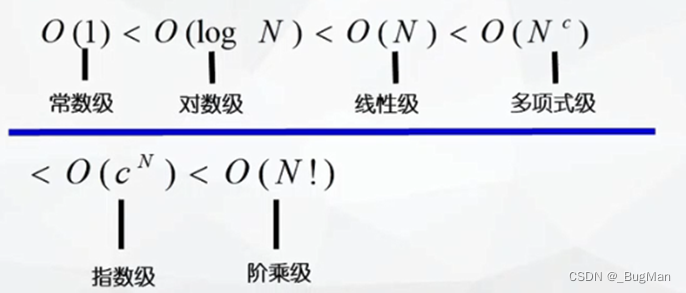
- O(1) - 常数时间复杂度
- 表示算法的执行时间与输入规模无关,无论输入多大,执行时间恒定。
- 典型的例子是访问数组中的特定元素、执行固定次数的操作等。
- O(log n) - 对数时间复杂度
- 表示算法的执行时间与输入规模的对数呈线性关系,随着输入规模增大,执行时间增长较慢。
- 典型的例子是二分查找,每次迭代将搜索范围缩小一半。
- O(n) - 线性时间复杂度
- 表示算法的执行时间与输入规模成线性关系,随着输入规模增大,执行时间也会线性增长。
- 典型的例子是对数组进行遍历、查找最大/最小值等。
- O(n log n) - 线性对数时间复杂度
- 表示算法的执行时间介于线性和平方之间,通常在大多数情况下,效率很高。
- 典型的例子是快速排序和归并排序。
- O(n^2) - 平方时间复杂度
- 表示算法的执行时间与输入规模的平方成正比,随着输入规模增大,执行时间迅速增长。
- 典型的例子是嵌套循环,例如选择排序和插入排序。
- O(n^k) - 多项式时间复杂度
- 表示算法的执行时间与输入规模的某个常数幂成正比,k 是一个常数。
- 典型的例子是冒泡排序等。
- O(2^n) - 指数时间复杂度
- 表示算法的执行时间随着输入规模呈指数级增长,通常效率非常低。
- 典型的例子是递归穷举算法。
4.查找算法
文章链接:
数据结构(3)基础查找算法——顺序查找、二分查找(JAVA版)__BugMan的博客-CSDN博客
查找算法,本系列包括两种:
- 线性查找(Sequential Search)
- 线性查找是最简单的查找算法,逐个遍历数据集合,比较每个元素是否与目标元素相等。
- 时间复杂度:O(n)(最坏情况下需要遍历所有元素)。
- 二分查找(Binary Search)
- 二分查找要求数据集合已排序。它将数据集合一分为二,然后与中间元素比较,根据比较结果确定目标元素在哪一半中,然后递归进行查找。
- 时间复杂度:O(log n)(每次比较都将数据集合减半)。
- 仅适用于有序数据。
5.树
树形结构里,本系列包含:
- 二叉树
- 二叉搜索树
- 平衡二叉树
- 红黑树
- B树
- B+树
文章链接:
数据结构(4)树形结构——二叉树(概述、前序、中序、后序、层序遍历JAVA实现)_树形图的结点顺序__BugMan的博客-CSDN博客
数据结构(5)树形结构——二叉搜索树(JAVA代码实现)_树形结构搜索__BugMan的博客-CSDN博客
数据结构(6)树形结构——平衡二叉树(JAVA代码实现)_java 平衡二叉树__BugMan的博客-CSDN博客
数据结构(7)树形结构——红黑树(概念、插入过程、删除过程)_红黑树1的插入和删除__BugMan的博客-CSDN博客
数据结构(8)树形结构——B树、B+树(含完整建树过程)_b+树结构__BugMan的博客-CSDN博客
数据结构(9)树形结构——大顶堆、小顶堆__BugMan的博客-CSDN博客
-
二叉树: 二叉树是一种树状结构,每个节点最多有两个子节点,称为左子节点和右子节点。它的节点可以为空,或者包含一个值和指向左右子节点的指针。二叉树在很多领域中有广泛的应用,如表达式求值、搜索和排序。
-
二叉搜索树: 二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,对于每个节点,其左子树的所有节点值都小于该节点值,右子树的所有节点值都大于该节点值。这种有序性质使得二叉搜索树在查找、插入和删除操作上具有高效性能。
-
平衡二叉树: 平衡二叉树是一种特殊的二叉搜索树,其左右子树的高度差(平衡因子)不超过某个固定值。这保证了树的高度保持在较小的范围内,从而保证了查找、插入和删除操作的平均时间复杂度为 O(log n)。
-
红黑树: 红黑树是一种自平衡的二叉搜索树,它通过在插入和删除操作中进行颜色变换和旋转来保持树的平衡。红黑树的特点包括:每个节点是红色或黑色,根节点是黑色,每个叶子节点(NIL 节点)都是黑色,红色节点的子节点必定为黑色,从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点。
-
B树: B树(B-tree)是一种多叉树,用于存储大量的有序数据。B树的特点包括:每个节点可以包含多个子节点,一个节点可以包含多个关键字,子节点的关键字范围和父节点的关键字范围有重叠,保证了树的平衡性和高效的查找性能。
-
B+树: B+树(B+ tree)是一种在B树基础上进行了优化的数据结构,主要用于磁盘存储和数据库索引。与B树不同,B+树的所有关键字都出现在叶子节点中,非叶子节点只包含指向叶子节点的指针。这种结构可以提高磁盘存储的效率,同时适合范围查询。
6.图
图,在本系列种包含:
- 图的存储和表示
- 图的深度遍历和广度遍历
- 图的最短路径算法
- 最小生成树
文章链接:
数据结构(10)图的概念、存储_数据结构中图的存储概念__BugMan的博客-CSDN博客
数据结构(11)图的遍历,DFS、BFS的JAVA实现_java实现bfs和dfs__BugMan的博客-CSDN博客
数据结构(12)Dijkstra算法JAVA版:图的最短路径问题_dijkstra算法求解最短路径例题java__BugMan的博客-CSDN博客
数据结构(3)基础查找算法——顺序查找、二分查找(JAVA版)__BugMan的博客-CSDN博客