近似训练
近似训练(Approximate Training)是指在机器学习中使用近似的方法来训练模型,以降低计算复杂度或提高训练效率。这种方法通常用于处理大规模数据集或复杂模型,其中精确的训练算法可能过于耗时或计算资源不足。
近似训练的主要思想是通过在训练过程中引入一些近似技巧或近似算法,以在准确性和效率之间取得平衡。以下是一些常见的近似训练方法:
-
随机采样:在训练过程中,通过从数据集中随机采样一部分样本来训练模型,而不是使用完整的数据集。这种方法可以提高训练速度,但可能会引入一定的估计误差。
-
小批量训练:将数据集划分为小批量(mini-batch),每次使用一个小批量的样本进行梯度计算和参数更新。相比于全批量训练,小批量训练可以减少计算开销,并在一定程度上保持模型的准确性。
-
参数量化:将模型的参数进行量化或压缩,以减少模型的存储空间和计算复杂度。这可以通过使用低精度表示(如浮点数的低位表示)或使用特殊的压缩算法来实现。
-
近似损失函数:使用近似的损失函数来代替原始的损失函数。这种方法可以简化计算或优化过程,并在某些情况下仍能保持模型的性能。
-
近似优化算法:使用近似的优化算法来更新模型参数。这些算法通常通过减少每次迭代的计算量或降低计算复杂度来提高训练效率。
本章我们讲解的近似方法,主要是为了解决跳元模型和连续词袋模型中softmax大量求和计算提出。
文章内容来自李沐大神的《动手学深度学习》并加以我的理解,感兴趣可以去https://zh-v2.d2l.ai/查看完整书籍
文章目录
- 近似训练
- 负采样
- 层序Softmax
负采样
负采样修改了原目标函数。给定中心词 w c w_c wc的上下文窗口,任意上下文词 w o w_o wo来自该上下文窗口的被认为是由下式建模概率的事件:
P ( D = 1 ∣ w c , w o ) = σ ( u o T v c ) P(D=1|w_c,w_o)=\sigma(u_o^Tv_c) P(D=1∣wc,wo)=σ(uoTvc)
对于词典中索引为 i i i的任何词,分别用 v i ∈ R d v_i\in R^d vi∈Rd和 u i ∈ R d u_i\in R^d ui∈Rd表示其用作中心词和上下文词时的两个向量。
其中 σ \sigma σ使用了sigmoid激活函数的定义:
σ ( x ) = 1 1 + e x p ( − x ) \sigma(x)=\frac{1}{1+exp(-x)} σ(x)=1+exp(−x)1
让我们从最大化文本序列中所有这些事件的联合概率开始训练词嵌入。具体而言,给定长度为 T T T的文本序列,以 w ( t ) w^{(t)} w(t)表示时间步 t t t的词,并使上下文窗口为 m m m,考虑最大化联合概率:
∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( D = 1 ∣ w ( t ) , w ( t + j ) ) \prod_{t=1}^{T}\prod_{-m\leq j \leq m,j\neq 0}P(D=1|w^{(t)},w^{(t+j)}) t=1∏T−m≤j≤m,j=0∏P(D=1∣w(t),w(t+j))
然而, 上述式子只考虑那些正样本的事件。仅当所有词向量都等于无穷大时, 式子中的联合概率才最大化为1。当然,这样的结果毫无意义。为了使目标函数更有意义,负采样添加从预定义分布中采样的负样本。
用 S S S表示上下文词 w o w_o wo来自中心词 w c w_c wc的上下文窗口的事件。对于这个涉及 w o w_o wo的事件,从预定义分布 P ( w ) P(w) P(w)中采样 K K K个不是来自这个上下文窗口噪声词。用 N k N_k Nk表示噪声词 w k w_k wk( k = 1 , . . . , K k=1,...,K k=1,...,K)不是来自 w c w_c wc的上下文窗口的事件。假设正例和负例 S , N 1 , N 2 , . . . , N k S,N_1,N_2,...,N_k S,N1,N2,...,Nk的这些事件是相互独立的。负采样将上式中的联合概率(仅涉及正例)重写为
∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( w ( t + j ) ∣ w ( t ) ) \prod_{t=1}^{T}\prod_{-m\leq j \leq m,j\neq 0}P(w^{(t+j)}|w^{(t)}) t=1∏T−m≤j≤m,j=0∏P(w(t+j)∣w(t))
通过事件 S , N 1 , . . . , N k S,N_1,...,N_k S,N1,...,Nk近似条件概率:
P ( w ( t + j ) ∣ w ( t ) ) = P ( D = 1 ∣ w c , w o ) ∏ k = 1 , w k P ( w ) K P ( D = 0 ∣ w ( t ) , w k ) P(w^{(t+j)}|w^{(t)})=P(D=1|w_c,w_o)\prod_{k=1,w_k~P(w)}^{K}P(D=0|w^{(t)},w_k) P(w(t+j)∣w(t))=P(D=1∣wc,wo)k=1,wk P(w)∏KP(D=0∣w(t),wk)
在这个公式中, P ( w ( t + j ) ∣ w ( t ) ) P(w^{(t+j)}|w^{(t)}) P(w(t+j)∣w(t)) 表示在给定中心词 w ( t ) w^{(t)} w(t) 的情况下,目标词 w ( t + j ) w^{(t+j)} w(t+j) 出现的概率。这个概率可以通过两个因素来计算:正例概率 P ( D = 1 ∣ w c , w o ) P(D=1|w_c,w_o) P(D=1∣wc,wo) 和负例概率的乘积。
正例概率 P ( D = 1 ∣ w c , w o ) P(D=1|w_c,w_o) P(D=1∣wc,wo) 表示在给定中心词 w c w_c wc 和上下文词 w o w_o wo 的情况下,目标词 w o w_o wo 是中心词 w c w_c wc 的上下文词的概率,即它们在给定上下文中存在关联的概率。
负例概率的乘积部分表示在给定中心词 w ( t ) w^{(t)} w(t) 的情况下,其他词 w k w_k wk (其中 k k k 的范围是从 1 到 K K K,表示负例的数量)不是中心词的上下文词的概率。这里使用了一个分布 P ( w ) P(w) P(w) 来表示词 w k w_k wk 的概率分布,通常可以根据词的频率来定义分布。
因此,公式中的乘积部分 ∏ k = 1 , w k ∼ P ( w ) K P ( D = 0 ∣ w ( t ) , w k ) \prod_{k=1,w_k\sim P(w)}^{K} P(D=0|w^{(t)},w_k) ∏k=1,wk∼P(w)KP(D=0∣w(t),wk) 表示对于每一个负例词 w k w_k wk,在给定中心词 w ( t ) w^{(t)} w(t) 的情况下,词 w k w_k wk 不是中心词的上下文词的概率。
分别用 i t i_t it和 h k h_k hk表示词 w ( t ) w^{(t)} w(t)和噪声词 w k w_k wk在文本序列的时间步 t t t处的索引。上述式子中关于条件概率的对数损失为:
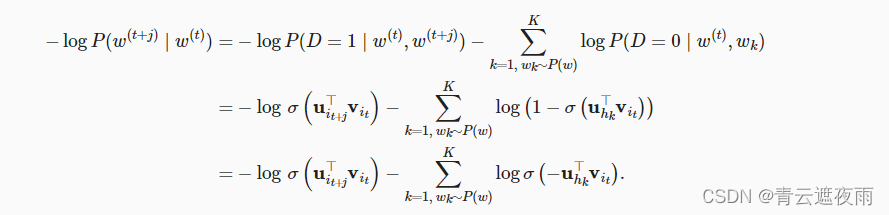
我们可以看到,现在每个训练步的梯度计算成本与词表大小无关,而是线性依赖于 K K K。当将超参数 K K K设置为较小的值时,在负采样的每个训练步处的梯度的计算成本较小。
层序Softmax
作为另一种近似训练方法,层序Softmax(hierarchical softmax)使用二叉树,其中树的每个叶节点表示词表 V V V中的一个词。
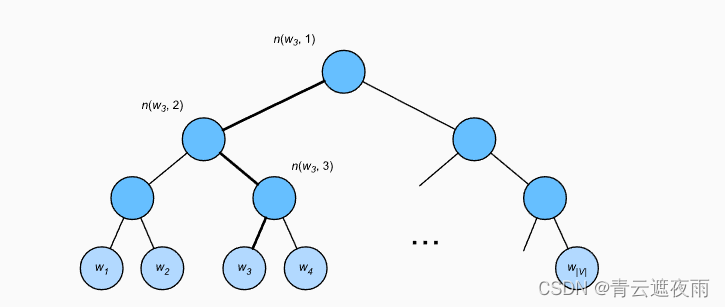 用于近似训练的分层softmax,其中树的每个叶节点表示词表中的一个词
用于近似训练的分层softmax,其中树的每个叶节点表示词表中的一个词
用 L ( w ) L(w) L(w)表示二叉树中表示字 w w w的从根节点到叶节点的路径上的节点数(包括两端)。设 n ( w , j ) n(w,j) n(w,j)为该路径上的 j t h j^{th} jth节点,其上下文字向量为 u n ( w , j ) u_{n(w,j)} un(w,j)。例如, 上图中的 L ( w 3 ) = 4 L(w_3)=4 L(w3)=4。分层softmax将上一节条件概率近似为:
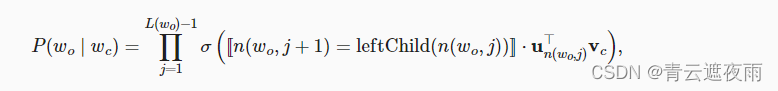
为了说明,让我们计算图中给定词 w c w_c wc生成词 w 3 w_3 w3的条件概率。这需要 w 3 w_3 w3的词向量 v c v_c vc和从根到 w 3 w_3 w3的路径( 图中加粗的路径)上的非叶节点向量之间的点积,该路径依次向左、向右和向左遍历:
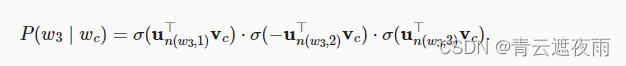
由 σ ( x ) + σ ( − x ) = 1 \sigma(x)+\sigma(-x)=1 σ(x)+σ(−x)=1,它认为基于任意词 w c w_c wc生成词表 V V V中所有词的条件概率总和为1:
∑ w ∈ V P ( w ∣ w c ) = 1 \sum_{w\in V}P(w|w_c)=1 w∈V∑P(w∣wc)=1
幸运的是,由于二叉树结构, L ( w o ) − 1 L(w_o)-1 L(wo)−1大约与 O ( l o g 2 ∣ V ∣ ) O(log_2|V|) O(log2∣V∣)是一个数量级。当词表大小 V V V很大时,与没有近似训练的相比,使用分层softmax的每个训练步的计算代价显著降低。