第一章知识点回顾
表1变量符号对照表

1.1数学期望
数学期望表示为每次可能的结果乘上结果概率的总和。
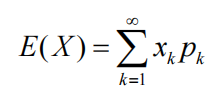
1.1.1 数学期望的性质
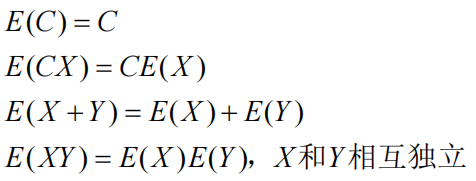
1.2 方差(variance)
概率论中和统计中的方差反映单个(一维)随机变量的离散程度即随机变量偏离数学期望的幅度大小,方差越大偏离数学期望的幅度越大。
总体方差:

离散型随机变量的方差:

1.2.1 方差的性质

1.3 协方差(Covariance)
协方差反映两个(二维)随机变量的相似程度,当两个变量相同时,协方差为方差。“协”是指几个变量的协同相关性。
随机变量X和Y的协方差表示为

如果一个变量大于该变量的期望,另一个变量也大于自身的期望,则两个变量的协方差为正值,正相关。
如果一个变量小于该变量的期望,另一个变量也小于自身的期望,则两个变量的协方差为负值,负相关。
如果一个变量等于该变量的期望,另一个变量也等于自身的期望,则两个变量的协方差为零,不相关,即两个 随机变量相互独立。
1.3.1协方差的性质
假设常数为A和B,随机变量X和Y,且X和Y不是相互独立的,则

1.4协方差矩阵
协方差只能两个(二维)随机变量,三个(三维)及以上随机变量需要计算多个协方差,用矩阵形式表示就是协方差矩阵。协方差矩阵是一个对称非负定矩阵。
二维随机变量X和Y的协方差矩阵表示为

三维随机变量X、Y和Z的协方差矩阵表示为

1.4.1协方差矩阵的性质
假设矩阵为A,向量为b,随机变量X、Y和Z,则
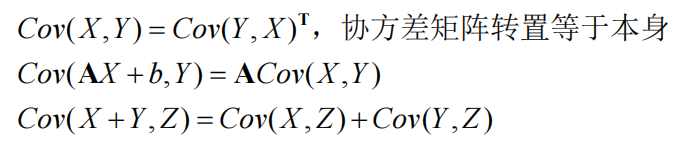
1.5高斯分布
高斯分布也称为正态分布或常态分布,很多信号噪声和数据都服从高斯分布。高斯分布在线性变换后仍然是高斯分布。高斯分布的期望、平均数、中位数和众数相同。
随机变量X服从高斯分布,记为

当期望为0,标准差为1时,高斯分布为标准高斯分布。
高斯分布只要确定了期望和方差就可以得到概率密度函数,表示为

期望决定高斯分布位置,标准差决定高斯分布的幅度。离期望越近概率越大,离期望越远概率越小。标准差越大分布越分散,标准差越小分布越集中。
1.5.1高斯分布的性质
假设实数为A和B,独立高斯随机变量X和Y,则

1.6微分法矩阵求导
1.6.1矩阵转置的性质

1.6.2矩阵微分运算法则

1.6.3矩阵迹的性质

1.6.4矩阵求导求解步骤
- 根据给定的f寻找df。
- 给df套上迹Tr,并进行化简处理。
- 根据导数与微分的关系得到结果。

1.6.5迹函数对矩阵求导
下面两个例子迹函数对矩阵A求导,根据求解步骤计算。
根据矩阵微分运算法则得到

根据导数和微分的关系

第二章卡尔曼滤波
2.1卡尔曼滤波定义
卡尔曼滤波是一种状态观测器、是一种最优化估计算法、是一种传感器数据融合算法。
针对线性系统采用卡尔曼滤波,针对非线性系统采用扩展卡尔曼滤波。区别在于扩展卡尔曼滤波多了一个把预测和测量部分进行线性化的过程。
卡尔曼滤波假设所有变量和噪声都服从高斯分布。卡尔曼滤波由两种变量构成,一种是由数学模型或经验得出的估计(预测)状态变量,另一种是由传感器测量得到的测量(观测)变量,这两种变量都是带误差的变量,卡尔曼滤波将估计状态变量和测量变量进行数据融合,根据上一时刻的变量值循环往复,不停迭代逼近真实的数据,即根据上一时刻的最优估计值预测当前时刻的最优估计值,并使用当前时刻的传感器测量值修正估计值得到最优估计值。
卡尔曼滤波的优点是将不准确的估计值和不准确的测量值做数据融合得到最优估计值,不需要很久之前的数据,只需要上一时刻的数据,运行速度快,占用系统内存小。
2.2卡尔曼滤波公式推导
表2变量符号对照表

注:表2中的先验估计值是不完整的估计,需要用测量值修正处理;后验估计值是卡尔曼滤波输出的最优估计值;观测值是用传感器测量的测量值。
2.2.1递归思想
在时刻1,2,…,k分别测量到数据z1,z2,…,zk,在k时刻的估计值为

当测量数据的足够多时,k趋于无穷,测量值zk不再重要,估计值趋于上一次的估计值。但是当测量数据较少时,k趋于0,测量值zk很重要。

令
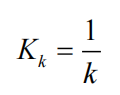
得到卡尔曼增益

当前估计值和上一时刻估计值有关,上一时刻估计值又和上上一次估计值有关,这就是卡尔曼滤波的递归思想,只需要上一时刻的数据就可以估计出当前时刻的值。
估计误差

测量误差
![]()
卡尔曼增益

当k-1时刻的估计误差远大于k时刻的测量误差时,卡尔曼增益趋于1,k时刻估计值趋于k时刻的测量值。

当k-1时刻的估计误差远小于k时刻的测量误差时,卡尔曼增益趋于0,k时刻估计值趋于k-1时刻的估计值。

2.2.2卡尔曼公式

2.2.3卡尔曼增益推导
系统的状态方程

系统的观测方程

过程噪声和测量噪声都是不可以直接测量的,假设过程噪声和测量噪声都服从高斯分布,过程噪声的概率密度函数是期望为0,协方差矩阵为Q;测量噪声的概率密度函数是期望为0,协方差矩阵为R。
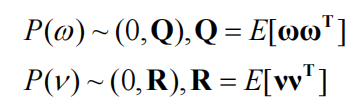
过程噪声协方差矩阵Q的期望计算如下,同理测量噪声协方差矩阵R。

根据方差和协方差定义,且期望为0。

得到

在求解时,系统的状态方程去掉过程噪声,得到一个算出来的卡尔曼预测公式—先验估计值(不完整的估计,需要用测量值修正处理)。

系统的观测方程去掉测量噪声,根据实际测量值zk,得到一个测出来的估计值

卡尔曼滤波器根据上面的不准确的计算出来的先验估计值和不准确的测出来的估计值计算出后验估计值(注意:后验估计值就是最优估计值)。下面公式根据递归和数据融合思想得到。

令

得到卡尔曼校正公式—后验估计

目标是计算卡尔曼增益Kk使后验估计值趋于真实值。Kk与过程噪声和测量噪声有关。引入真实值和后验估计值误差ek,ek的概率密度函数是期望为0,协方差为P的高斯分布。
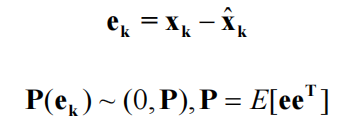
当后验估计值估计越准确即越接近于真实值,ek的方差越小,协方差矩阵Pk的迹Tr(Pk)越小。目标是计算Kk使Tr(Pk)最小。
ek的协方差矩阵Pk

将后验估计和系统的观测方程代入协方差矩阵,这里使用真实测量值zk引入测量噪声进行估计。


令

得到

计算协方差矩阵的第2项

同理,协方差矩阵的第3项也为0。

目标是使协方差矩阵Pk的迹tr(Pk)最小,从而使误差ek的方差最小。
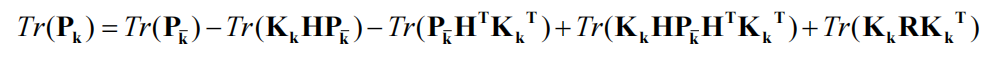
上式等号右边第二项

由互为转置的矩阵迹相同,得到

计算迹在Kk的变化下最小值

根据矩阵微分运算法则和矩阵迹的性质,迹函数对矩阵求导得到卡尔曼校正公式—卡尔曼增益

当测量噪声R很大时

当测量噪声R很小时

2.2.4更新误差协方差矩阵推导
误差协方差矩阵带入卡尔曼增益得到卡尔曼校正公式—更新误差协方差矩阵

2.2.5先验误差协方差矩阵推导
先验误差

带入真实值和先验估计值


先验误差协方差矩阵定义为

判断上式中独立的项

化简得到卡尔曼预测公式—先验误差协方差矩阵

2.3卡尔曼滤波仿真
仿真文件上传到博客中,可以下载进行调试学习。


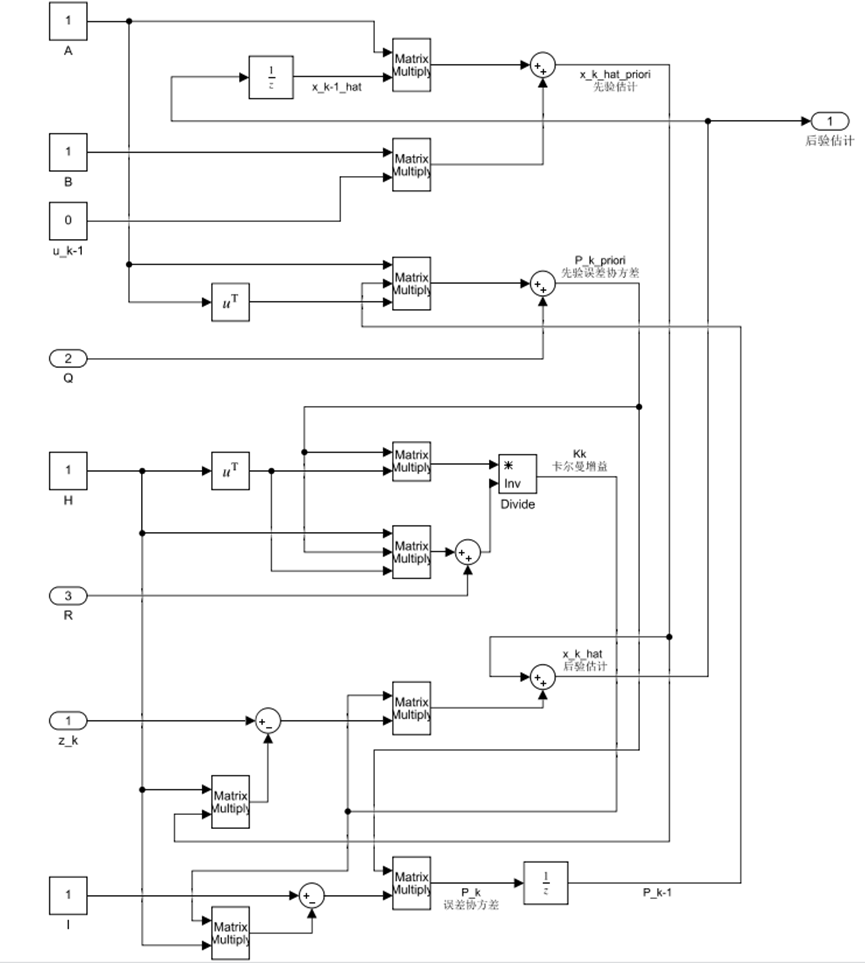
2.4卡尔曼滤波参数调整
2.4.1参数调整方法
通过Simulink仿真可以得到卡尔曼滤波参数调整的方法,可以用于嵌入式系统控制算法中。
Q和R不能为0。当Q等于0时,后验估计等于初值。当R等于0时,系统更相信测量值,后验估计等于测量值。
卡尔曼增益是由Q和R共同作用的,不能单独调整某一个值。同时增大Q和R相同倍数,后验估计变化不大。
减小Q,增大R,卡尔曼增益变小,后验估计收敛速度变慢,振荡小、滞后大、更稳定、更相信估计值;增大Q,减小R,卡尔曼增益变大,后验估计收敛速度快、振荡大、不稳定、更相信测量值。
2.4.2选择Q和R的数值
Q数值的选择,使用数学模型的误差或由实验测得。R数值的选择,使用传感器给定的误差或者由实验测得。
因为卡尔曼增益是由Q和R共同作用的,所以将Q数值设置为固定值,根据实际应用中传感器的变化调整R数值。
2.4.3初值设置
H初值可以设置为1。
xk初值可以设置为0。
Pk初值一般设置为1,不能设为0。多次迭代后,Pk值就趋向稳定值。
参考文献
学习B站DR_CAN的系列视频、百度百科、CSDN和知乎一些大神的博客。