🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
文章目录
- 数据预处理
- 数据变换
- 数据清洗
- 缺失值处理
- 异常值处理
数据预处理
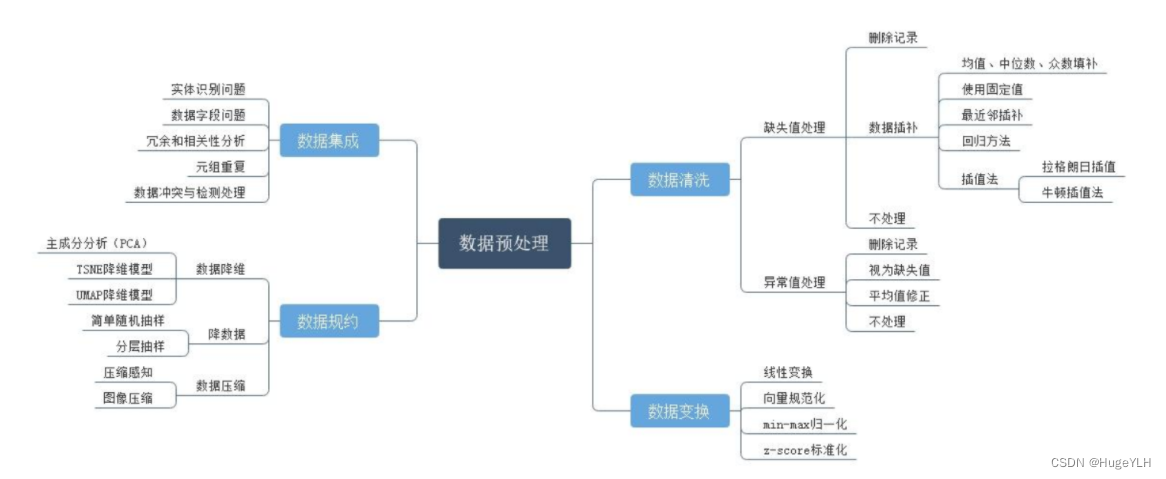
数据变换
常见的数据变换的方式:通过某些简单的函数进行数据变换。
x ′ = x 2 x ′ = x x ′ = log ( x ) ∇ f ( x k ) = f ( x k + 1 ) − f ( x k ) \begin{aligned}&x^{\prime}=x^2 \\&\begin{aligned}x^{\prime}=\sqrt{x}\end{aligned} \\&x'=\log(x) \\\nabla f\left(x_{k})\right.&=f(x_{k+1})-f(x_k) \end{aligned} ∇f(xk)x′=x2x′=xx′=log(x)=f(xk+1)−f(xk)
- 数据指标的一致化处理:
- 极小型
- 极大型
- 中间型
- 区间型
- 数据指标的无量纲化处理:
-
零 - 均值规范化:也叫做标准差规范化,经过处理后的数据平均值为 0,标准差为1。 x ‾ \overline x x 为原数据的均值, σ \sigma σ 为标准差。
x ∗ = x − x ‾ σ x^*=\frac{x-\overline{x}}\sigma x∗=σx−x
-
极值差法:又叫最小 - 最大规范化,离差标准化,将数据映射到 [ 0 , 1 ] [0,1] [0,1] 之间。
x ∗ = x − m i n m a x − m i n x^*=\frac{x-min}{max-min} x∗=max−minx−min
-
功效系数法:就是上一步极值差法然后加了一个偏移量: c c c ,使得最后结果落于 [ c , c + n ] [c,c+n] [c,c+n] 中
-
数据变换的应用方式:数据的标准化,目的是为了消除指标之间的量纲和大小不一的影响,需要进行数据标准化处理。
因此可以将数据按照比例进行缩放,使之落入一个据标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,从而进行综合分析。如将工资收入属性值映射到[-1,1]或者[0,1]之间。
function data1=mfunc_calculate(data,zhibiao_label)% 指标的正向化处理 1 2 极大型;3 4 5 极小型;6 单点最优;7 区间最优if isa(data,'double')for i=1:length(zhibiao_label)if (zhibiao_label(i)==1)data1(:,i)=zheng1(data(:,i));elseif (zhibiao_label(i)==2)data1(:,i)=zheng2(data(:,i));elseif (zhibiao_label(i)==3)data1(:,i)=fu3(data(:,i));elseif (zhibiao_label(i)==4)data1(:,i)=fu4(data(:,i));elseif (zhibiao_label(i)==5)data1(:,i)=fu5(data(:,i));elseif (zhibiao_label(i)==6)prompt = '这是单点最优,请输入单点最优值 ';a = input(prompt);data1(:,i)=qu6(data(:,i),a);elseif (zhibiao_label(i)==7)prompt = '这是区间最优,请输入单点最区间如[5,10] ';aa=input(prompt);data1(:,i)=qu7(data(:,i),aa(1),aa(2));endendelseif isa(data,'cell')% data2=data;for j=1:length(data)data2=data{j};if size(zhibiao_label,1)==1zhibiao_label1=repmat(zhibiao_label,3,1);elsezhibiao_label1=zhibiao_label;endfor i=1:length(zhibiao_label1(j,:))if (zhibiao_label(i)==1)data1{j}(:,i)=zheng1(data2(:,i));elseif (zhibiao_label(i)==2)data1{j}(:,i)=zheng2(data2(:,i));elseif (zhibiao_label(i)==3)data1{j}(:,i)=fu3(data2(:,i));elseif (zhibiao_label(i)==4)data1{j}(:,i)=fu4(data2(:,i));elseif (zhibiao_label(i)==5)data1{j}(:,i)=fu5(data2(:,i));elseif (zhibiao_label(i)==6)prompt = '这是单点最优,请输入单点最优值 ';a = input(prompt);data1{j}(:,i)=qu6(data2(:,i),a);elseif (zhibiao_label(i)==7)prompt = '这是区间最优,请输入单点最区间如[5,10] ';aa=input(prompt);data1{j}(:,i)=qu7(data2(:,i),aa(1),aa(2));endendendendendfunction data=zheng1(data1)%正向指标1% 填1的时候选择data=(data1-min(data1))./(max(data1)-min(data1));endfunction data=zheng2(data1)%正向指标2% 填2的时候选择data=data1;endfunction data=fu3(data1)%负向指标1% 填3的时候选择data=(max(data1)-data1)./(max(data1)-min(data1));endfunction data=fu4(data1)%负向指标2% 填4的时候选择data=(max(data1)-data1);endfunction data=fu5(data1)%负向指标3% 填5的时候选择data=1./(max(abs(data1))+data1);endfunction data=qu6(data1,a)%某点最优% 填6的时候选择data=1./(abs(data1-a)/max(abs(data1-a)));endfunction data=qu7(data1,a,b)%区间指标1% 填7的时候选择for i=1:length(data1)if(data1(i)>a)&&(data1(i)<b)data(i)=1;elseif (data1(i)<a)data(i)=data1(i)/a;elseif (data1(i)>b)data(i)=b/data1(i);endend
end
数据清洗
缺失值处理
对于缺失值的三种处理方法:不处理,删除数据,数据插补。
数据插补的方法:
- 均值/中位数/众数插补
- 使用固定值插补
- 最近邻插补:即在记录中找到与缺失样本最接近的样本的该属性插补,可以通过计算对象间的欧式距离衡量。
- 回归方法插补:根据已有数据和与其有关的其他变量的数据建立拟合模型来预测缺失值
- 插值法插补(推荐):常用的插值法有很多,主要有拉格朗日插值法、牛顿插值法。
对于缺失值处理,我们需要分情况讨论。
如果某个变量或某个样本缺失了 70%以上的数据,那么此时对数据进行填补的话,会引入更多的噪声,反而会降低模型的性能,故此时一般直接将该变量或样本删除;
如果缺失的不多,我们可以考虑对缺失值进行填补。
matlab API:
- ismissing 或者 isnan :返回一个与输入矩阵同形状的01矩阵,1表示此位置是缺失值。
- rmmissing:直接删除缺失值所在的行列,第二个参数 1 表示行,2表示列。
- fillmissing:填补缺失值。
-
常数填充:constant
- 插值法,常见的插值方法如下:
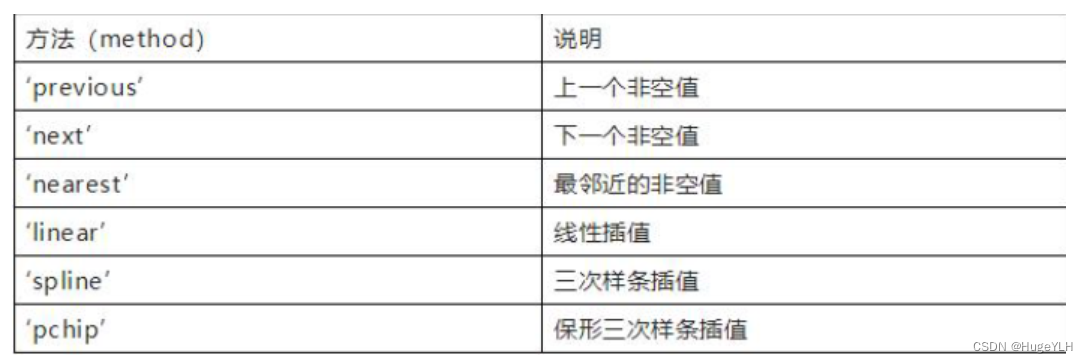
-
移动窗口填充法:该方法的思想是在缺失值前后开一个“窗口”,用“窗口”内 的数据的均值或中位数进行填充。
-
代码实现:
clc;clear;
% 数据的预处理
load("带缺少数据.mat");data = data_nan;
%% 缺失值处理
% 判断矩阵中是否存在nan值,返回一个同形状的0-1矩阵,1表示此位置是nan
nan_mat = isnan(data);
%% 直接删除空值所在的行:1
data1 = rmmissing(data); %默认为1行
%% 直接删除空值所在的列:2
data2 = rmmissing(data,2);%% 填充缺失值,插值
% 1. 常量填充缺失值
data3 = fillmissing(data,"constant",999);
%% 2. 上一个或者下一个非空值
data4 = fillmissing(data,'previous'); % next 表示以下一个非空值填充
%% 3. 最邻近的非空值
data5 = fillmissing(data,'nearest');
%% 4. 三次样条插值
data6 = fillmissing(data,'spline'); % phcip 保持三次样条插值
%% 5. 窗口填补法
data7 = fillmissing(data,'movmean',8,1); % movean 窗口长度为 window 的移动均值; movmedian:移动中位数
异常值处理
- 正态分布3σ原则:总体符合正态分布,例如人口数据、测量误差、生产加工质量、考试成绩等。
- 计算均值 μ 和标准差 σ 。
- 判断每个数据值是否在(μ-3σ,μ+3σ) 内,不在则为异常值.
- 异常值可以转换为
nan值,然后再进行上一步的缺失值处理。
- 画箱线图:下四分位数Q1是排第25%的数值,上四分位数Q3是排第75%的数值。四分位距IQR= Q3-Q1,也就是排名第75%的减去第25%的数值正态分布类似,设置个合理区间,在区间外的就是异常值。一般设[Q1−1.5IQR, Q3+1.5IQR]内为正常值。