Python解决0-1规划问题

参考下面文章

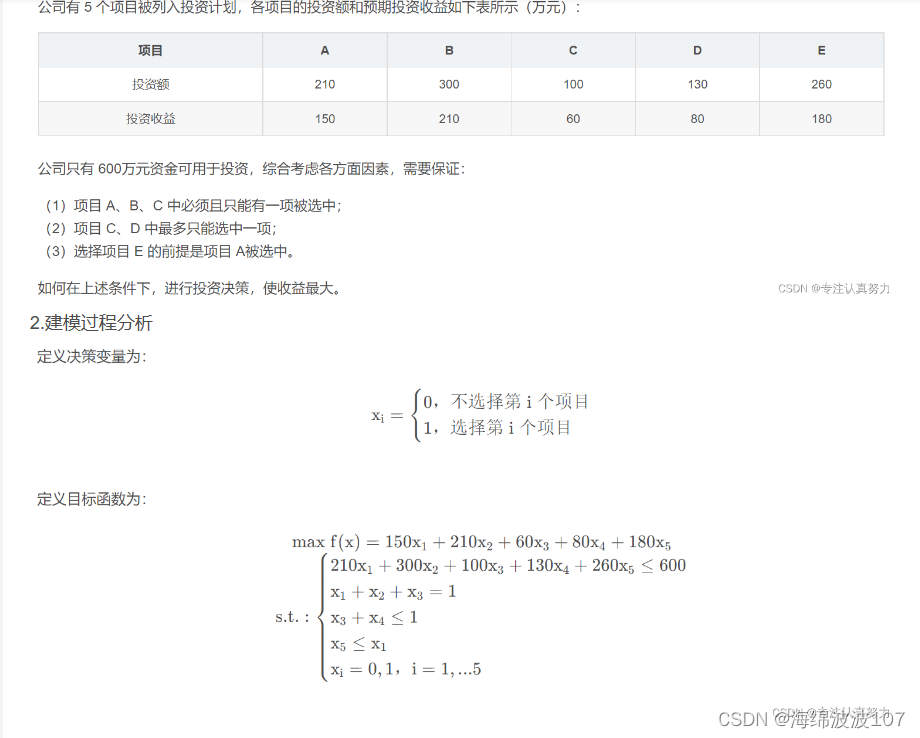
源代码

import pulp      # 导入 pulp 库# 主程序
def main():# 投资决策问题：# 公司现有 5个拟投资项目，根据投资额、投资收益和限制条件，问如何决策使收益最大。"""问题建模：决策变量：x1～x5：0/1 变量，1 表示选择第 i 个项目， 0 表示不选择第 i 个项目目标函数：max fx = 150*x1 + 210*x2 + 60*x3 + 80*x4 + 180*x5约束条件：210*x1 + 300*x2 + 100*x3 + 130*x4 + 260*x5 <= 600x1 + x2 + x3 = 1x3 + x4 <= 1x5 <= x1x1,...,x5 = 0, 1"""InvestLP = pulp.LpProblem("Invest decision problem", sense=pulp.LpMaximize)  # 定义问题，求最大值# 参数 cat 用来设定变量类型，’ Binary ’ 表示0/1变量（用于0/1规划问题）。x1 = pulp.LpVariable('x1', cat='Binary')  # 定义 x1，A 项目x2 = pulp.LpVariable('x2', cat='Binary')  # 定义 x2，B 项目x3 = pulp.LpVariable('x3', cat='Binary')  # 定义 x3，C 项目x4 = pulp.LpVariable('x4', cat='Binary')  # 定义 x4，D 项目x5 = pulp.LpVariable('x5', cat='Binary')  # 定义 x5，E 项目InvestLP += 150*x1 + 210*x2 + 60*x3 + 80*x4 + 180*x5  # 设置目标函数 f(x)InvestLP += (210*x1 + 300*x2 + 100*x3 + 130*x4 + 260*x5 <= 600)  # 不等式约束InvestLP += (x1 + x2 + x3 == 1)  # 等式约束InvestLP += (x3 + x4 <= 1)  # 不等式约束InvestLP += (x5 - x1 <= 0)  # 不等式约束InvestLP.solve()  # solve() 是求解函数，可以对求解器、求解精度进行设置。print(InvestLP.name)  # 输出求解状态print("Status youcans:", pulp.LpStatus[InvestLP.status])  # 输出求解状态for v in InvestLP.variables():print(v.name, "=", v.varValue)  # 输出每个变量的最优值print("Max f(x) =", pulp.value(InvestLP.objective))  # 输出最优解的目标函数值returnif __name__ == '__main__':main()

运行结果