整数规划

整数规划问题是优化变量必须取整数值的线性或非线性规划问题，不过，在大多数情况下，整数规划问题指的是整数线性规划问题。

其数学模型为
m i n f ( x ) = c T x s.t A x = b x ≥ 0 x i ∈ I , i ∈ I ⊂ { 1 , 2 , . . . , n } min \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t} \quad \pmb A\pmb x=\pmb b \\ \pmb x ≥ 0\\ x_i \in I, i\in I \subset\{1,2,...,n\} minf(x)=cTxs.tAx=bx≥0xi​∈I,i∈I⊂{1,2,...,n}
特别地，如果 I = { 0 , 1 } I = \{0, 1\} I={0,1}，上述模型也被称为0-1规划问题。

相比此前已经介绍的线性规划问题，整数规划问题其实就是多了组整数约束。鉴于两者如此紧密的关系，如下所示的线性规划问题被称为整数规划问题的松弛问题。
$$\begin{gathered} minf(x)=c^{T}x \\ \text{s.t}Ax=b \\ x\ge 0 \end{gathered}$$

虽然看起来只是优化变量多了组整数条件的约束，但是在理论上，整数规划问题的求解已经不再是多项式复杂度了。

目前最常用的整数规划问题求解算法有两个：割平面法和分支定界法。不用被名字吓到，它们的本质都只是在单纯形法之外再额外增加一些算法逻辑，从而保证可以取到整数解。而这些算法逻辑，更像是算法框架，通过简单的实例就能描述清楚其背后的设计思想。

割平面法

本节通过求解如下的一个整数规划问题，来说明割平面法的算法原理。
$$\begin{gathered} minz=-5x_1-8x_2 \\ \text{s.t}{x}_1+x_2+x_3=6 \\ 5x_1+9x_2+x_4=45 \\ {x}_1,x_2,x_3,x_4\ge 0,且只能取整数 \end{gathered}$$
首先计算其对应的松弛问题，得到最优解为
$$x_1=9/4,x_2=15/4$$
下图中，A点即为最优解。显然，该解并不满足优化变量为整数的约束。

此时，割平面法的思路是：先把A点附近的非整数区域从可行域中切掉，然后再重新计算最优解。“切”的数学描述可以表达为：给松弛问题增加一个约束。本实例中，约束的表达式为
$$0.75x_3+0.25x_4\ge 0.75$$
增加约束后，可行域如下图所示，重新求解得到最优解为
$$x_1=0,x_2=5$$
该解虽然是求解松弛问题得到的最优解，但由于也满足整数条件的约束，所以也自然是原整数规划的最优解。

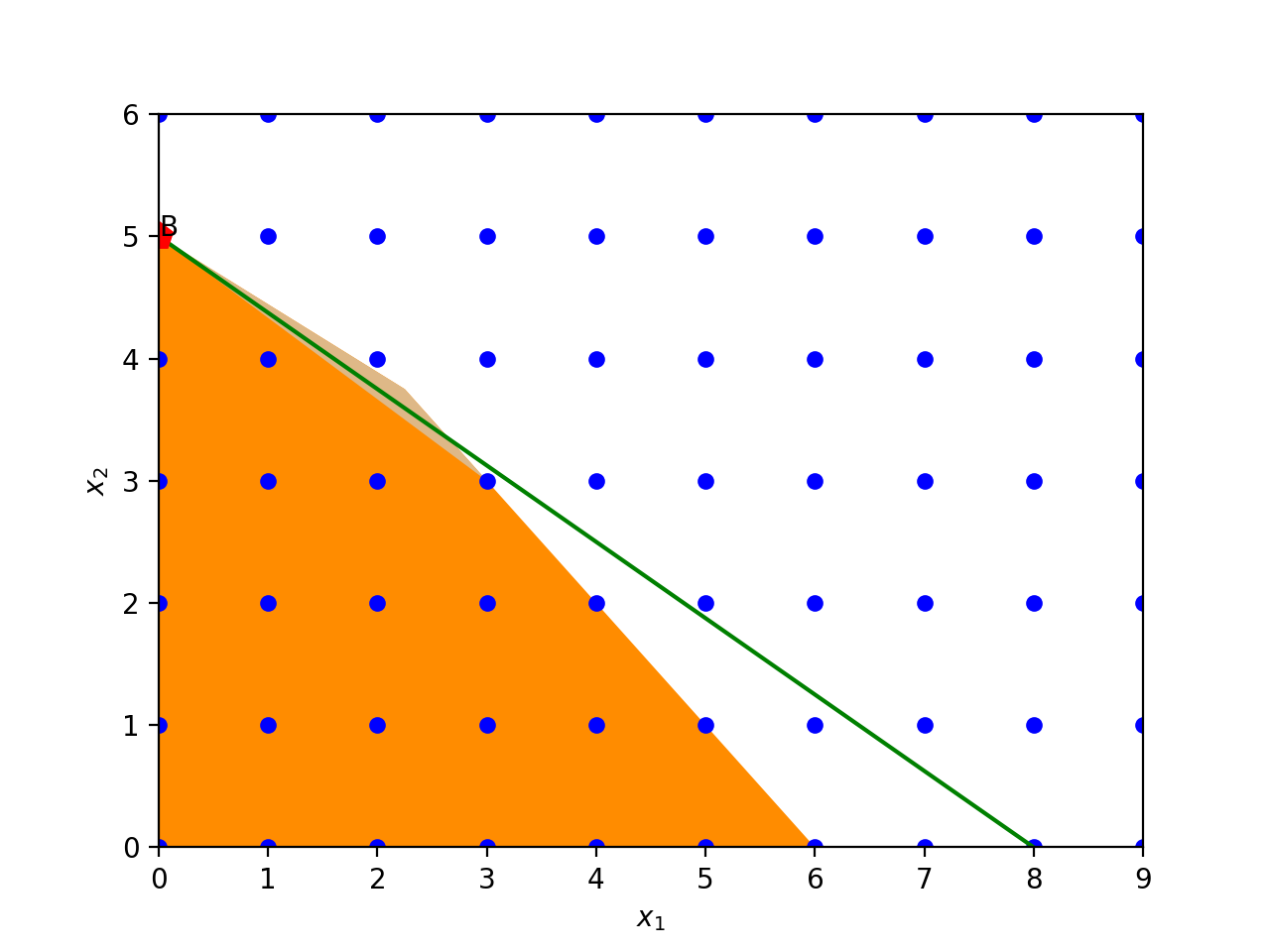
现在唯一的问题就只有：如何得到新增的约束表达式？接下来详细阐述。

切割前，最优解对应的单纯形表如下所示。单纯形表是基于单纯形法得来的，这篇文章给予了详细说明。本文不单开章节描述单纯形表的创建和迭代过程，主要是因为在实际应用时并不需要这些。

			-5	-8	0	0
C_b	基	b	x_1	x_2	x_3	x_4
-5	x_1	9/4	1	0	9/4	-1/4
-8	x_2	15/4	0	1	-5/4	1/4

从单纯形表的$x_2$那一行，可知
$$\frac{15}{4}=0x_1+1x_2-\frac{5}{4}{x}_3+\frac{1}{4}{x}_4$$
将系数的整数部分和小数部分拆开，可得
$$3+\frac{3}{4}=(0+0)x_1+(1+0)x_2+(-2+\frac{3}{4})x_3+(0+\frac{1}{4})x_4$$

合并整数和小数部分
$$(0x_1+1x_2-2x_3+0x_4-3)+(0x_1+0x_2+\frac{3}{4}{x}_3+\frac{1}{4}{x}_4)=\frac{3}{4}$$

等式左边第一项为整数部分，而等式右边为$[0,1]$的小数，所以等式左边第二项的小数部分必然大于等于右边的值，即
$$(0x_1+0x_2+\frac{3}{4}{x}_3+\frac{1}{4}{x}_4)\ge \frac{3}{4}$$
该式即刚刚我们要添加的约束。

当然了，从图上可以看出，横纵坐标是$x_1,x_2$，但是约束条件是关于$x_3,x_4$，所以要做可视化的话，还需要转换一下
$$x_3=6-x_1-x_2,x_4=45-5x_1-9x_2$$
然后代入新添加的约束，变为
$$2x_1+3x_2\le 15$$
这样就可以画出如上所示的图了。

至于为什么要选择$x_2$那一行来构造新的约束，这主要是因为，有经验表明，使用小数部分最大的那一行来构造约束，收敛会更快。

分支定界法

相比割平面法，分枝定界法的思路更容易理解。

以如下的实例为例：
$$\begin{gathered} minf(x)=-10x_1-20x_2 \\ \text{s.t}5x_1+8x_2\le 60 \\ {x}_1\le 8 \\ {x}_2\le 4 \\ {x}_1,x_2\ge 0,且只能取整数 \end{gathered}$$

(1) 定义P为原整数规划问题，P0为其对应的松弛问题，最优解为
$$x_0=(5.6,4),f_0=-136$$
由于$x_0$不满足整数约束，所以该解并不是P的最优解。但是P的最优解$f^{\ast }$肯定不会低于P0的最优解，所以$f_0$可以作为P的下界
$$f_{lb}=-136$$

此外，我们很容易发现，$x=(0,0)$是P的一个可行解，此时$f=0$，P的最优解$f^{\ast }$不会高于该值，所以P的上界是
$$f_{ub}=0$$

(2) 在P0的最优解中，由于$x_1=5.6$，引入两个互斥的约束条件：
$$x_1\le 5,x_1\ge 6$$
将这两个约束分别加入P中，得到子问题P1和P2。显然，P的最优解和P1、P2最优解的更小者相同。

求解P1对应的松弛问题，最优解为
$$x_1=(5,4),f_1=-130$$
由于$x_1$为整数解，所以也是P1的最优解，上界$f_{ub}$可以修改为
$$f_{ub}=f_1=-130$$
由于P1已经得到整数最优解，所以P1不需要再继续被分支。

求解P2对应的松弛问题，最优解为
$$x_2=(6,3.75),f_2=-135$$
$x_2$不满足整数条件，因此不是P2的最优解，但是$f^{\ast }$不会低于$f_2$，所以可以更新下界
$$f_{lb}=-135$$

(3) 在P2的最优解中，由于$x_2=3.75$，继续引入两个互斥的约束条件
$$x_2\le 3,x_2\ge 4$$
将这两个约束分别加入P2中，得到子问题P3和P4。

先求解P4对应的松弛问题，无可行解，所以可以停止分枝。

再求解P3对应的松弛问题，最优解为
$$x_3=(7.2,3),f_3=-132$$
$x_3$不满足整数条件，因此不是P3的最优解，但是$f^{\ast }$不会低于$f_3$，所以可以继续更新下界
$$f_{lb}=-132$$

(4) 在P3的最优解中，由于$x_1=7.2$，继续引入两个互斥的约束条件
$$x_1\le 7,x_1\ge 8$$
将这两个约束分别加入P3中，得到子问题P5和P6。

求解P5对应的松弛问题，最优解为
$$x_5=(7,3),f_5=-130$$
由于$x_5$为整数解，所以也是P5的最优解，上界$f_{ub}$可以修改为
$$\overline{f}=f_5=-130$$
此时，P5不需要再继续被分支。

求解P6对应的松弛问题，最优解为
$$x_6=(8,2.5),f_6=-130$$
$x_6$不满足整数条件，但是$f_6$并不小于当前上界$f_{ub}$，所以该分支是“枯枝”，需要剪枝。

结合P5和P6，下界可以更新为
$$f_{lb}=-130$$

此时，我们发现
$$f_{ub}=f_{lb}=-130$$
所以该问题的最优解为
$$x_1=(5,4)或x_5=(7,3)$$
对应的目标函数值为
$$f^{\ast }=-130$$

分支定界的全过程可以参考下图。

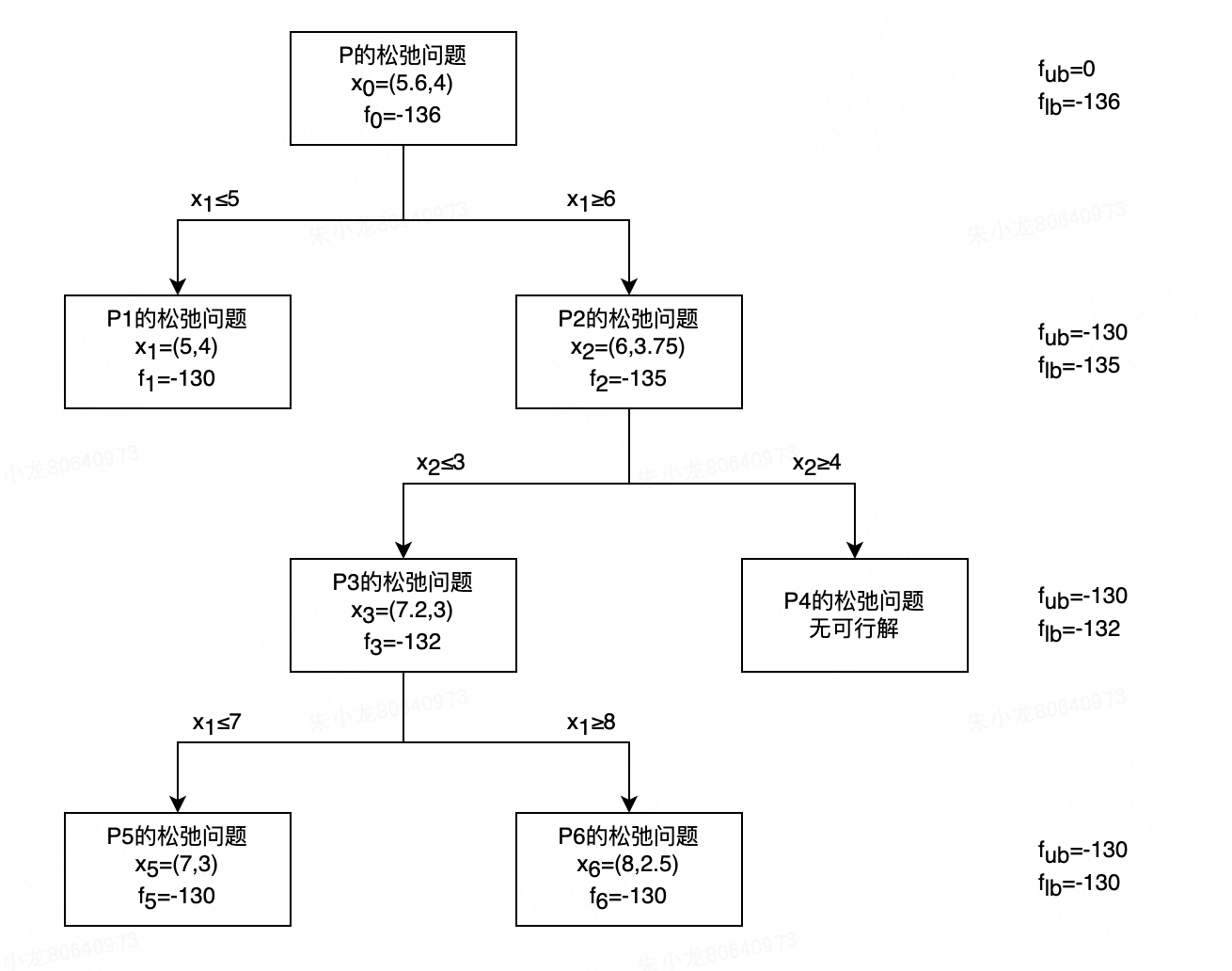
总的来说，割平面法和分支定界法都是先计算原问题对应的松弛问题，然后判断松弛问题的最优解是否也满足整数约束，如果满足，那么皆大欢喜；反之，割平面法会通过增加约束的方式来改进松弛问题的可行域，以期达到松弛问题最优解亦为原问题最优解的目标；而分支定界法则利用分解技术，将原问题分解为若干个子问题并分别计算，然后基于子问题的求解结果持续更新原问题的上下界，直至两者相等。

代码实现

虽然割平面法和分支定界法的步骤看起来挺多的，但好在，求解器已经帮我们做好了集成的工作，所以我们可以直接调用现成的求解器来求解所遇到的整数规划问题。

基于Python调用ortools求解整数规划问题的代码，和此前介绍的线性规划代码的唯一不同点在于：整数规划中优化变量的定义是solver.IntVar，而线性规划中的定义方式是solver.NumVar。

以下是上一节整数规划问题的求解代码。

from ortools.linear_solver import pywraplpif __name__ == '__main__':# 声明ortools求解器，使用SCIP算法solver = pywraplp.Solver.CreateSolver('SCIP')# 优化变量x1 = solver.IntVar(0, 8, 'x1')x2 = solver.IntVar(0, 4., 'x2')# 目标函数solver.Minimize(-10 * x1 - 20 * x2)# 约束条件solver.Add(5 * x1 + 8 * x2 <= 60)# 模型求解status = solver.Solve()# 模型求解成功, 打印结果if status == pywraplp.Solver.OPTIMAL:# 变量最优解print('x1: {}, x2: {}'.format(x1.solution_value(), x2.solution_value()))# 最优目标函数值print('best_f =', solver.Objective().Value())else:print('not converge.')

运行代码后，可以得到最优解如下。显然，该解和上一节推演的结果是一致的。

x1: 5.0, x2: 4.0
best_f = -129.99999999999997