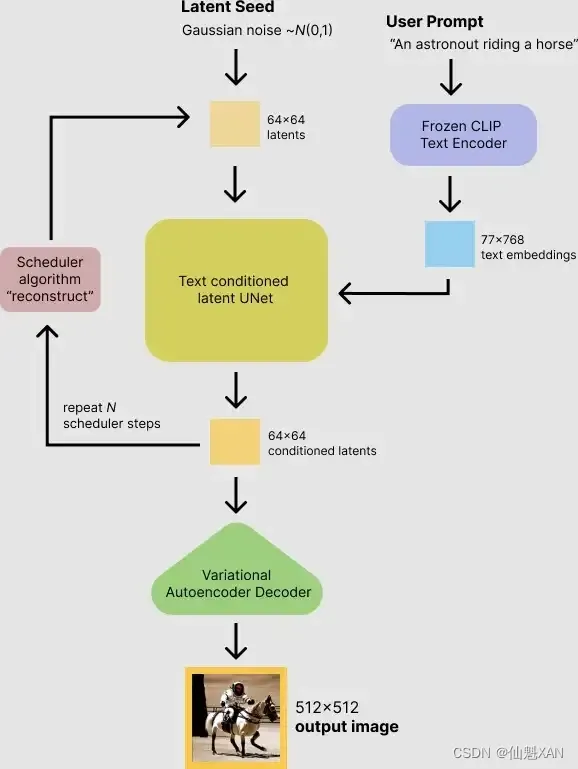
储备知识
GA算法主要解决数学模型中最优化的搜索算法,是进化算法中的一种,基因算法借鉴了自然界基因的遗传的主要现象,分别为遗传,变异,自然选择,杂交等。
GA算法参数
GA算法的参数如下所示。
- 种群规模(即一般为行数,即为个体数量)
- 字符串长度(会将一个变量编码成字符串,一般为0-1二进制字符串)
- 交配(杂交)概率(让适应度高的个体产生后代变量的概率更大,但其他个体的概率为非负数)
- 突变概率(让个体基因存在一定的突变概率,一般为1e-3)
- 终止条件,一般的终止条件如下所示。
- 循环迭代产生基因的次数
- 计算资源使用殆尽
- 已经找到全局最优质值
- 一定人为干预
GA算法的流程
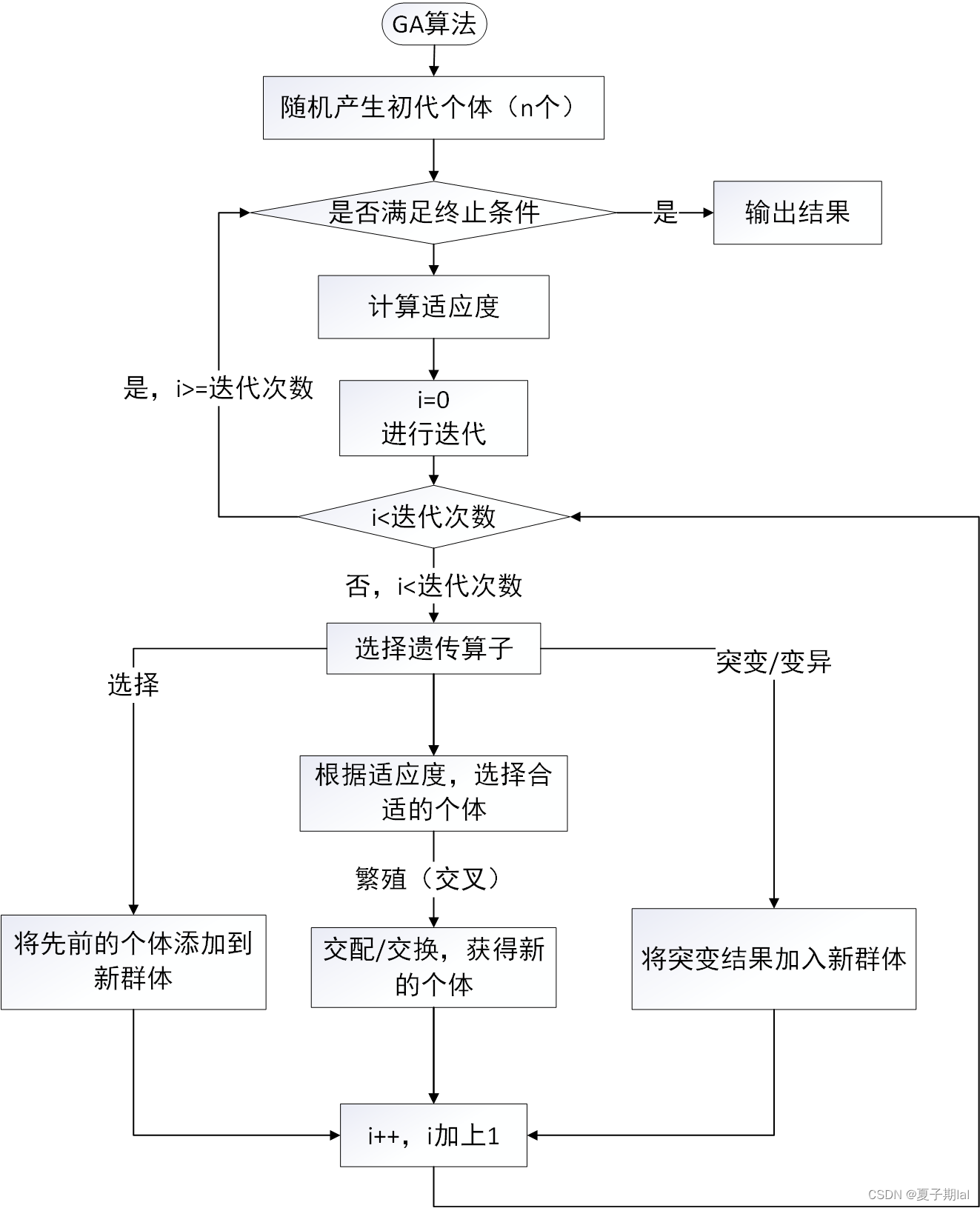
GA算法最重要的为适应度函数以及自变量的取值范围,以及变量的个数,因此代码实现流程如下所展示。
- 算法随机生成一定数量的个体,生成初始种群的质量
- 对每一代评价每个个体,确定适应度数值
- 产生下一代,这过程包括交叉操作以及突变操作。一般按照适应度数值排序,但不完全以适应度高地为导向,因为有可能造成局部最优解。
- 继续循环2-3的步骤,直到满足终止条件(上述已经说明)
具体流程如图所示。
GA算法的适应度函数
适应度函数一般都是用目标函数确定的。目标函数即为因变量与自变量之间的映射函数。而适应度函数主要目的是确定优化的方向,即为最小化还是最大化目标函数值。最小化最大化的代码如下所示。
def Function_(x, y): # Function_(x, y)为目标函数pass
def get_fitness(pop, type='min'):
# get_fitness(pop, type='min')为自适应函数,一般为确定min为追求最小化,max为追求最大化
# x,y的参数主要根据目标函数的自变量个数去确定if type is 'min':x,y = translateDNA(pop)pred = Function_(x, y)return -(pred - np.max(pred)) + 1e-3elfi type is 'max':x,y = translateDNA(pop)pred = Function_(x, y)return (pred - np.min(pred)) + 1e-3
GA算法的编码
此外在运用遗传算法的时候,最重要的是会将自变量编码为我们所需要的字符串,这个过程称之为编码,编码方式为二进制编码,将十进制的数字转化为二进制,如5编码之后变成101。后续编码会将补全到某个特定的二进制编码,如变成0000000101(10位二进制编码)。
GA算法的遗传因子选择
选择
交叉
变异
代码实现过程
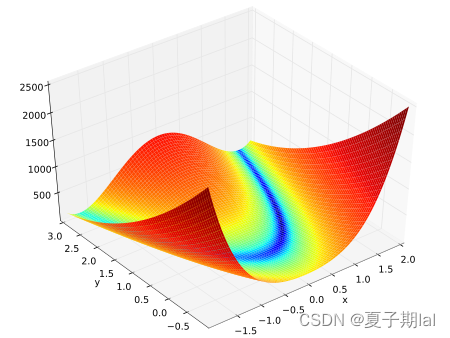
具体问题具体分析,文中主要以Rosenbrock函数的极大值为例子(参考了知乎某位大佬的例子遗传算法python(含例程代码与详解))
该函数又称为香蕉函数。具体如图所示。
具体的函数解析式如下所示。
f ( x , y ) = ( 1 − x ) 2 + 100 ( y − x 2 ) 2 . f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}. f(x,y)=(1−x)2+100(y−x2)2.
代码
import numpy as np
import matplotlib.pyplot as plt# 适应度函数,求取最大值
#因为GA函数是求最小值,所以我在适应度函数上加一个负号
#GA要求输入维度2维及其以上,所以我传入2个参数,第二维x2不用,
def fitness(y, x):# x1, x2 = x# return -(x1 + 16 * np.sin(5 * x1) + 10 * np.cos(4 * x1))return -(100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0)# 个体类
from sko.GA import GA
up_bound = [2.048, 2.048]
low_boound = [-2.048, -2.048]
n_dim = 2
iter_num = 800
precision = 1e-7
size_pop = 50
ga = GA(func=fitness, n_dim=n_dim, size_pop=size_pop, max_iter=iter_num, lb=low_boound, ub=up_bound, precision=precision)
# 具体代码的修改需要根据n_dim以及lb和ub的个数,个人理解lb是下限,ub为上限,此外,修改为适应度函数的时候需要注意,即为修改以及调整适应度函数的自变量个数以及表达式
best_x, best_y = ga.run()
# best_x 输出的是坐标,所以就是为一个元组,best_y为因变量,所以输出是一个数值
print('best_x:', best_x[0], '\n', 'best_y:', -best_y)def func(y, x):# return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)return 100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0# 绘制二维图像
# x = np.linspace(-10, 10, 100000)
# y = func(x)
#
# plt.plot(x, y)
# plt.scatter(best_x[0], -best_y, c='r', label='best point')# 绘制三维图像
ax3 = plt.axes(projection='3d')
X = np.linspace(low_boound[0], up_bound[0], 100)
Y = np.linspace(low_boound[1], up_bound[1], 100)
X, Y = np.meshgrid(X, Y)
Z = 100.0 * (Y - X ** 2.0) ** 2.0 + (1 - X) ** 2.0
# plt.scatter(best_x[0], best_x[1], -best_y, c='r', label='best point')
ax3.scatter(best_x[0], best_x[1], -best_y, c='r', label='best point')
ax3.plot_surface(X, Y, Z, cmap='rainbow')
# # ax3.contour(X, Y, Z, zdim='z',offset=-2, cmap='rainbow') #等高线图,要设置offset,为Z的最小值
plt.legend()
plt.show()
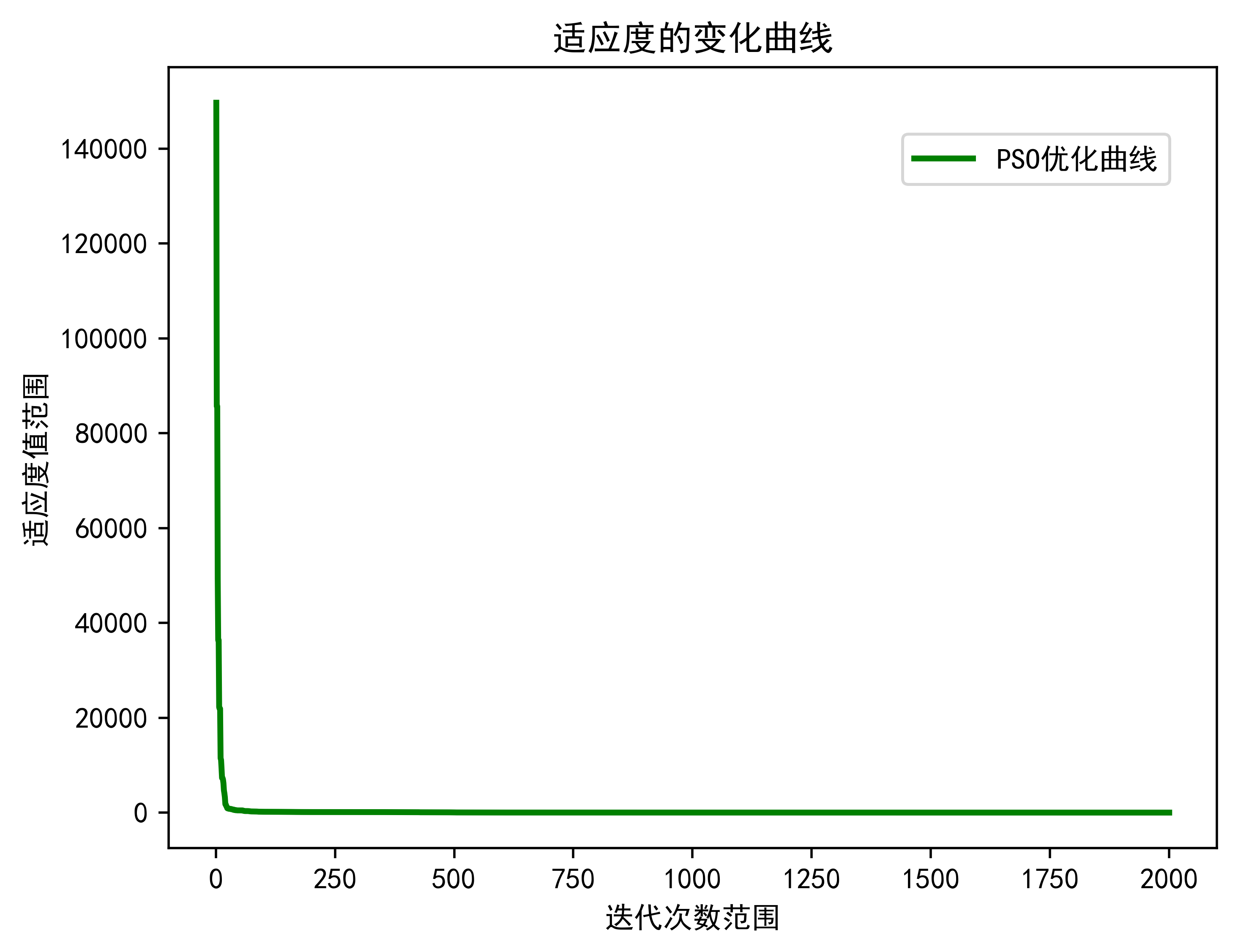
最终绘制结果如下所示。

参考
维基百科遗传算法介绍
matlab遗传算法介绍——寻找高度非线性问题的全局极小值
遗传算法python(含例程代码与详解)(知乎)
遗传算法python进阶理解+论文复现(纯干货,附前人总结引路)