Halo,这里是Ppeua。平时主要更新C++,数据结构算法,Linux与ROS…感兴趣就关注我bua!
文章目录
- 0. 题目解析
- 1. 算法原理
- 1.1 状态表示
- 1.2 状态转移方程
- 1.3初始化
- 1.4 填表顺序
- 1.5 返回值
- 2.算法代码

🐧 本篇是整个动态规划的入门篇章,题目或许可以通过暴力或者其他方法求解但在这里,我们只讨论与动态规划相关的解法.
🐧 Gitee链接:面试题 08.01. 三步问题
0. 题目解析
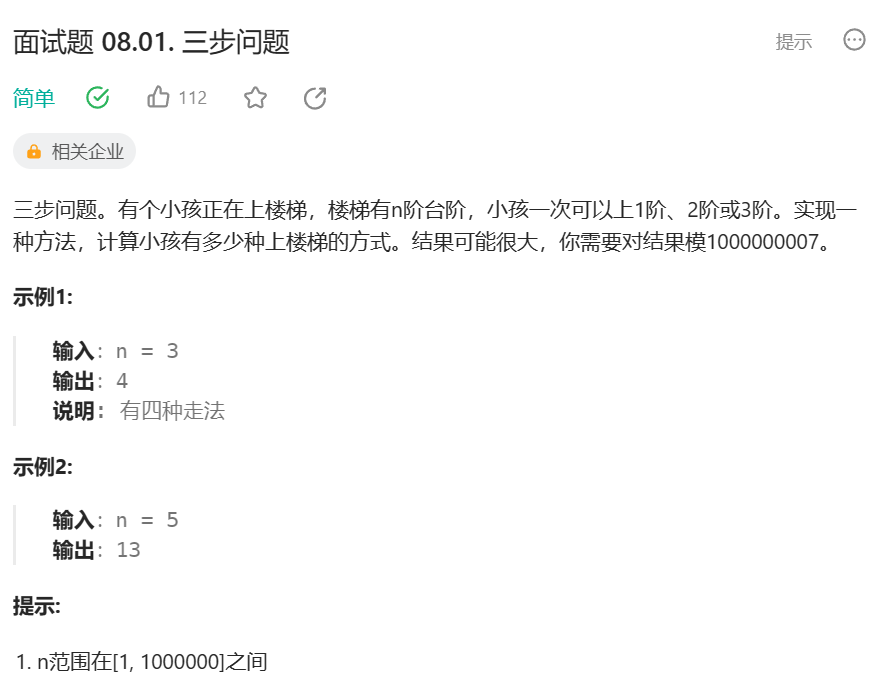
题目链接:面试题 08.01. 三步问题
一个小孩一次能上1,2,3层阶梯,求解到n阶台阶时有多少种走法。
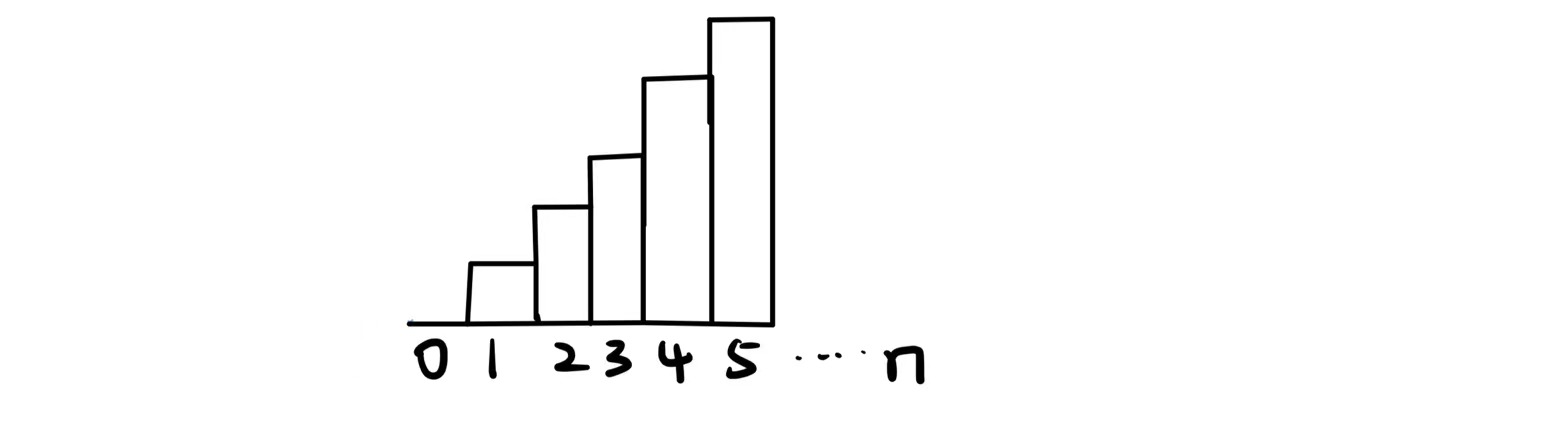
1. 算法原理
每个动态规划问题我们都会按照如下方法去分析.
1.1 状态表示
也就是dp数组(也称dp表)中,dp[i]所代表的意思是什么?
这个状态表示怎么来的?
-
分析题目的要求得出来的----按照这题为例 dp[i]等于 走到第n个台阶时所有的走法
-
根据以往做题的经验+题目的要求得出来的(这个我们之后会用到)
-
分析问题中发现重复的子问题 (较难的dp问题的状态表示往往由若干个子状态一起表示)
1.2 状态转移方程
这也就是如何求出dp[i]

我们观察发现,dp[i]可以由前三个台阶推出来.
例如:到台阶4的时候,可以由台阶一,台阶二,台阶三的步数走出来
具体的如下:可以由台阶1跳三格,台阶2跳两格,台阶3跳一格走到(注意这是一次跳的,而不是总共完成这么多格,所以只会有一种方法而不是多种)
所以如果我想要到台阶4的方法数就等于由台阶1的方法数+台阶2的方法数+台阶3的方法数.
所以dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
1.3初始化
核心思想为:保证数组不越界的情况下,完成我们的状态转移方程.
观察我们的状态转移方程,我们会发现,我们需要的值是i的前三个(i-1,i-2,i-3).所以当i=3时,最小位(i-3)此时为0.
这意味着:我们要保证不越界,我们的dp表要从i=3开始填,也就是i=0、1、2都已经初始化完
结合题目所给条件,我们不难发现:

所以初始化为:dp[0]=0,dp[1]=1,dp[2]=2
注意,当题目所给n的范围小于2时,我们访问dp[2]会造成越界.所以需要特判一下
1.4 填表顺序
为了保证填写当前状态的时候,所需要的状态已经计算过了,我们从左向右填
1.5 返回值
根据我们的dp[i]表示走到第i个台阶的方法数,而题目要求我们返回 走到第n个台阶的方法数,所以我们直接返回dp[n]即可
2.算法代码
class Solution {
int N=1000000007;
public:int waysToStep(int n) {vector<int>dp(n+1,0);if(n==1||n==2)return n;dp[0]=0,dp[1]=1,dp[2]=2,dp[3]=4;//o(n)时间复杂度 o(n)时间复杂度for(int i=4;i<=n;i++){dp[i]=((dp[i-1]%N+dp[i-2])%N+dp[i-3]%N)%N;}return dp[n];}
};
时间复杂度:o(n)
空间复杂度:o(n)
可以使用滚动数组的方法将空间复杂度优化到o(1)级别.
观察状态转移方程.我们发现,虽然我们开辟了n个大小的空间,但我们计算第i个的时候,只会用到前三个的值,这意味着在[0,i-4]这段区间中的数组空间都是浪费的.所以我们可以单独创建三个变量来表示所需要的状态值,来取代这个数组,从而优化空间复杂度.
空间,但我们计算第i个的时候,只会用到前三个的值,这意味着在[0,i-4]这段区间中的数组空间都是浪费的.所以我们可以单独创建三个变量来表示所需要的状态值,来取代这个数组,从而优化空间复杂度.