目录
120.三角形最小路径和
64.最小路径和
63.不同路径Ⅱ
5.最长回文子串
120.三角形最小路径和
题意:
给定一个三角形
triangle,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标
i,那么下一步可以移动到下一行的下标i或i + 1。
【输入样例】triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
【输出样例】11
解题思路:
1. 定义一个新的二维list,list[j][i]表示在第j行中,下标为i处得到的最小路径和为多少
2. 边遍历triangle边计算,直到整个triangle遍历完毕,输出最后一行的最小值即可
3. 动态规划的规律,是triangle[j][i] += min(list[j-1][i-1],list[j-1][i]),初始是list[0][0]=triangle[0][0];
class Solution {public int minimumTotal(List<List<Integer>> triangle) {int len = triangle.size();//共有多少行;int[][] list = new int[len][len];list[0][0] = triangle.get(0).get(0);for(int j = 1;j < len; ++j){list[j][0] = triangle.get(j).get(0)+list[j-1][0];for(int i= 1; i < j; ++i){//普通情况list[j][i] = triangle.get(j).get(i)+Math.min(list[j-1][i-1],list[j-1][i]);}list[j][j] = triangle.get(j).get(j)+list[j-1][j-1];}int result = Integer.MAX_VALUE;for(int i = 0;i< len;++i){result = Math.min(result,list[len-1][i]);}return result;}
}时间: 击败了77.67%
内存: 击败了42.52%
64.最小路径和
题意:
给定一个包含非负整数的
m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
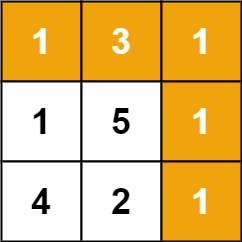
【输入样例】grid = [[1,3,1],[1,5,1],[4,2,1]]
【输出样例】7
解题思路:
1. 定义一个新的二维list,list[i][j]表示在第i行中第j列得到的最小路径和是多少
2. 边遍历grid边计算,直到整个grid遍历完毕,输出list[m-1][n-1]即可
3. 动态规划的规律,是list[i][j] = grid[i][j] + Math.min(list[i-1][j],list[i][j-1]);
4. 动态规划的初始化,只能向下或向右走,那么第一行,第一列的值是固定的,list[0][0] = grid[0][0]; list[0][j] = list[0][j-1]+grid[0][j]; list[i][0] = list[i-1][0]+grid[i][0]
class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] list = new int[m][n];list[0][0] = grid[0][0];for(int i=1;i<m;++i){//第一列赋值list[i][0] = list[i-1][0] + grid[i][0];}for(int j=1;j<n;++j){//第一行赋值list[0][j] = list[0][j-1] + grid[0][j];}for(int i = 1; i< m; ++i){for(int j = 1; j < n; ++j){list[i][j] = grid[i][j] + Math.min(list[i-1][j],list[i][j-1]);}}return list[m-1][n-1];}
}时间: 击败了93.62%
内存: 击败了18.20%
63.不同路径Ⅱ
题意:
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。
【输入样例】obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
【输出样例】2
解题思路:
1. 定义一个新的二维list,list[i][j]表示走到第i行中第j列的路径数
2. 边遍历obstacleGrid边计算,直到整个obstacleGrid遍历完毕,输出list[m-1][n-1]即可
3. 动态规划的规律,是当obstacleGrid[i][j] == 0时 list[i][j] = list[i-1][j]+list[i][j-1];路径数要相加,
如果obstacleGrid[i][j]==1 ,将list[i][j] 赋值为0
4. 动态规划的初始化,list[0][0] = 1; 只能向下或向右走,那么第一行,第一列的值是固定的,如果说第一行和第一列没有障碍,全部都为1,如果存在障碍,障碍之后的都为0.
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] list = new int[m][n];if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1){return 0;}list[0][0] = 1;for(int i=1;i<m && obstacleGrid[i][0] == 0;++i){//开始判断第一列的初始值list[i][0] = 1;}for(int j=1;j<n && obstacleGrid[0][j] == 0 ;++j){//开始判断第一行的初始值list[0][j] = 1;}//开始剩余格子的路径数for(int i=1;i < m; ++i){for(int j=1; j < n; ++j){list[i][j] = obstacleGrid[i][j] == 1 ? 0 : list[i-1][j]+list[i][j-1];}}return list[m-1][n-1];}
}时间: 击败了100.00%
内存: 击败了29.85%
5.最长回文子串
题意:
给你一个字符串
s,找到s中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
【输入样例】s="babad"
【输出样例】"bab" 或 "aba"
解题思路:
这题,嗯,做不太出来,参考了官方解题
自己就是把理解的地方多写了一点备注
class Solution {public String longestPalindrome(String s) {int len = s.length();if(len < 2){return s;}int maxLen = 1;int begin = 0;//dp[i][j]表示s[i..j]是否是回文串boolean[][] dp = new boolean[len][len];//初始化,所有长度为1的字串都是回文串for(int i=0; i<len; ++i){dp[i][i] = true;}char[] charArray = s.toCharArray();//先枚举字串长度for(int L = 2; L <= len; L++){//枚举左边界for(int i=0; i< len; ++i){//由L和i确定右边界,即j-i+1=Lint j = L + i - 1;//如果右边界越界,就可以退出当前循环if(j >= len){break;}if(charArray[i] != charArray[j]){dp[i][j] = false;}else{if(j-i < 3){//这种情况一定是回文串//j-i=0,表示只有一个字符x//j-i=1,两个字符xx,这里已知相等//j-i=2,三个字符,已知最左和最右相等,中间无所谓,即xyxdp[i][j] = true;}else{//此时其是不是回文串,取决于中间部分是不是回文串dp[i][j] = dp[i+1][j-1];}}if(dp[i][j] && j-i+1>maxLen){maxLen = j-i+1;begin = i;}}}return s.substring(begin,begin+maxLen);}
}时间: 击败了22.23%
内存: 击败了30.02%