matlab函数 能控性矩阵ctrb、能控标准型canon、零极点配置place
第一章,线性定常系统
ss
如果已知线性定常系统的ABCD四个矩阵,可以得到状态空间系统
其他更具体的用法请直接看帮助文档。
用法:ss(A,B,C,D)
假如
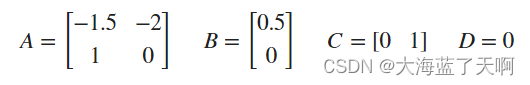
可以输入
A = [-1.5,-2;1,0];
B = [0.5;0];
C = [0,1];
D = 0;
sys = ss(A,B,C,D)
最后得到

ctrb和rank
判断系统是否能控,可以用能控性矩阵是否奇异进行判断。ctrb函数用来生成能控性矩阵,rank用来判断矩阵的秩
对于线性定常系统
x ˙ = A x + B u \dot{x}=Ax+Bu x˙=Ax+Bu
如果能控性矩阵
C O = [ B A B A 2 B ⋯ A n − 1 B ] CO=[B\ \ AB\ \ A^2B\ \ \cdots\ \ A^{n-1}B] CO=[B AB A2B ⋯ An−1B]
的行秩=n,则意味着该系统完全能控(为什么是行秩呢,因为对于MIMO系统能控性矩阵不一定是方阵)
在matlab中,可以用ctrb(A,B)直接得到能控性矩阵
比如,我事先输入矩阵A和B

再输入函数
ctrb(A,B)
就会得到能控性矩阵

也可以直接用上一个函数ss生成的状态空间系统(和上个例子所用数据不同)
A = [-1.5,-2;1,0];
B = [0.5;0];
C = [0,1];
D = 0;
sys = ss(A,B,C,D)
Co=ctrb(sys)

最后用rank(Co)计算一下能控性矩阵的秩。
比如对于这个能控性矩阵,其行秩为1,显然系统不能控

canon
要会这个函数,首先去看一下本篇第一个函数ss
状态空间方程化为高阶微分方程的实现方法是非唯一的,我们就提出了标准型便于我们研究和交流。
标准型有很多种。matlab中的标准型是第一能控标准型
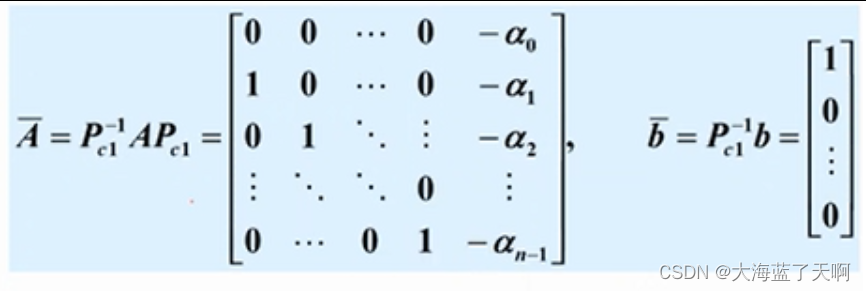
用法canon(sys,‘companion’)
比如对于这个系统

把ABCD全都输进去,然后
sys=ss(A,B,C,D)
得到

再输入canon
canon(sys,'companion')
得到

place或acker
设计全状态反馈控制律中,我们把配置闭环系统极点的过程称之为极点配置。可以用place函数(acker函数可以实现)
- 先在matlab中输入矩阵A和B
- 再输入想要的极点 P = [ 第一个 第二个 第三个 … ] P=[第一个\ \ 第二个\ \ 第三个\dots] P=[第一个 第二个 第三个…]
- 最后
acker[A,B,P] //或者用place[A,B,P]也可以,计算精度不同
- 输出的结果就是反馈矩阵K或说R
例子:
A = [-1,-2;1,0];
B = [2;0];
p = [-1,-2];
K = place(A,B,p);
得到

pole
计算系统极点。也要看本章第一个函数ss
A = [-1,-2;1,0];
B = [2;0];
C = [0,1];
D = 0;
sys = ss(A,B,C,D);
pole(sys)