- 点四叉树是一种用于主要是针对空间点存储与索引的树形数据结构
- 在点四叉树中,空间被分割成四个矩形,四个不同的多边形对应于SW、NW、SE、NE四个象限
1 基本操作
1.1 初始化
创建一个根节点,该节点代表整个二维空间区域
1.2 插入点
- 当一个新点需要被插入
- 从根节点开始,根据点的坐标确定它应该属于哪个象限,并递归地进入该象限。
- 对于k维数据空间而言,以新插入的点为中心将其对应索引空间分为两两不相交的2k个子空间,依次与它的2k个孩子结点相对应,对于位于某一子空间的点,则分配给对应的子树
- 从根节点开始,根据点的坐标确定它应该属于哪个象限,并递归地进入该象限。
1.3 查询
查询一个区域内的所有点时,从根节点开始,检查该区域与每个节点(象限)的交集,并递归地进入与查询区域有交集的节点。
2 举例
假设我们有一个二维空间,范围是[0, 16) x [0, 16),我们要插入以下几个点:
- A(2, 3)
- B(4, 7)
- C(14, 14)
- D(9, 4)
2.1 初始化
初始时,有一个[0, 16) x [0, 16)的正方形作为根节点
2.2 插入点
2.2.1 插入A:
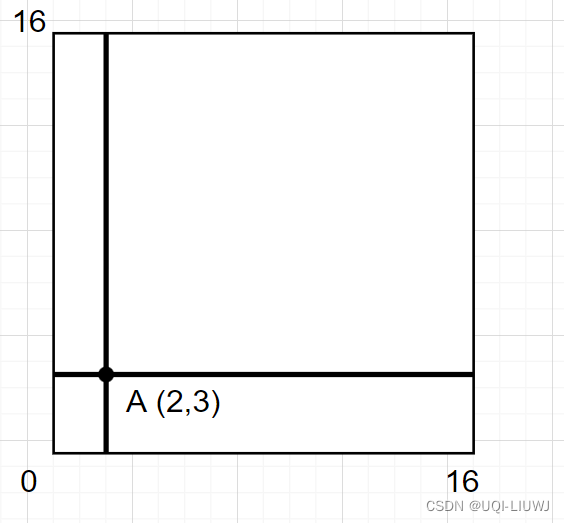
2.2.2 插入B:
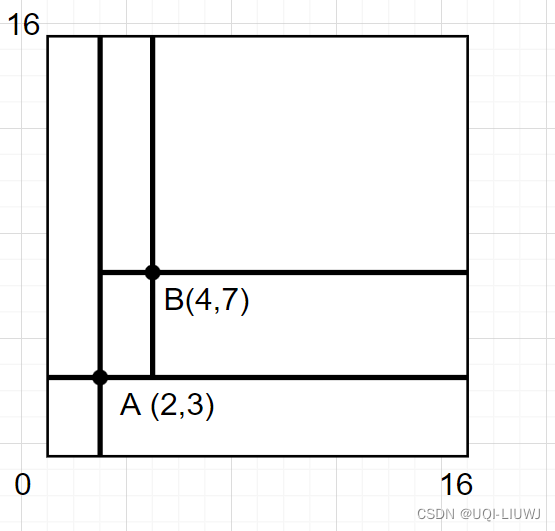
2.2.3 插入C:

2.2.4 插入D
D在以B为中心的右下方,不用再分割空间
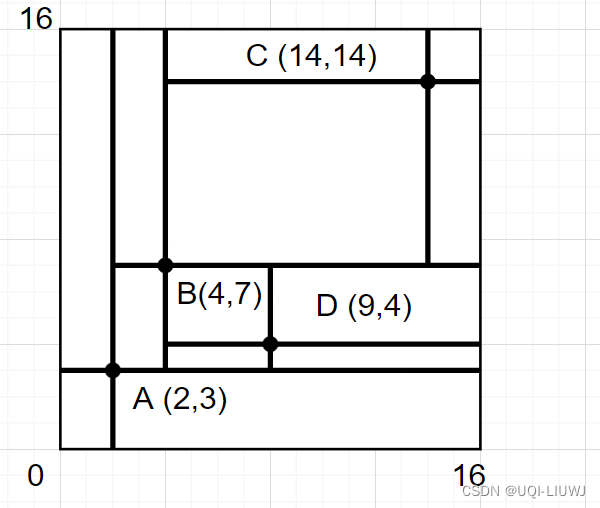
2.2.5 建树

3 优缺点
3.1 优点
- 结构简单
- 对于精确匹配的点查找性能较高
3.2 缺点
- 树的动态性差,删除结点处理复杂
- 比如上面例子中删除B点之后,应该是C还是D跟上去?如果C,D还有子节点呢?
- 每一个节点除了存储有子节点的信息外,还需要存很多的空指针
- 比如上面A点,除了存储B外,其他三个象限还需要存空指针
- ——>空间存储开销大,空间利用率第
- 比如上面A点,除了存储B外,其他三个象限还需要存空指针