组合+并集问题汇总：

1、子集去重版本
2、组合非去重版本
3、子集非去重版本

题目

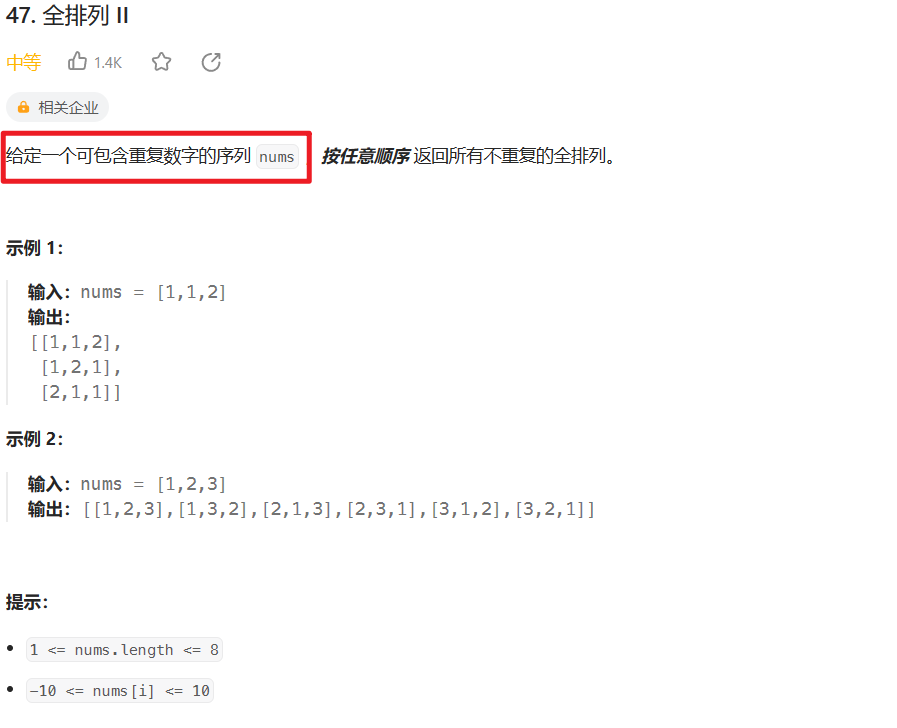相比较46题：不需要去重：【LeetCode-中等题】46. 全排列

需要做出的改变就是：

1. 首先需要对待全排列的数组进行排序（为去重操作做准备）

 Arrays.sort(nums);//对数组进行排序   方便后续进行去重操作

2. 在每次进行递归的时候，不仅需要判断标志数组是否为true（跳过此次），还要在i>0的，并且后一个位置的元素如果和前面一个元素相同，并且标志位为false（代表未处理），那么也跳过此次递归，
   

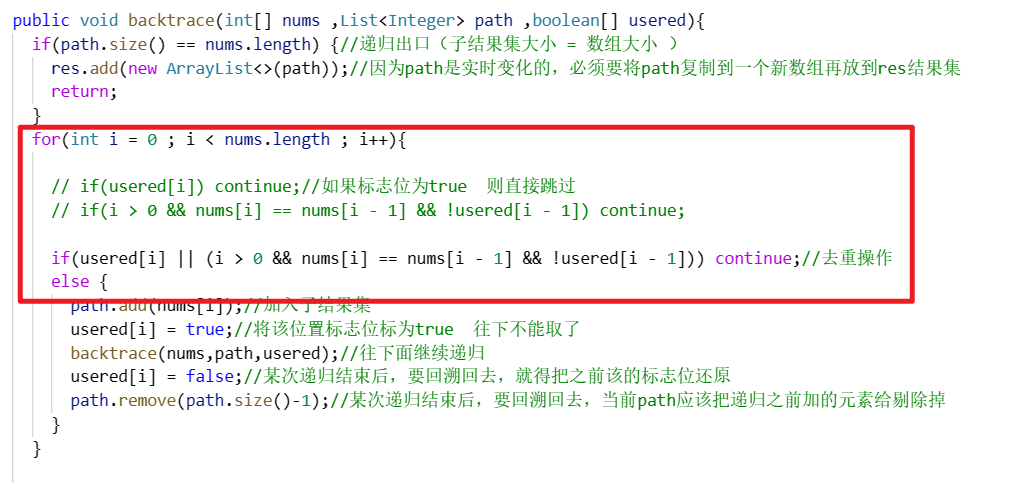
3. 最后同样是递归和回溯（和不去重的代码一样）
   
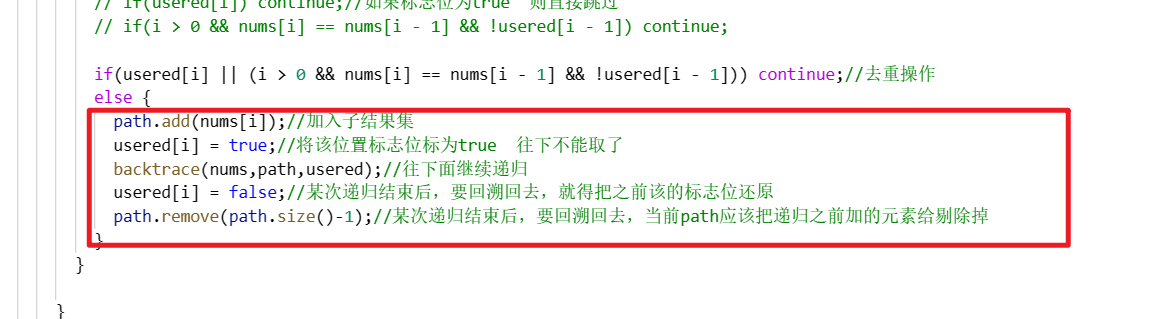
   参考视频讲解：回溯算法求解全排列，如何去重？| LeetCode：47.全排列 II
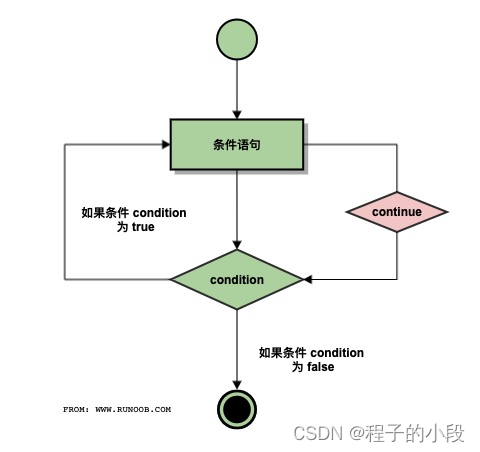
   图解全排列无去重版本：【LeetCode-中等题】46. 全排列 —无去重

方法一：递归+回溯+去重

class Solution {List<List<Integer>> res = new ArrayList<>();//最后的结果集public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);//对数组进行排序   方便后续进行去重操作List<Integer> path = new ArrayList<>(); //子结果集boolean[] usered = new boolean[nums.length]; //标记数组backtrace(nums,path,usered);return res;}public void backtrace(int[] nums ,List<Integer> path ,boolean[] usered){if(path.size() == nums.length) {//递归出口（子结果集大小 = 数组大小 ）res.add(new ArrayList<>(path));//因为path是实时变化的，必须要将path复制到一个新数组再放到res结果集return;}for(int i = 0 ; i < nums.length ; i++){// if(usered[i]) continue;//如果标志位为true  则直接跳过// if(i > 0 && nums[i] == nums[i - 1] && !usered[i - 1]) continue;if(usered[i] || (i > 0 && nums[i] == nums[i - 1] && !usered[i - 1])) continue;//去重操作else {path.add(nums[i]);//加入子结果集usered[i] = true;//将该位置标志位标为true  往下不能取了backtrace(nums,path,usered);//往下面继续递归usered[i] = false;//某次递归结束后，要回溯回去，就得把之前该的标志位还原path.remove(path.size()-1);//某次递归结束后，要回溯回去，当前path应该把递归之前加的元素给剔除掉}}}
}