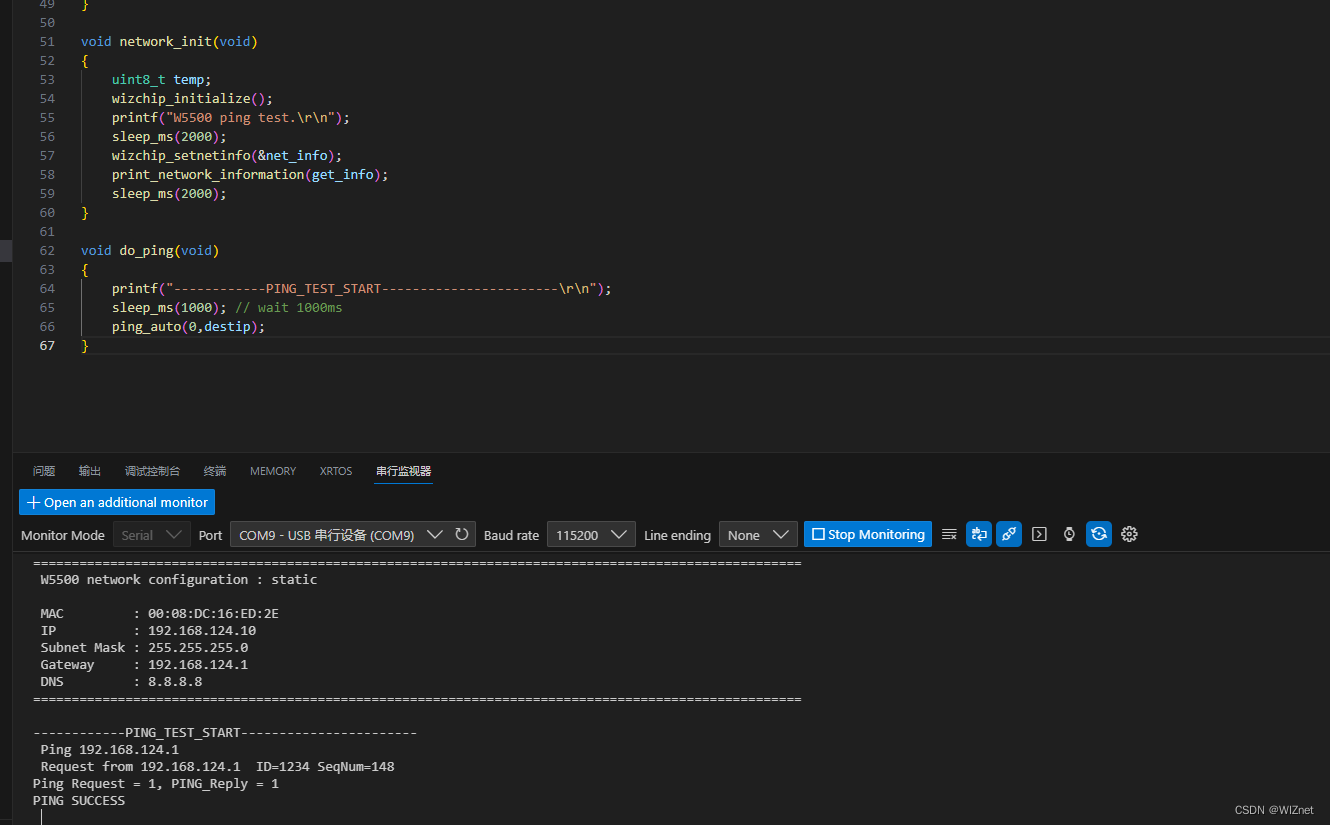
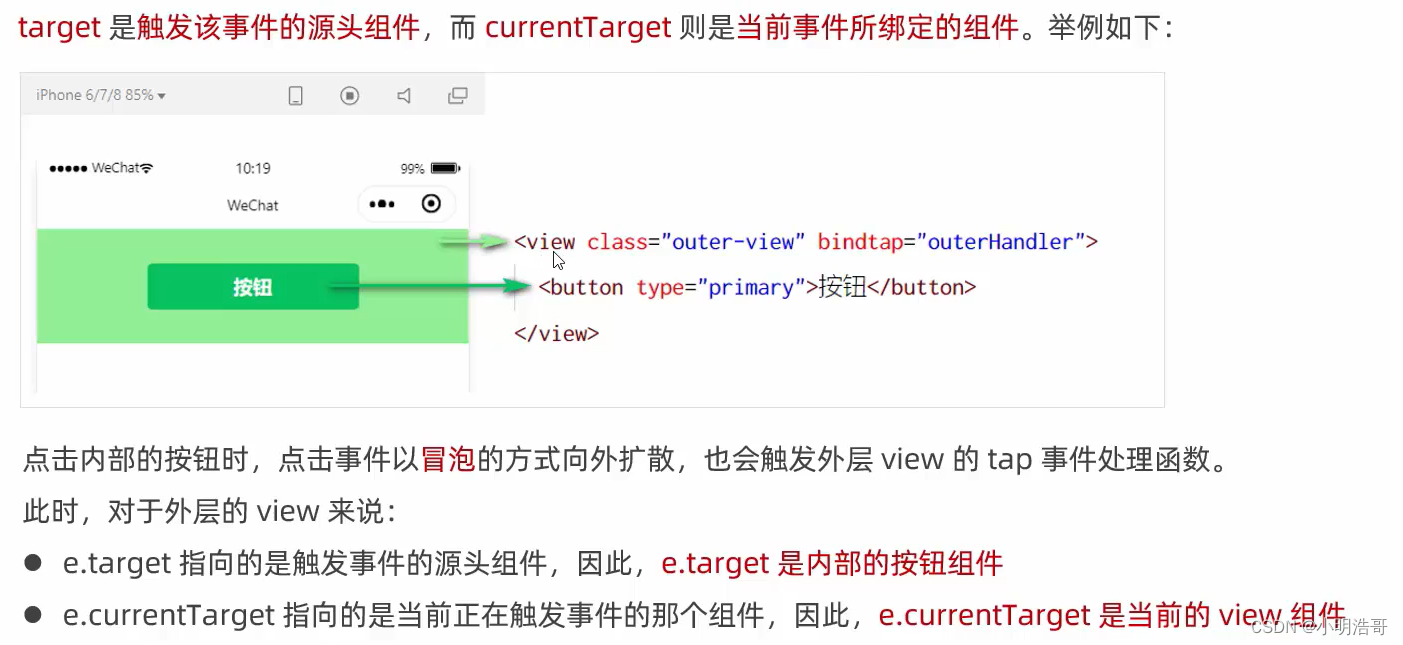
本系列所说的Mysql性能调优，主要是针对开发者在实际环境中的sql调优，代码层面上的优化。不涉及到mysql底层代码的调优。

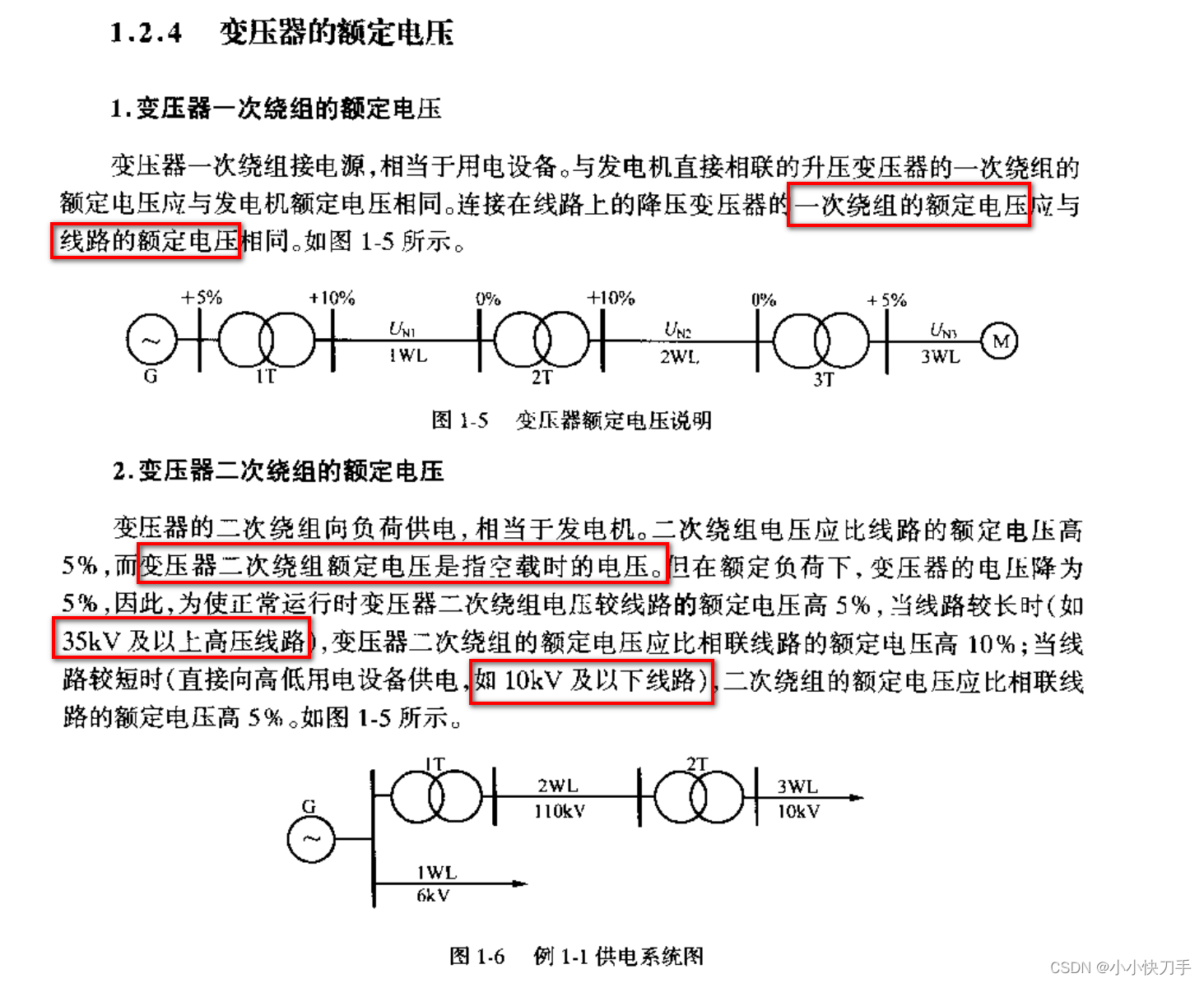
我们知道，一个mysql数据表，数据量小的时候，可能简单的查询耗时不会太久，性能也可以接受。但当数据量大的时候，查询速度会很缓慢。这时候我们会用到索引去优化查询。在我们的开发过程中，合理的索引对表操作的效率提升可能是指数级的。那我们在优化我们项目中的sql语句时，首要的就是基于索引原理进行优化。而要想有效率的，有针对性地进行mysql调优。必然要先了解其内部的一些知识，所以我们在这系列的第一篇要先聊一聊mysql索引的底层数据结构和算法。

---

一.什么是索引

可能我们之前听过，说索引就类似于字典的目录，或者类似书籍的目录，当你像查什么字可以根据拼音，偏旁部首等去定位到需要查看的页数，去获取相关的内容。这种说法不能说有错，但对于我们开发人员，这中层次的理解显然是远远不够的。至少你不可能就通过这个理解去做什么优化。因为这个没有说明白索引到底怎么回事儿。

先借用mysql官网的一句话来说：

•索引是帮助MySQL高效获取数据的排好序的数据结构

可能这个解释还是比较笼统，那接下来就让我们详细的研究一下索引到底是什么。

索引的数据结构

1. 二叉树
2. 红黑树
3. B-Tree
4. B+Tree

这里我罗列出来了上述的几种常见数据结构，大家应该都很熟悉了，我们再稍微的聊一下。比如说我们有如下的一个数据表：

这个表包含两列，一共7条数据。现在比如说我这里有一条sql语句

select * from test where col2 = 89

在不创建索引的情况，它应该就是走的所谓的“全表”。说白了就是从第一条逐次比对。第一个col2=34不对就下一个col2=77，一直到第6条，发现col2=89，那满足条件了将这条记录取出来，然后再继续查找。我们知道，数据库表中的数据是存储在磁盘当中的，而且这个存储位置也并非是绝对连续的（可能有连续的情况）。而当我们去磁盘中去读取一条数据，就是说做一次I/O读取交互的时候，这个效率是不高的。那当我们数据量大的时候，还使用这种全表扫描，每一条数据都要进行一次读取，这个效率是我们绝对接受不了的。那怎么避免这种情况呢？

最简单的，我们可以想办法减少查找次数。就是说，比如这里要的col=89这条数据，我们想办法不要去全表去扫描，不要逐行的去读取数据然后比对，以减少和磁盘做I/O读取操作的次数，从而提高我们的效率。那怎么做呢？这时候我们的索引就来了。我们可以给col2这列建一个索引，以达到我们想要的目的。

首先我们来看一下二叉树，如上图右侧部分，我们以二叉树的方式，建立col2这一列的索引。二叉树我们都知道的，右侧大于父节点，左侧小于父节点。上图中，我们二叉树根节点为表中第一条数据的col2值，为34。这个二叉树每个节点的结构就是key-value的。key就可以存的col2的每条的对应值，value可以是这条记录的存储地址。比如上图，34对应的数据地址就是0x07这样。当建立好这个索引后，再看我们最初的sql语句，这时候，你发现它走索引后，第一个扫描根节点即34那里，发现我们要找的89大于这个节点，那ok，直接向右查询，发现是89，直接取出这个值。就我上面这个例子，你发现不建立索引的时候，至少是要扫描6次才能找到col2=89这条数据，而走了二叉树结构的索引后，2次就找到了。这里效率可以说提升了很多。之前至少要和磁盘进行6次I/O读取，而现在只需要2次。这就是索引，详细到现在我们对索引的理解应该是要比“书籍目录”深刻一点儿了。但我们都知道，MySQL使用的并不是二叉树作为索引的数据结构。至于为什么，让我们想一下这样一个问题。

现在呢，我们更改一下我们的查询sql语句，改为用col1这一列来查找，如下：

select * from test where col1 = 6

现在要查询的还是col2=89的这条数据，但我们用col1=6来查找。这时候，基于上次的经验，我们要给col1创建一个索引，好的，一个二叉树索引创建完了。这个索引是什么样的的呢。大概是下面这样的：

因为二叉树的右侧永远大于父节点嘛，那当第一个数据也就是根节点的col1=1时，数据结构会如上图，这时候，想一下我们的语句，当走索引的时候，你发现，完了！又是需要查询6次才能获取到我们想要的数据。那这种情况如果数据量大的话，效率肯定也很低下，这可能也就是MySQL没有使用二叉树作为索引数据结构的原因。那我们怎么能优化一下呢？

这里我们可以使用红黑树进行优化，红黑树详细很多人都听说过，为了更直观了解它和单纯的二叉树的区别，我们可以看一下下面这个动图，这个展示了基于我们col1这个例子建立红黑树是什么样的：

你会发现，这个红黑树会根据数值的不同去平衡数据节点，其实红黑树就是一种特例的二叉树，它还是属于二叉树的，只不过加了平衡算法，但它又不能完全的称之为“平衡二叉树”，因为它的左右可以是高度不同的，平衡二叉树是另一种叫做AVL树的数据结构，感兴趣可以自己去查一下，这里就不多说了。说会我们的例子，当我们将原来的二叉树换成红黑树后，会发现现在查询到我们想要的数据只需要三次查询，较之前的纯粹二叉树结构有了一些性能上的提升。尽管如此，我们也都知道MySQL用的也不是红黑树。因为这样的平衡二叉树，或者说红黑树，仍然有一些问题。比如说，我上边的例子是因为只有七条数据，数据量很少，我们可以接受。但当数据量达到百万级别，千万级别的时候。我们平常的生产环境这个数据量很容易达到的。这个时候，红黑树的性能就没有那么高了，说白了就是它有一个“树高”的问题，当数据量很大的时候，当我们查找的数据在叶节点上时候，可能要查询很多次，几十次，因为虽然红黑树做了平衡，但随着数据量的增加，它的“树高”也在不停的增长。当我们查一条数据的时候要和磁盘交互几十次的时候，那这个性能就明显不够了。红黑树也就无法满足我们的需求了。好的，那我们继续优化，针对这种“树高”的问题，我们怎么处理呢？

其实通过上面的二叉树和红黑树，我们应该已经感觉到了，就是我们和磁盘的交互次数，或者说我们查询数据的次数，和“树”的高度是紧密相关的。那如果我们能让上边的红黑树或者说二叉树的树高，不管是存几百万还是几千万数据的时候都能保证树高在3、4层的话，这个我们和磁盘交互的次数，感觉我们还是可以接受的。性能就会相对较高一些。那怎么做呢？

我们想想一下，既然想减少树的纵向高度，那是不是可以在横向上想想办法。我们知道，这个树的每个节点，或者说索引的的节点也是存在磁盘上的。比如说上面红黑树的根节点“1”这个值，可能占用了磁盘的一个存储空间。那我们能不能在生成树的时候，直接让每个节点的存储空间扩大一些。就比如，在第一层，我现在可以存多个索引值。7个值的话，我们看红黑树是有三层，如果可以将每一层的每个节点多存储几个元素，比如说我这里设置成每个节点最多4个。整个存储过程就如下：

这种优化后，发现7条数据只需要存两层，如果我将每层设置做多可存值大于7，那就只需要一层。相对红黑树，性能应该就是又有一些提升了。而这种数据结构，就是B-Tree。为了更形象一点儿，我们再看一下下图：

上图为大致的B-Tree数据结构，其中15、56、77等可以理解为索引字段的值，而data则为对应那条记录的数据，或者说存储地址。我们观察B-Tree结构，发现它有如下几个主要特点：

• 叶节点具有相同的深度，就是说不会像红黑树一样分支的深度不一致。
• 所有的索引元素不重复的
• 节点中的数据索引从左至右递增排序

虽然B-Tree一定程度上解决了“树高”的问题，但我们知道MySQL用的是叫做B+树的数据结构，那接下来我们就看看它和B树的区别，再研究一下MySQL为什么要使用B+树。首先就我们的例子，生成一个B+Tree，看一下什么样子的:

好像粗略看去，和B-Tree很相似。没错，本来B+Tree就是B-Tree的变种，这里我们注意上面动图中，叶节点中间的那个指示箭头。这个东西代表叶节点是有存相邻节点的相关信息的，就是节点的中可能有一小块存储空间放的是相邻节点的存储地址，这样的话，方面直接快速查到相邻节点和排序等。我们再看下面的图片：

看这张图片，和B-Tree很明显的结构，你会发现除了最下层的叶节点中含有data信息，上面的每一层，包括根节点，都没有存储数据，只是存了索引值。那我们可以知道，最后的叶节点中是包含所有索引值和data的。说白了，就是最下一层叶节点中包含上面所有层的索引值，而且是从左到右逐次递增的，并且节点之间存有相邻节点的信息。这时候其实上部分的节点存的就是“冗余索引”。那Mysql为什么要在B-Tree上做这种变更呢？

二.Mysql的索引

我们都知道，数据表包括索引都是存储在磁盘上的，比如MySQL如果你不更改安装配置的话，一般到它的安装目录下就能找到每个表对应的数据文件。

那是不是有这样一个问题，就像上面的B+Tree，虽然在每个节点中存储了多个索引值，减少了树高，但我查找的时候不是还要和磁盘交互么，不是还要去一条一条比对么？那这个磁盘I/O不是还是很慢么？没错，如果是直接去磁盘进行读取操作的话，那是这样的。但MySQL是这么做的：首先我们从根节点来说起，就是刚开始查询的时候，它会把整个根节点读入到RAM中，说白了就是将磁盘中的节点信息，读到内存中，然后在内存中做查询。其中会用到一些算法，比如““折半法”,也就是二分查找等。当在内存中做这种查找的时候，效率是十分快速的。甚至和磁盘读取来比较的话，这个时间消耗甚至是可以忽略不记的。我们举个例子，比如说我们上面的那个B+Tree图片，一共3层，当我查找索引值为20这一记录的时候，它的查找过程大概是这样的：首先根节点从磁盘中读到内存中，然后运用二分法快速的查到20这个值所在的下一层存储位置，然后再将对应的节点整个读取到缓存中，再进行查找，最终查到我们要的值所在位置，然后读取出来。那其实我们主要耗时的地方还是和磁盘交互的过程，在这里就相当于把节点数据读取到内存中这个操作。一共就是有3次的I/O读取。这个效率就很高了。我们的例子数据比较少，可能没有直观的感受，那我们计算一下。

首先我要说的是当你用MySQL时，运行如下语句：

SHOW GLOBAL STATUS like 'Innodb_page_size';

你会得到一个值，默认应该是16K，这个值是什么呢？它代表的就是每个节点的存储空间大小。就是文件页，或者说磁盘页。这个东西用根节点来说，就是这个节点的空间是16K。我们想一下，就假设一行数据1K大小（一般表格一条数据达不到），那在最下一层的叶节点中，每个节点可以存16条数据。好的，那上层我们假设我们建立主键索引的字段为ID列，算大一点bigInt类型，bigInt在MySQL中大小为8B，指针在Innodb源码中大小是6B，一共为14B。那么一页就是16K/14B = 1170（主键加指针）。如果我们这个B+Tree有3层，那数据总量就是1170117016 = 21902400。现在是不是很直观了，千万级别的数据，使用Innodb类型的表格，使用索引只有3层，这时候想一下千万级别我们走索引查询的话，只需要进行3次I/O读取操作！这就是为什么MySQL可以千万级别查询做到毫秒级别。

说到这里，那我们再想一下为什么B-Tree不行。想一下，B-Tree是每个索引后都跟着数据的，那以根节点来说，如果同样是16k的大小，B+Tree可以存1170条，而B-Tree只能16条。当数据量大的时候，树又会很高了。还一个问题是，可能会想那我们把文件页大小分配大一点不就好了，但有个问题，如果这个值大了，B-Tree虽然每个节点中的索引量可以存储的更多了，但是由于文件页很大，这时候如果像B+Tree一样将其读取到内存中操作，显然就不合适了。将及其耗费资源。如果不读取到内存，那处理速度依然很慢。这就是为什么Mysql要将B-Tree变种从而得到B+Tree。

好了，本篇就先聊到这里吧，还有很多点没有说到，下一篇再结合Mysql展开详细说一下，然后再说一些优化方法，这篇文章是要我们对B+Tree有个深入了解。因为后边索引优化，都是基于这个结构的。脑袋中有这个结构，会省力很多。

下篇会聊一下mysql的存储引擎，主要是Innodb。