什么是树

相信大家刚学数据结构的时候最先接触的就是顺序表,栈,队列等线性结构.
而树则是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合

非线性 体现在它是由n个有限结点(可以是零个结点)组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的
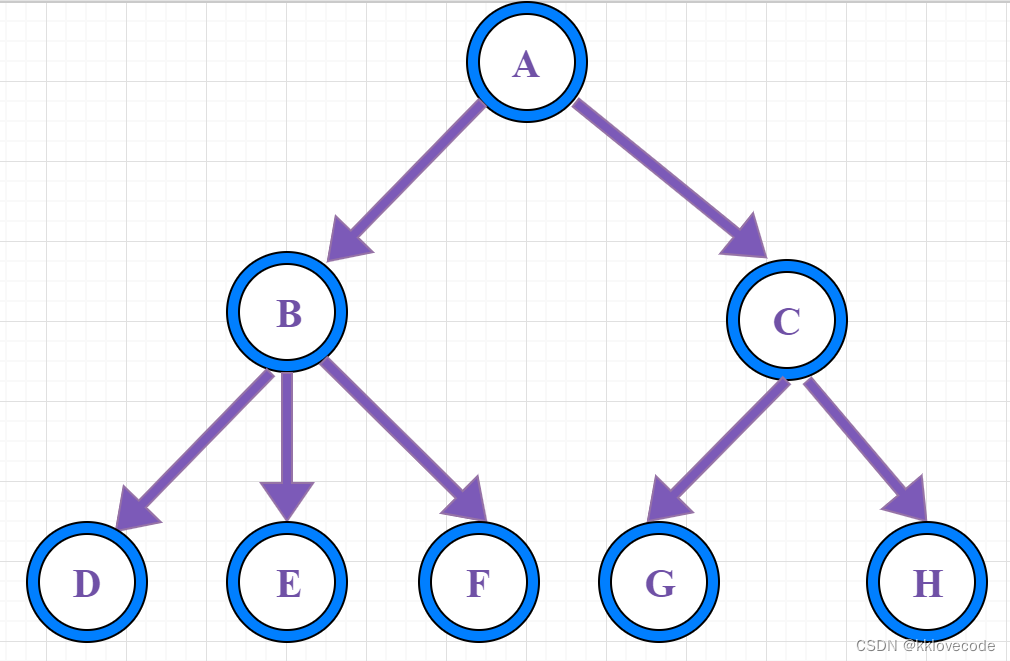
一对多 体现在比如对图中A来说,A对于和B,C都存在联系,同理B,C与其他的也均存在关系

树的常见术语

节点的度：一个节点含有的子树的个数称为该节点的度(上图A的为2)
叶节点/终端节点：度为0的节点称为叶节点(上图DEFGH节点为叶节点)
非终端节点/分支节点：度不为0的节点,(上图A,B,C)
双亲节点/父节点：若一节点含有子节点,此节点称为其子节点的父节点(上图A是B的父节点)
孩子节点或子节点：一节点含有的子树的根节点称为该节点的子节点(上图B是A的孩子节点)
兄弟节点：具有相同父节点的节点互称为兄弟节点(B、C是兄弟节点)
树的度：一棵树中,最大的节点的度称为树的度(上图B的度最大,故树的度为3)
堂兄弟节点：双亲在同一层的节点互为堂兄弟(如上图D,E互为兄弟节点)
节点的祖先：从根到该节点所经分支上的所有节点(上图A是所有节点的祖先)
子孙：以某节点为根的子树中任一节点都称为该节点的子孙(上图所有节点都是A的子孙)
森林：由n(n>0)棵互不相交的树的集合称为森林

此外,另有两个术语需要单独讨论一下,即

节点的层次：从根开始定义起，有两种说法
①根为第1层，根的子节点为第2层…
②根为第0层，根的子节点为第1层…
树的高度或深度：树中结点的最大层次

---

---

比如,只有一个节点,A是第0层,也可以说是第1层,两者都是正确的
但是我更推荐说A是第1层,因为如果A是第0层,高度或深度就为0,
那么对于空树来说,它就只能是-1层,显然不合理
那么如果A是第1层,高度或深度就为1;而空树的高度或深度就为0了,个人认为这种安排更加合理

---

---

树的表示

树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等.

首先我们来看一种比较差的表示

struct TreeNode
{int val;struct  TreeNode* child1;struct  TreeNode* child2;struct  TreeNode* child3;//...
};    //缺点很明显,浪费空间,对于度只有1或0的节点就会浪费结构体内的空间//或者稍微改进一下
struct TreeNode
{int val;struct  TreeNode* childArray[5];
};  //同理,如果没有5个孩子的节点也会浪费空间

现在介绍一种非常常用且厉害的方法: 孩子兄弟表示法

struct TreeNode
{int val;struct  TreeNode* firstChild;struct  TreeNode* brother;
};    

此方法的思路流程如下:(链表)

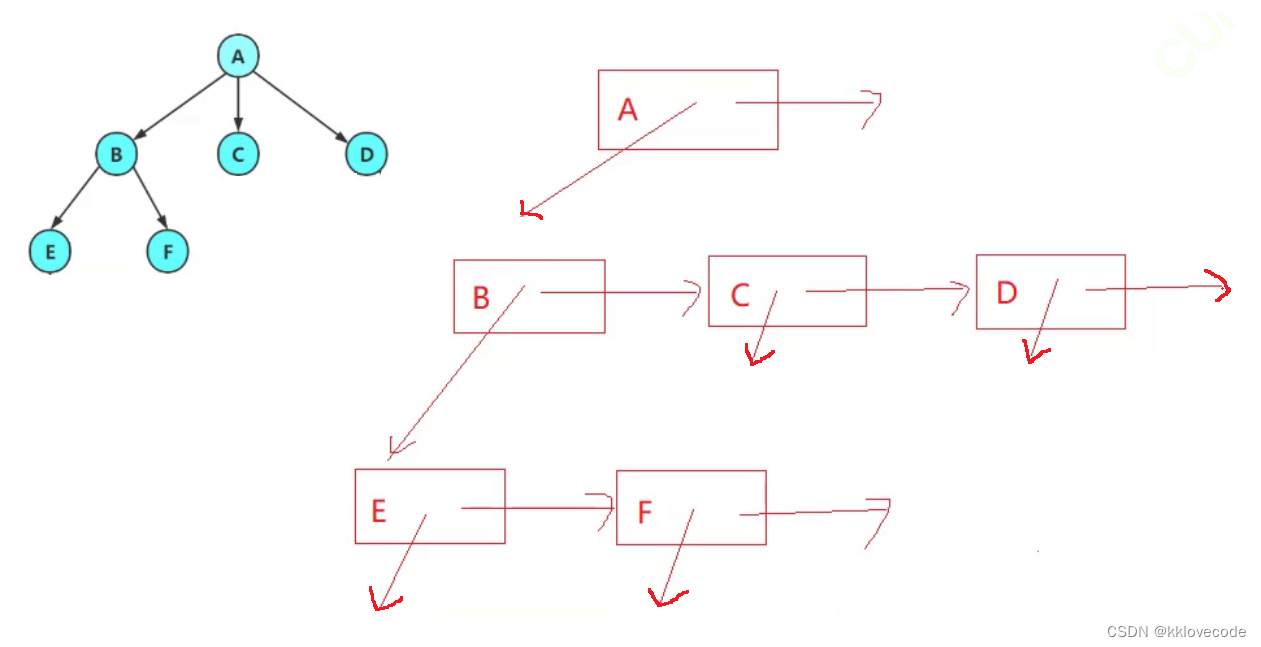
再比如 双亲表示法:只存在父亲节点的指针或者下标

#define size 100//树中结点的最大数量
#define dataType int//树结构中数据类型
//节点
typedef struct TreeNode{dataType data;//树中结点的数据类型int parent;//它的父结点在数组中的位置下标
}TreeNode;
//树结构:  (上面的方法没有写这个树结构是因为上面是本质是链表,而这里是数组)
typedef struct {PTNode nodes[size];//存放树中所有结点int r,nums;//根的位置下标和结点数
}Tree;

逻辑思路如下(数组)

树的应用

1.文件系统：计算机的文件系统通常采用树形结构来组织文件和目录。根节点是文件系统的根目录，每个目录可以包含子目录和文件，这种结构可以方便地组织和访问文件。
2.数据库索引：数据库中的索引通常使用B树或B+树这样的树形结构来实现。树的节点包含关键字和指向其他节点的指针，可以快速地搜索和访问数据库中的数据。
3.解析树：编译器常使用树形结构来表示程序的语法结构。每个节点代表一个语法规则或语句，子节点表示该语句的组成部分，这种结构可以方便地进行语法分析和代码生成。

注:这只是树形结构在实际中的一部分应用，它的灵活性和易于理解性使其成为许多领域中常用的数据结构。