目录
题目:
示例:
分析:
代码:
题目:
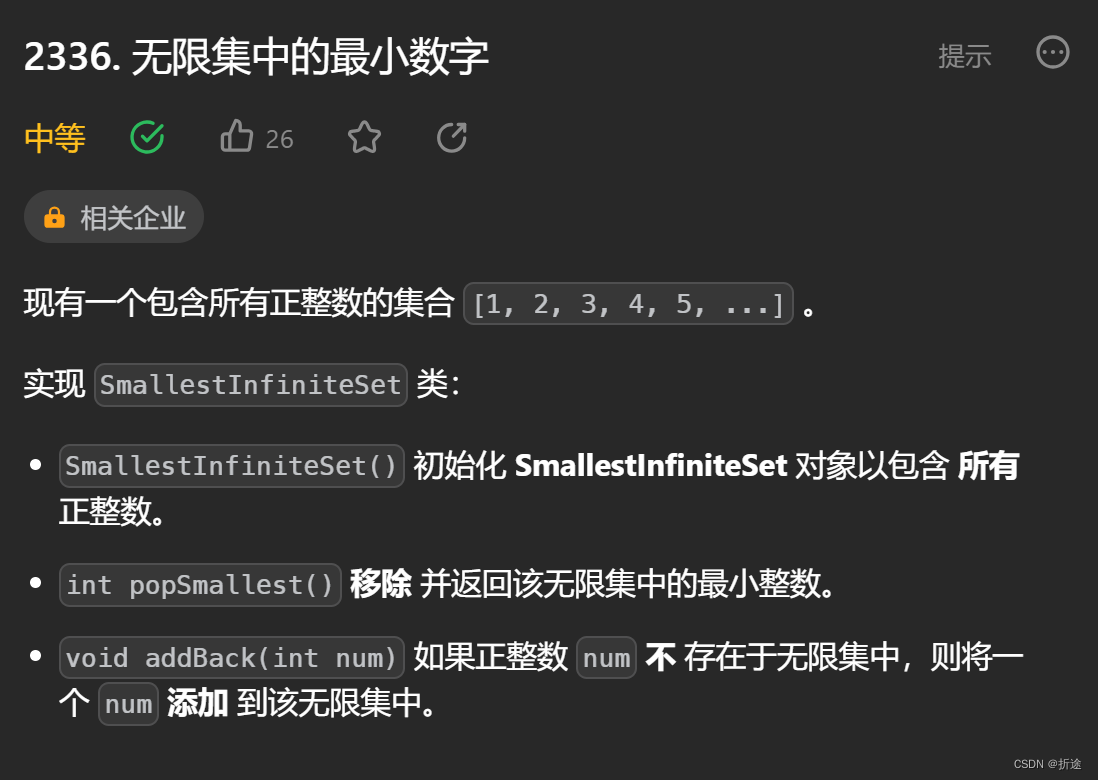
示例:

分析:
这是我们在LeetCode75里遇到的第二道设计类题目,难度比上一次的设计题目要难上一些。
题目假设我们拥有一个从1开始的无限集。
设计的这个类有两个调用函数,一个让我们将无限集中最小的数移出并返回,另一个函数让我们再将一个不在无限集里的数添加会无限集里。
那么题目有给出条件,重新加回无限集的数不会大于100,并且调用次数的总和不会超过1000次。
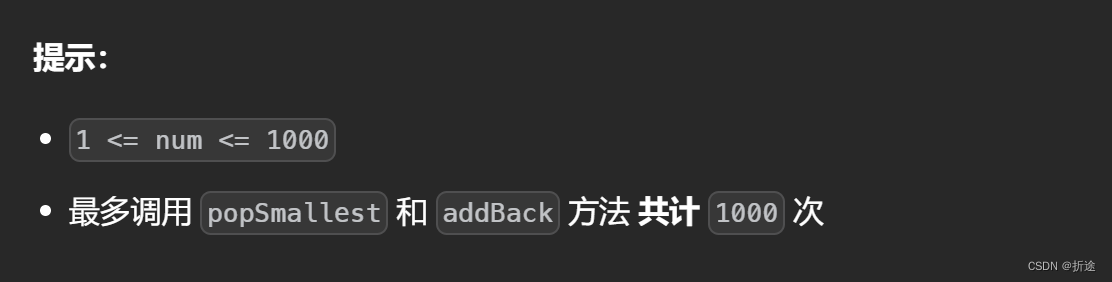
那么我们可以直接拿一个数组来存放1000个数字来模拟无限集,因为就算1000次调用的都是移除最小值,那么1000个数字也是刚好够移除的。
不过这仅仅是理论可行,因为直接模拟的话,是会超时的。
我们可以逆向思考一下,我们不存放存在无限集的数字,我们存放被移出无限集的数字。
并且我们使用set来存放,这样每次移除最小数的时候,我们从1开始寻找set,如果数字不在set里,那么我们就把数字加入到set里来表示这个数被我们移除了。
添加回无限集的时候就更简单了,我们直接寻找要添加的数在不在我们的set里,如果在,我们就把set里的这个数字移除来表示添加回无限集里,因为set里存放的是被移出无限集的数,这样可能有点绕,大家结合着下面的代码再捋一捋。
代码:
class SmallestInfiniteSet {
public:unordered_set<int>jihe; //存放的实际上是被移出无限集的元素SmallestInfiniteSet() {}int popSmallest() {int i=1;while(jihe.find(i)!=jihe.end()){ //从1开始寻找没有被移出无限集的数,第一个找到的就是最小数i++;}jihe.insert(i); //找到之后插入set表示该数被移出无限集return i;}void addBack(int num) {//如果该数在set里,也就是被无限集移出了,那么我们再将其移出set表示重新加回无限集里if(jihe.find(num)!=jihe.end()){ jihe.erase(num);}}
};