目录
算法
评价标准
时间的复杂度
概念
推导原则
举例
空间的复杂度
定义
情形
运用场景
数据结构
组成方式
算法
在数学领域,算法是解决某一类问题的公式和思想;
计算机科学领域,是指一系列程序指令,用于解决特定的运算和逻辑问题;
评价标准
衡量算法好坏的重要标准是:时间复杂度和空间复杂度;
代码运行时间的长短和占用内存空间的大小,是衡量程序好坏的重要因素。
时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间
时间的复杂度
概念
计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间
推导原则
如果运行时间是常数量级,则用常数1表示
只保留时间函数中的最高阶项
如果最高阶项存在,则省去最高阶项前面的系数
举例
例1:给小灰1个长度为10cm的面包,小灰每3分钟吃掉1cm,那么吃掉整个面 包需要多久?
答案是:3×10即30分钟。
如果面包的长度是n cm呢?
此时吃掉整个面包,需要3乘以n即3n分钟。
如果用一个函数来表达吃掉整个面包所需要的时间,可以记作T(n) = 3n,n为面 包的长度
例2:给小灰1个长度为16cm的面包,小灰每5分钟吃掉面包剩余长度的一半, 即第5分钟吃掉8cm,第10分钟吃掉4cm,第15分钟吃掉2cm……那么小灰把面包吃得 只剩1cm,需要多久呢?
把面包吃得只剩下1cm,需要5×log16即20分钟。
如果面包的长度是n cm呢?
此时,需要5乘以logn即5logn分钟,记作T(n) = 5logn。
设T(n)为程序基本操作执行次数的函数,n为输入规模,刚才的2个场景分别对应了程序中最常见的2种执行方式:
例1中:T(n) = 3n,执行次数是线性的;最高阶项为3n,省去系数3,则转化的时间复杂度为:T(n)=O(n)。

例2中:T(n) = 5logn,执行次数是用对数计算的;最高阶项为5logn,省去系数5,则转化的时间复杂度为:T(n) =O(logn)。

渐进时间复杂度用大写O来表示,所以也被称为大O表示法
空间的复杂度
在运行一段程序时,我们不仅要执行各种运算指令,同时也会根据需要,存储 一些临时的中间数据,以便后续指令可以更方便地继续执行。
定义
是对一个算法在运行过程中临时占用存储空间大小的量度;空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
情形
1.常量空间:当算法的存储空间大小固定,和输入规模没有直接的关系时,空间复杂度记 作O(1)。
2.线性空间:当算法分配的空间是一个线性的集合(如数组),并且集合大小和输入规模n成 正比时,空间复杂度记作O(n)。
3.二维空间:当算法分配的空间是一个二维数组集合,并且集合的长度和宽度都与输入规模n 成正比时,空间复杂度记作O(n 2 )。
4.递归空间:递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或集合, 但是计算机在执行程序时,会专门分配一块内存,用来存储“方法调用栈”。
运用场景
1.运算
2.查找
3.排序
4.最优决策
数据结构
是数据的组织、管理和存储格式,其使用目的是为了高效的访问和修改数据
组成方式
1.线性结构:最简单的数据结构,其中包括了数组、链表、以及衍生出来的栈、队列、哈希表

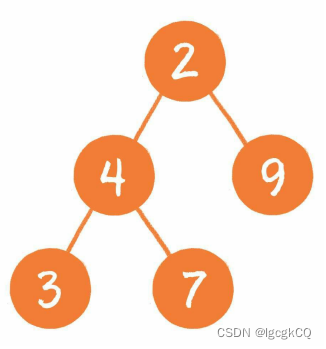
2.树:相对复杂的数据结构,其中有代表性的是二叉树,由它又衍生出二叉堆之类的数据结构
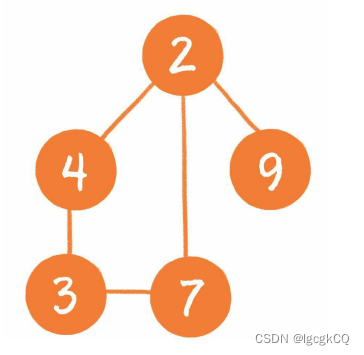
3.图:是更为复杂的数据结构,在图中会呈现出多对多的关联关系
4.其他数据结构:由基本数据结构变形而来,用于解决某些特定问题,如跳表、哈希链表、位图 等
注意:
有了数据结构算法才能尽情地发挥;在解决问题时,不同的算法会选用不同的数据结构