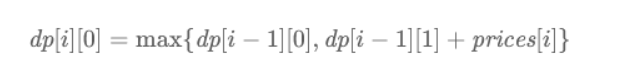1、题目:
给你一个整数数组 prices,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持一股股票。你也可以先购买,然后在同一天出售。
返回你能获得的最大利润 。
2、分析特点:
- 题目要求:在任何时候最多只能持一股股票 ==> 考虑到「不能同时参与多笔交易」,因此每天交易结束后只可能存在手里
有一支股票或者没有股票的状态。 - 有和没有股票的状态 ==> 动态规划
定义状态dp[0] 表示第天交易完后手里没有股票的最大利润,d[1] 表示第天交易完后手里持有一支股票的最大利润(从0开始)。
考虑dp[i][0] 的转移方程,如果这一天交易完后手里没有股票,那么可能的转移状态为前一天已经没有股票,即 dp[i-1][0], 或者前一天结束的时候手里持有一支股票,即 dp[i-1][1],这时候我们要将其卖出,并获得 prices[i] 的收益。 因此为了收益最大化,我们列出如下的转移方程:
再来考虑dp[i][1],按照同样的方式考虑转移状态,那么可能的转移状态为前一天已经持有一支股票,即 dp[i-1][1],或者前一天结束时还没有股票,即 dp[i-1][0],这时候我们要将其买入,并减少prices[i]的收益。可以列出如下的转移方程:
对于初始状态,根据状态定义我们可以知道第0天交易结束的时候 dp[0][0] =0,dp[0][1]=-prices0。 因此,我们只要从前往后依次计算状态即可。由于全部交易结束后,持有股票的收益一定低于不持有股票的收益,因此这时候 dp[n-1][0] 的收益必然是大于 dp[n-1][0] 的,最后的答案即为dp[n-1][0]。
3、特点:
本题动态规划法的思路解析:
因为,从最后一天往前看,分成四种情况:
A:前一天有股票,并卖出 – 剩余股票数0
B:前一天没有股票,并不买入 – 剩余股票数0
C:前一天有股票,并不买出 – 剩余股票数1
D:前一天没有股票,并买入 – 剩余股票数1
所以:
- 当剩余股票数0时,最大的利润是max(A, B)
- 当剩余股票数1时,最大的利润是max(C, D)
4、代码:
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);}return dp[n - 1][0];}
}
注意到上面的状态转移方程中,每一天的状态只与前一天的状态有关,而与更早的状态都无关,因此我们不必存储这些无关的状态,只需要将 dp[i-1][0]和dp[i-1][0] 存放在两个变量中,通过它们计算出dp[i][0] 和 dp[i][1] 并存回对应的变量,以便于第 i+1 天的状态转移即可。
4、复杂度分析:
- 时间复杂度:O(n),其中 nnn 为数组的长度。一共有 2n 个状态,每次状态转移的时间复杂度为 O(1),因此时间复杂度为 O(2n)=O(n)。
- 空间复杂度:O(n)。我们需要开辟 O(n) 空间存储动态规划中的所有状态。如果使用空间优化,空间复杂度可以优化至 O(1)。
5、总结:
本题动态规划法的思路解析---有股票和没股票结合买入卖出的情况考虑状态
因为,从最后一天往前看,分成四种情况:
A:前一天有股票,并卖出 – 剩余股票数0
B:前一天没有股票,并不买入 – 剩余股票数0
C:前一天有股票,并不买出 – 剩余股票数1
D:前一天没有股票,并买入 – 剩余股票数1
所以:
- 当剩余股票数0时,最大的利润是max(A, B)
- 当剩余股票数1时,最大的利润是max(C, D)
如果本文对你有帮助的话记得给一乐点个赞哦,感谢!